专业论文|基于Abaqus和Isight的涡轮叶片燕尾榫几何设计研究
▲专业论文|基于Abaqus和Isight的涡轮叶片燕尾榫几何设计研究
本文作者:禹燕飞 张伟
达索析统(上海)信息技术有限公司北京分公司
本文利用Abaqus和Isight软件对典型涡轮叶片燕尾榫周围的接触压力和应力进行了优化设计研究,以达到理想的应力水平。首先通过Python脚本设置描述燕尾榫尺寸的9个设计参数,在Abaqus/CAE中生成整个有限元模型。然后在考虑离心载荷的前提下进行了非线性静力分析。基于Isight优化平台搭建工作流,实现了分析流程的自动化,以获得优化的燕尾型尺寸。优化分两步进行。首先,基于Isight使用DOE技术采集设计样本创建代理模型,使用代理模型确定设计变量的最优值,以及设计对所选设计变量的灵敏度。其次,根据分析结果对设计变量进行精简并进行第二步优化。两级优化中均使用了Isight支持的几种不同的优化方法,包括NSGA-II非支配排序遗传算法、下山单纯形算法和进化优化算法等,并将这些方法的结果进行展示和对比。
Evol进化优化算法 NSGA-II第二代非支配排序遗传算法 RSM响应面模型 EBF椭球基神经网络模型 CPRESS接触压力

在燃气轮机和蒸汽轮机行业中,涡轮叶片是实现高可靠性和高效率的关键部件。如图1所示的涡轮叶片是通过叶片的燕尾榫或紧固件与叶轮中相应凹槽之间的接触相互作用与轮盘连接的。在正常工作条件下,接触区域通常是一个高应力区。许多研究者使用有限元分析方法,来预测在热载荷和结构载荷条件下叶片和轮盘装配的精确应力水平,用于叶片设计,然而,有限元分析本身并不足以提供优化设计。因此,除了有限元分析之外,还需要设计流程自动化和优化工具,以便在合理的时间内获得最佳的叶片设计。
本文利用有限元软件Abaqus 2020和过程自动化优化软件Isight 2020,对离心载荷作用下涡轮叶片和轮盘的燕尾榫进行了参数优化分析。为了有效地利用不同的优化算法得到优化结果,采用有限元模型及其近似模型(代理模型)进行两级优化,并将所得结果进行展示和讨论。
本文采用Abaqus/CAE软件建立几何模型和有限元模型。图1显示了叶片和轮盘装配的几何形状,该装配是通过组合翼型、护罩、平台和轮盘的零部件创建的,假设在平台和轮盘中,燕尾型榫头接触区的截面几何形状是相同的。

图1 叶片/轮盘组件的部分:护罩(左上),翼型(右上)
燕尾型平台(左下),轮盘(右下)
在Abaqus/CAE中创建叶片和轮盘装配的网格,轮盘采用C3D8和C3D6单元,其他所有部件均采用C3D4单元,如图2所示。轮盘与叶片之间的接触相互作用定义如图3左图所示,轮盘两侧的循环对称条件定义如图3中间图所示。本文假设护罩侧面不存在接触,在本研究中,只考虑离心载荷,轮盘的底部是固定的,作为边界条件,载荷和边界条件的定义情况如图3右图所示。本文只考虑非线性静力过程。
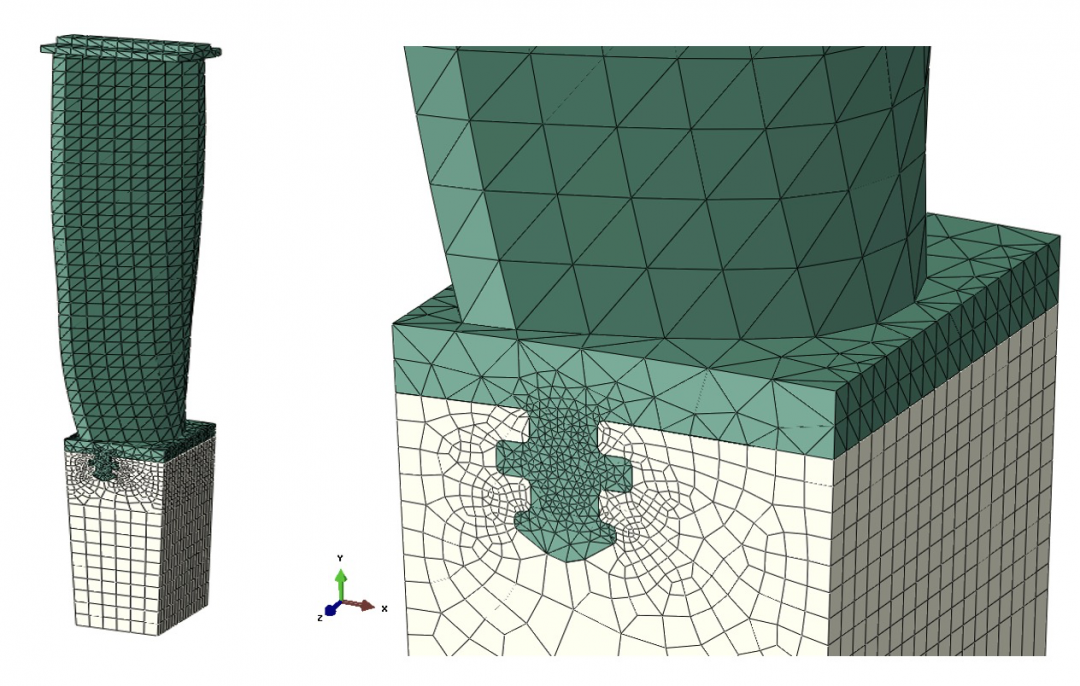
图2 叶片和轮盘的装配
(左:几何,中:网格,右:局部放大)
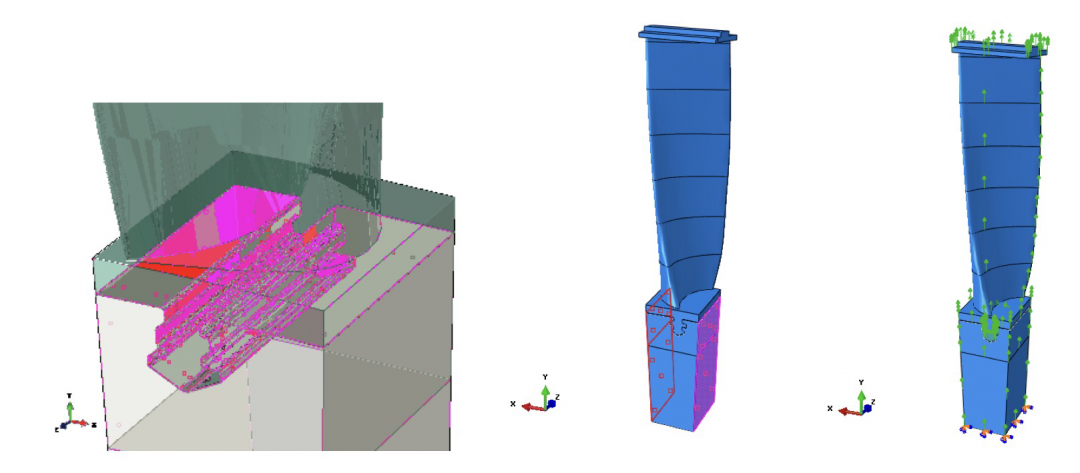 图3 左:叶片与轮盘接触作用;
图3 左:叶片与轮盘接触作用;
中:循环对称条件;右:载荷和边界条件
Isight能够利用仿真工具搭建复杂的设计流程,并通过“组件”实现自动化。Isight包括三类优化方法:1)梯度法,2)直接法,3)探索法。本文考虑了这三种类型的几种优化方法,如表1所示。
表1 本文选取的优化方法简介

本文采用两级优化方法。在第一级,首先进行试验设计运行,利用最优拉丁超立方采样技术对设计空间进行抽样,并创建近似模型,使用近似模型执行优化。然后基于试验设计结果进行灵敏度分析,以确定对应力最小化影响最大的设计变量。在构建代理模型时,本文考虑并比较了两种不同的代理模型(RSM和EBF),流程图如图4所示。
在第二级优化过程中,仅使用EBF模型在第一级优化中识别的最敏感的设计变量再次执行优化。在第二级优化,使用相同的优化方法进行设计评估,流程图如图5所示。

图4. 第一级流程图

图5. 第二级流程图
燕尾榫的横截面形状以及设计变量的初始值及其允许范围(即约束)如图6所示,假设燕尾榫的截面形状对称,所有尺寸单位均为mm。
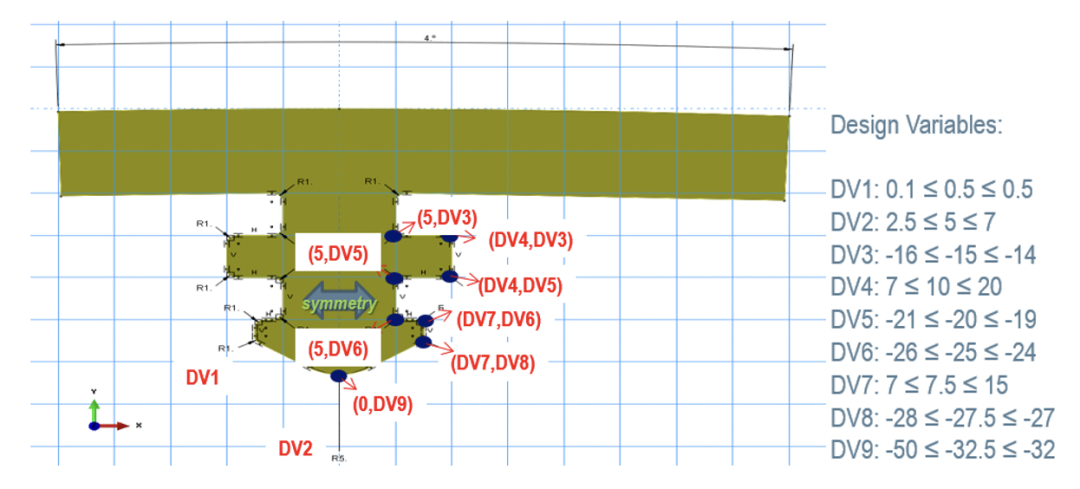
图6. 对设计变量初始值和约束条件进行一级优化
在第一级优化中选择指定燕尾榫截面尺寸的所有9个设计变量(DV1到DV9),以优化(即最小化)燕尾榫周围的接触压力和von Mises应力。表2显示了采用不同优化方法的两种代理模型对各设计变量的优化值,CPRESS和Mises分别代表接触压力和von Mises应力。
表2 使用一级优化近似模型计算的接触压力
和von Mises应力
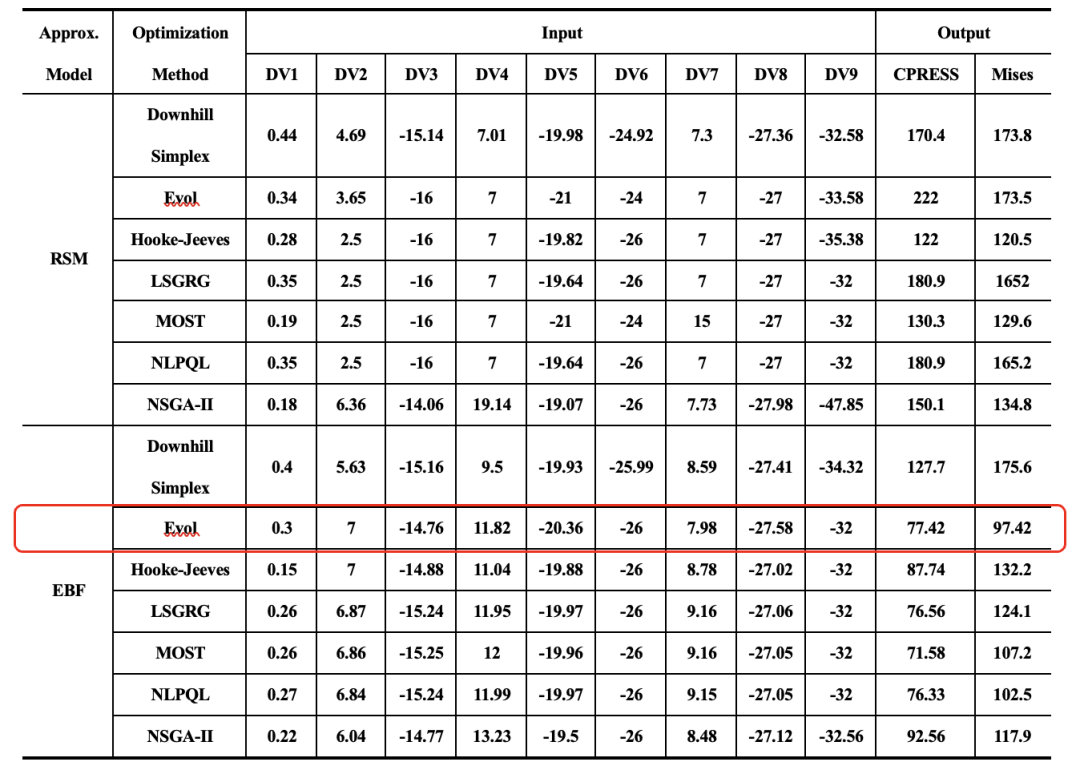
结果表明,与响应面模型相比,EBF模型的接触压力和von Mises应力值更低,效果更好。同样是采用EBF代理模型,Evol优化方法得到的整体结果优于其他优化算法。NSGA-II方法在两种代理模型中均得到了相对较小的接触压力和von Mises应力结果。下山单纯形法得到的结果最差,但所有梯度法都能得到很好的结果。
观察EBF代理模型的结果,可以很容易地看出设计变量DV5、DV6、DV8、DV9的值在不同的优化方法下没有太大变化。因此,将这些设计变量的值设置为常量。由于采用EBF模型的Evol优化方法可获得最佳结果,因此设计变量DV5、DV6、DV8和DV9的值被设置为该结果中发现的值的常量,以便在下一级优化中与EBF模型一起使用。其余设计变量的初始值被设置为EBF模型中使用Evol方法获得的最优值。
表3显示了第二级优化的初始值(蓝色单元格),以及各种优化方法的第二级优化结果(黄色单元格显示设置为常量的设计参数)。
表3. 第二级优化的初始值及优化结果

通过比较表2和表3的结果,可以发现基于梯度的方法并不能提供比EBF代理模型得到的结果更好的解决方案。特别是LSGRG和NLPQL,结果与初始起点相同。但是,如表3所示,直接法和探索法可以提供改进的结果。
尽管不同的优化方法得到的结果略有不同,但由于优化目标是接触压力或von Mises应力最小,因此有三种结果可以被视为优化设计:
1) 第一级优化中使用Evol方法得到的结果
2) 第二级优化中使用Evol方法得到的结果
3) 第二级优化中使用NSGA-II方法得到的结果
图7显示了原始设计和上面选定的两个优化设计的循环对称叶片模型中von Mises应力和接触压力云图。大多数情况下,最大压力和von Mises应力位于相似的位置。图8显示了在离心力作用下循环对称模型变形形状下的接触压力和接触间隙。

(a) 原始设计 CPRESS:162.1, von Mises:142.6
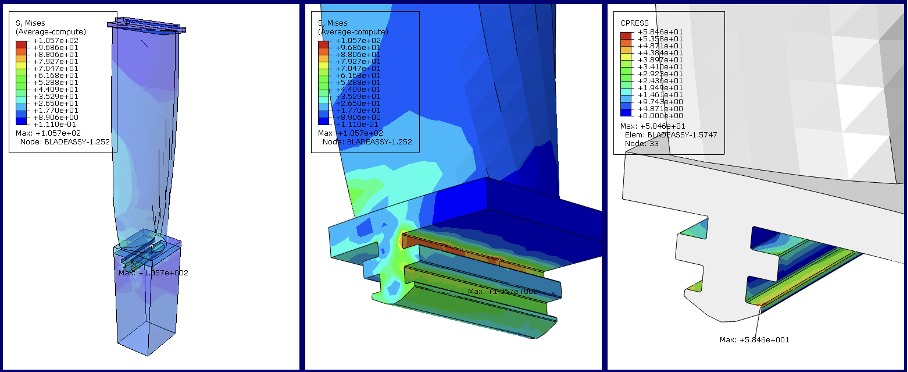
(b)第二级优化采用Evol优化方法进行优化设计
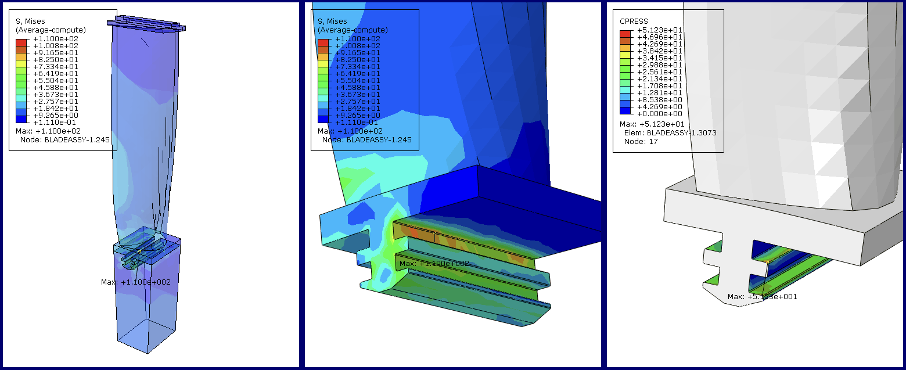 (c)第二级优化采用NSGA-II方法进行优化设计
(c)第二级优化采用NSGA-II方法进行优化设计
图7. 原始设计与优化设计结果比较

图8. 接触压力和间隙
本文采用多种优化方法对涡轮叶片的燕尾榫截面进行了优化设计。结果表明,两级优化方法与代理模型相结合,可以提供一种更稳健的设计方法。利用代理模型进行了一级优化分析,并选取主导设计变量。第二级优化分析是利用主导设计变量和多种优化方法进行的。在所尝试的优化方法中,NSGA-II遗传算法和Eovl进化方法提供了最佳的解决方案。
-END-





