基于颗粒离散元PFC的圆盘刀具破岩过程声发射矩张量模拟
基于颗粒离散元PFC的圆盘刀具破岩过程声发射矩张量模拟
本文摘要(由AI生成):
本文研究了岩石切削过程中刀具-岩石相互作用应力,利用离散元方法(DEM)和颗粒离散元PFC编程声发射矩张量代码对刀盘破岩过程进行模拟。建立了圆盘刀具破岩的数值模型,并通过矩张量分析程序分析了试样在刀盘作用下的声发射信号。模拟结果包括震级分布、不同类型裂纹空间分布图和声发射特征分析。结果表明,该模型能够较好地模拟岩石切削过程,有助于理解刀具-岩石相互作用机制和岩石破碎机制。
1. 引言
隧道掘进机(TBM)在隧道工程中被广泛采用,因为它为工作人员提供了安全的工作环境,在不利的地质条件下效率高,地面扰动小。然而,由于TBM操作的复杂性和地质条件的不确定性,TBM刀盘和开挖面之间的相互作用仍然是一个尚未得到充分理解的关键问题。通常,刀盘和开挖面之间的相互作用可以简化为刀盘上的圆盘刀具和开挖面上的岩石之间的相互影响。在过去几十年中,通过实验室切割试验和数值模拟原位监测研究了刀盘相互作用。刀具-岩石相互作用力由三个分量组成:垂直于岩石表面的法向力、沿切割方向的滚动力以及垂直于切割方向和法向力方向的侧向力。刀具与岩石的相互作用将不可避免地导致基岩的损坏。岩石破碎机制是刀岩相互作用的内在和基本机制的基础,也是提高TBM掘进效率的基础。因此,对圆盘刀具的岩石破碎机理有很高的理解要求。
圆盘刀具在岩石上的切削过程通常分为两个连续阶段,即压痕和滚动切削,实验室压痕试验和切削试验。在压痕阶段,刀具逐渐侵入岩石,直到达到预先设计的穿透深度。在这个过程中,裂纹在刀具-岩石接触区域下方开始,然后进一步深入地扩展。在底部切割器岩石接触面下方确定了四个独立的区域,即致密岩心、破碎区、裂缝区和弹性区。在随后的滚动切割阶段,刀具向前滚动,沿着切割轨迹产生裂纹和岩屑。岩屑可以是各种形状和大小,从而在开挖面上形成粗糙和不均匀的凹槽。刀具-岩石接触应力呈不规则分布,在切削过程中产生的刀具-岩石相互作用力波动,使刀具-岩石的相互作用难以理解。现有的理论推导通常会简化刀具-岩石相互作用应力,使其在切削方向上遵循规则分布,例如线性分布和垂直于切削方向的横截面上的赫兹分布。
切削力和磨损条件是切削试验的主要主题。然而,在实验室测试中很难识别切割过程中的岩石破碎和碎裂,因为只能观察到岩屑形成和宏观裂纹。一些研究人员尝试使用特殊技术(例如声发射)来捕捉岩石破裂事件。表面粗糙度的分析也让我们得以一窥刀具的性能和断裂机制。数值模拟是研究岩石破碎起始和发展的一种替代方法。特别是,离散单元法(DEM)将工程材料模拟为通过不同机制相互作用的颗粒组件,已被广泛用于模拟岩石切削过程。例如,2D DEM模拟。因此,在本文利用颗粒离散元PFC编程声发射矩张量代码对刀盘破岩过程进行模拟研究。
2. 建模方法
AE模拟算法在PFC(particle Flow Code)中的平行粘结模型(BPM)中实现,PFC是Itasca开发的显式离散元方法(DEM)的一个分支。这里,假设粒子是刚性的(不可变形的),并通过模拟粒子之间相互作用行为的接触模型结合。假设每一个粘结断裂都是一个微裂纹,并且每个微裂纹都会在测试期间导致AE活动。通过在测试期间监测所有粘结断裂,可以收集AE信息,并计算矩张量(MT),以分析断裂类型和破坏机制。
2.1. 平行粘结模型
平行粘结模型(BPM)作为一种离散元方法,最初由Cundall引入,并由Cundal和Strack开发。Potyondy等人详细描述了BPM的原理。该模型模拟了由二维或三维粘结的非均匀尺寸圆形或球形颗粒表示的固体材料的运动和相互作用。模拟材料的特性通常由颗粒和粘结键的刚度和强度微参数决定。商业软件PFC中提供了两种类型的BPM,即接触粘结模型和平行粘结模型。接触粘结作用于接触点,只能传递法向力和剪切力。平行粘结作用于两个颗粒之间的横截面,可以传递力和力矩,这是岩石或类岩石材料的更现实的粘结模型。
2.2. AE模拟和矩张量分解
当粘结键断裂时,源粒子将移动,相邻触点将发生一些变形。因此,由于裂纹的形成,周围接触处的力将发生变化。矩张量的分量可以通过将接触点处的力变化乘以接触点到裂纹位置的距离来计算。值得注意的是,AE事件可以由多个微裂纹组成。在空间和时间上紧密发生的微裂纹被视为一个AE事件,事件质心被假设为事件的几何中心(图1(a))。力矩张量可以通过在源边界周围积分来计算,对于离散元方法,积分由以下公式计算:

其中ΔFi是接触力变化的第i个分量,Rj是接触点和事件形心之间的距离。由于假设力矩张量是对称的,因此力矩张量的非对角分量将被假设为相等,并且将通过等式(1)计算的两个值进行平均来计算。此外,在AE事件持续期间的每个时间步计算矩张量,为每个AE事件存储的单个矩张量是在最大标量力矩的时间步计算的结果。
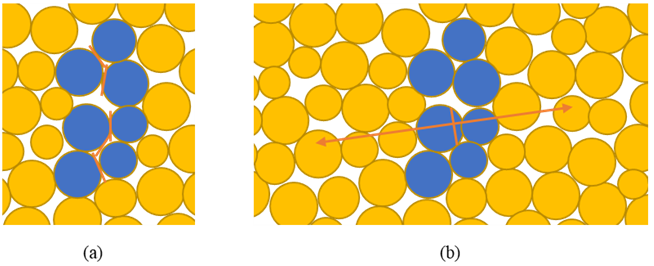
图1 示例AE事件及矩张量示意图
矩张量可以被认为是源的等效体力,矩张量表示将矩张量矩阵的主值描述为两组向量,其方向和长度分别表示方向和大小(图1(b))。
将公式(1)计算得到的矩张量分解为球张量与偏张量,则声发射破裂类型可根据球张量占比Piso进行判定

2.3. 模型描述
建立的圆盘刀具破岩的数值模型长度是1 m,高度为0.5 m,在该模型中总共产生12087个球形颗粒。同时,墙命令用于在左侧、右侧和底部建立刚性边界。假设圆盘刀具是刚性材料,并且在模型计算过程中刀具不会磨损。类似地,圆盘刀具是由PFC2D中的墙命令生成的。为了便于建模,现场CCS型圆盘刀具被简化为六边形,如图2所示。
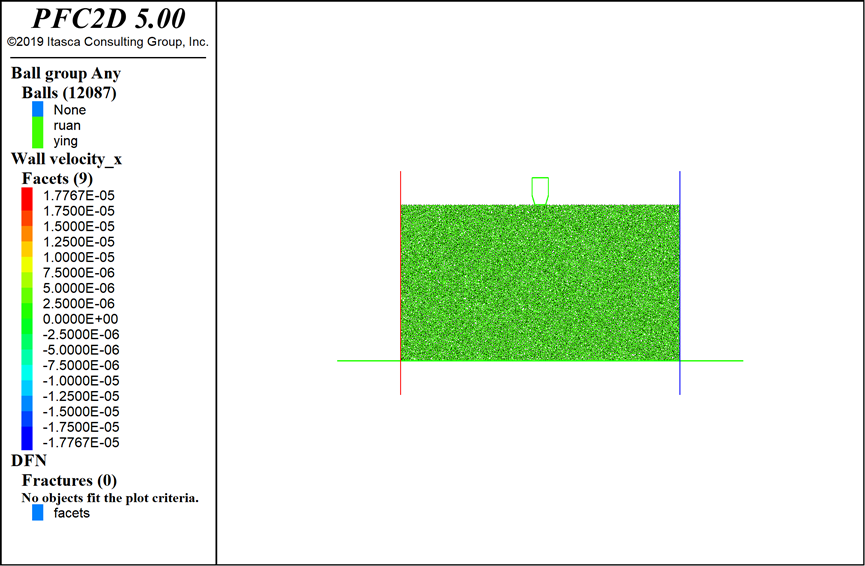
图2 数值模型
3. 模拟结果分析
3.1. 震级分布
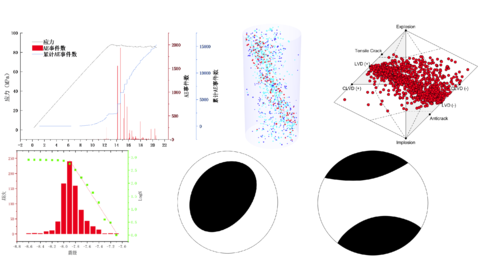
通过PFC声发射矩张量代码可以直接反演出破岩产生的声发射事件分布及震级,其结果如图3所示。
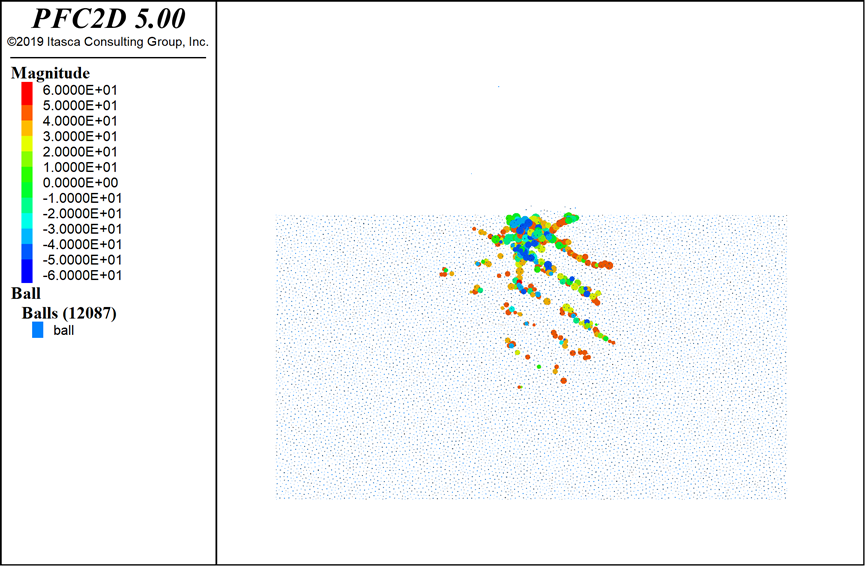
图3 震级分布
3.2. 不同类型裂纹空间分布图
应用矩张量分析程序对试样在刀盘作用下的声发射信号进行分析,图4显示了声发射空间分布,利用模拟结果导出文件可将破坏模式分为拉伸、剪切和混合。图4中蓝色圆圈表示拉伸型裂纹,红色圆圈表示剪切型裂纹,绿色圆圈表示混合型裂纹。
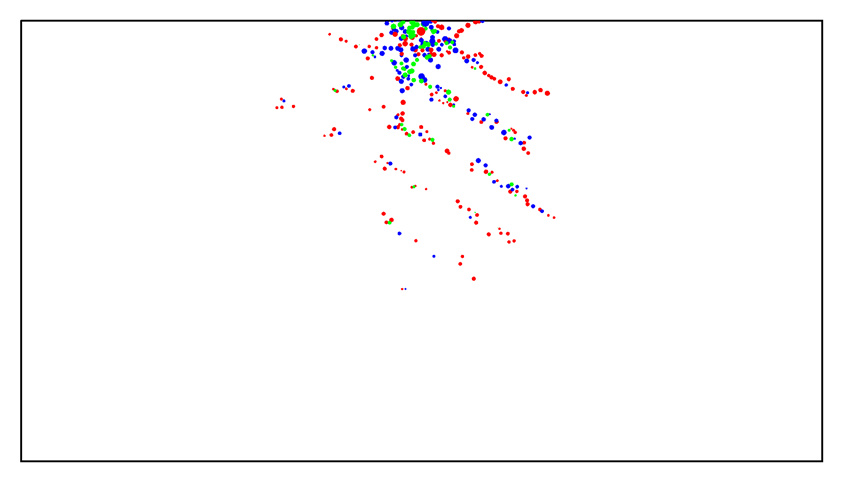
图4 不同类型裂纹空间分布图
3.3. 声发射特征分析
在模拟过程中,通过矩张量文件中aenum记录了AE事件,进而可以做出应力应变、AE事件数和累计AE事件数之间的关系,如图5所示。
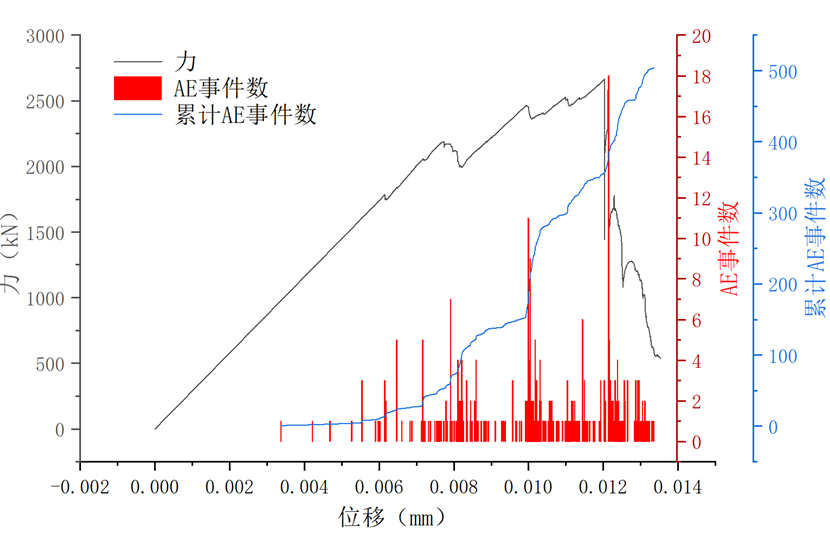
图5 AE事件和AE累积事件的演变过程
内容简介:附件包含颗粒离散元PFC的圆盘刀具破岩过程声发射矩张量模拟代码