数值计算 | 如何利用高斯散度定理计算多面体几何属性
0
写在前面
1
高斯定理
2
计算体积
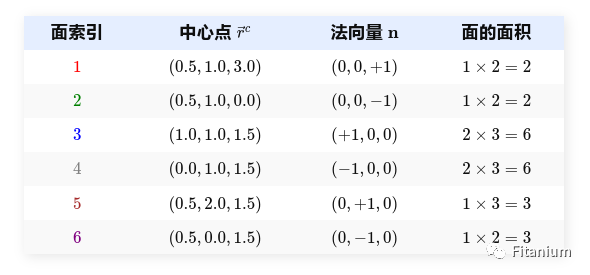
3
计算质心
注:上面推导使用了公式
Improved Formulation for Geometric Properties of Arbitrary Polyhedra.
The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab.
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-04
最近编辑:1年前
还没有评论
相关推荐
最新文章




