基于颗粒离散元PFC的三维巴西劈裂过程的声发射矩张量模拟
本文摘要(由AI生成):
本文研究了岩石或类岩石材料中颗粒间的行粘结作用,并通过离散元方法模拟了岩石在加载过程中的破坏模式。利用声发射(AE)技术,对模拟过程中的AE信号进行了矩张量分析,以揭示岩石破裂的类型和复杂性。模拟结果显示了破坏模式、力-位移曲线和震级分布,并通过矩张量分解将破裂类型分为拉伸、剪切和混合。后处理得到的AE事件空间分布图揭示了不同类型AE事件的空间分布。此外,通过AE b值评估了裂缝网络的复杂性,较大的b值表示更复杂的裂缝网络。菱形图用于直观显示矩张量分解结果,并确定了AE事件的走向角、倾角和滑移角,进而绘制了相应的玫瑰图。
基于颗粒离散元PFC的三维巴西劈裂过程的声发射矩张量模拟
1、引言
岩石的抗拉强度远低于抗压强度,因此在地下工程、深部采矿和储能工程中,拉伸破坏经常发生。岩石拉伸破坏是围岩失稳的主要形式之一。因此,对于各种岩石工程的设计和稳定性分析来说,岩石的抗拉强度是一个重要的控制参数。准确获取岩石抗拉强度对保证工程建设和防灾安全具有重要意义。
抗拉强度的测试有两种方法,即直接测量和间接测量。虽然直接测量方法具有较高的精度,但很难实现,例如很难确保轴向载荷完全沿着试样的轴线,而且试样的断裂不一定在中间,这些困难将严重影响试验结果,因此通常采用间接测量。巴西分裂法是间接测量中使用最广泛的方法。因此,利用离散元软件PFC分析了巴西劈裂过程中声发射矩张量特征。
2. 建模方法
AE模拟算法在PFC(particle Flow Code)中的平行粘结模型(BPM)中实现,PFC是Itasca开发的显式离散元方法(DEM)的一个分支。这里,假设粒子是刚性的(不可变形的),并通过模拟粒子之间相互作用行为的接触模型结合。假设每一个粘结断裂都是一个微裂纹,并且每个微裂纹都会在测试期间导致AE活动。通过在测试期间监测所有粘结断裂,可以收集AE信息,并计算力矩张量(MT),以分析断裂类型和破坏机制。
2.1. 平行粘结模型
平行粘结模型(BPM)作为一种离散元方法,最初由Cundall引入,并由Cundal和Strack开发。Potyondy等人详细描述了BPM的原理。该模型模拟了由二维或三维粘结的非均匀尺寸圆形或球形颗粒表示的固体材料的运动和相互作用。模拟材料的特性通常由颗粒和粘结键的刚度和强度微参数决定。商业软件PFC中提供了两种类型的BPM,即接触粘结模型和平行粘结模型。接触粘结作用于接触点,只能传递法向力和剪切力。平行粘结作用于两个颗粒之间的横截面,可以传递力和力矩,这是岩石或类岩石材料的更现实的粘结模型。
2.2. AE模拟和矩张量分解
当粘结键断裂时,源极粒子将移动,相邻触点将发生一些变形。因此,由于裂纹的形成,周围接触处的力将发生变化。力矩张量的分量可以通过将接触点处的力变化乘以接触点到裂纹位置的距离来计算。值得注意的是,AE事件可以由多个微裂纹组成。在空间和时间上紧密发生的微裂纹被视为一个AE事件,事件质心被假设为事件的几何中心(图1(a))。力矩张量可以通过在源边界周围积分来计算,对于离散元方法,积分由以下公式计算:

其中ΔFi是接触力变化的第i个分量,Rj是接触点和事件形心之间的距离。由于假设力矩张量是对称的,因此力矩张量的非对角分量将被假设为相等,并且将通过等式(1)计算的两个值进行平均来计算。此外,在AE事件持续期间的每个时间步计算力矩张量,为每个AE事件存储的单个力矩张量是在最大标量力矩的时间步计算的结果。
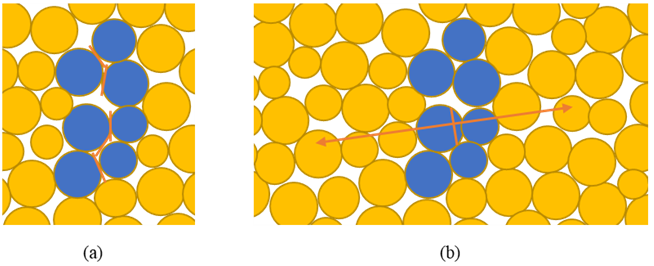
图1 示例AE事件及矩张量示意图
矩张量可以被认为是源的等效体力,矩张量表示将矩张量矩阵的主值描述为两组向量,其方向和长度分别表示方向和大小(图1(b))。
将公式(1)计算得到的矩张量分解为球张量与偏张量,则声发射破裂类型可根据球张量占比Piso进行判定

2.3. 模型描述
数值试样的尺寸与实验试样的尺寸相同(如图2所示),高度为25 mm,直径为50 mm。考虑到计算时间,颗粒尺寸遵循1 mm至1.66 mm的均匀分布,样品中总共产生4670个颗粒。

图2 数值模型
3. 结果分析
模拟直接得出的破坏模式、力-位移曲线和震级分别如图3所示。

(a) 破坏模式
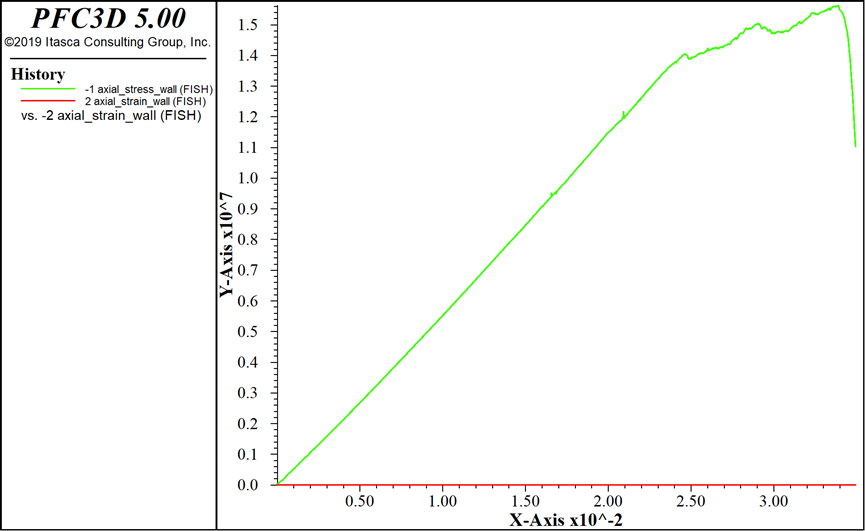
(b) 力-位移曲线
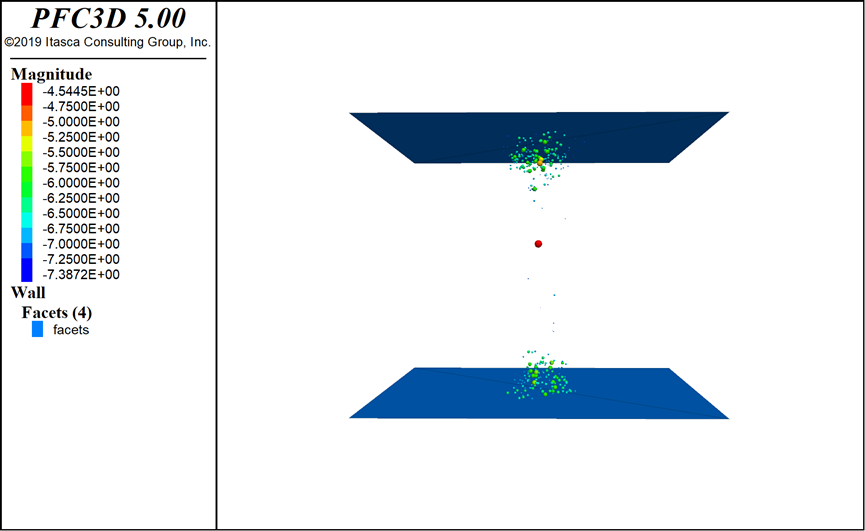
(c) 震级分布
图3 模拟直接得到的结果
模拟得到的dat文件如图4所示。
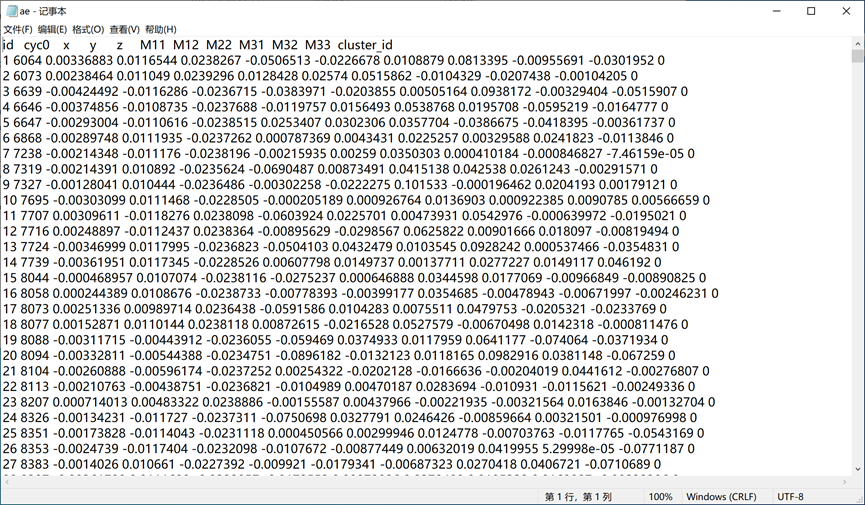
(a) AE
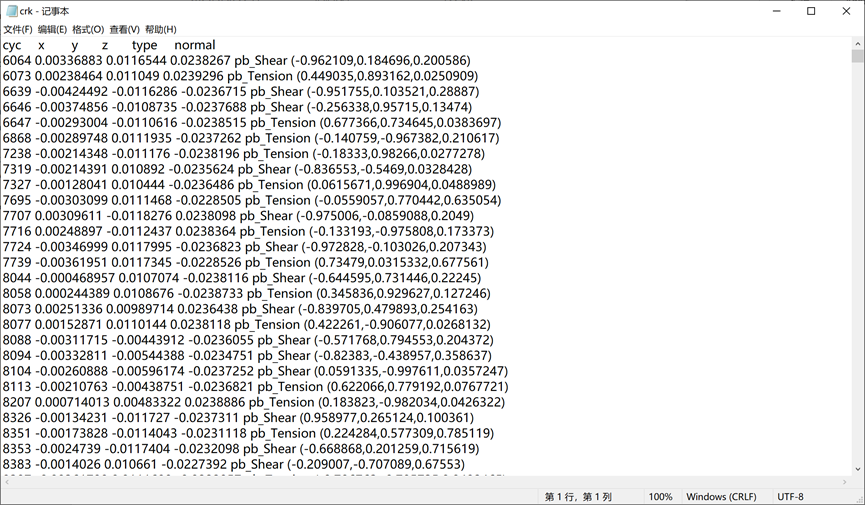
(b)裂纹文件
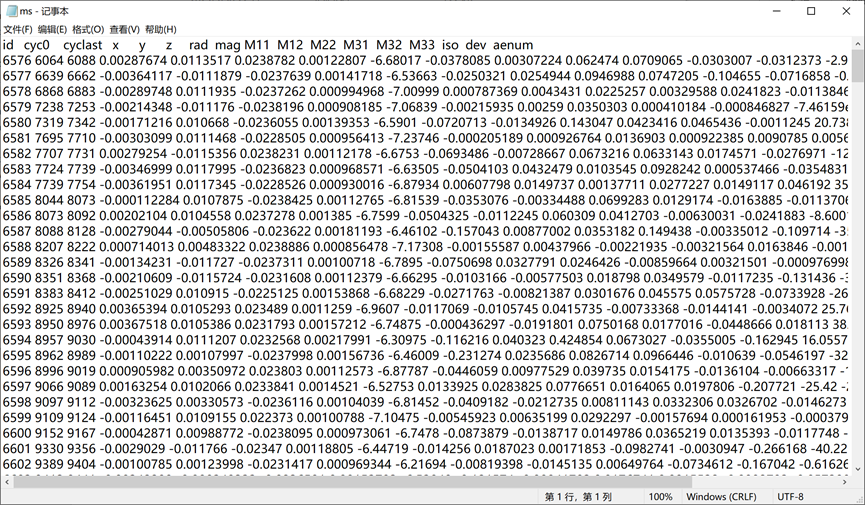
(c)矩张量文件
图5 模拟得到的dat文件
3. 后处理得到结果
应用矩张量分析程序对试样在加载作用下的声发射信号进行分析,图6显示了声发射空间分布,利用图5(c)中ios和公式(2)可将破坏模式分为拉伸、剪切和混合。图6中青色球体表示剪切事件,蓝色球体表示张拉事件,红色球体表示混合事件,球体大小表示能力和震级的相对大小。此图为去掉仅有1条裂纹的声发射事件的定位图。
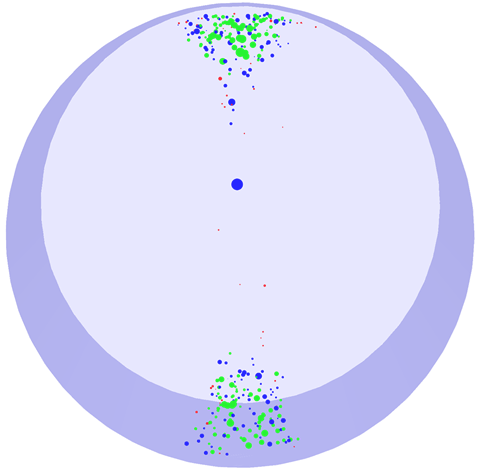
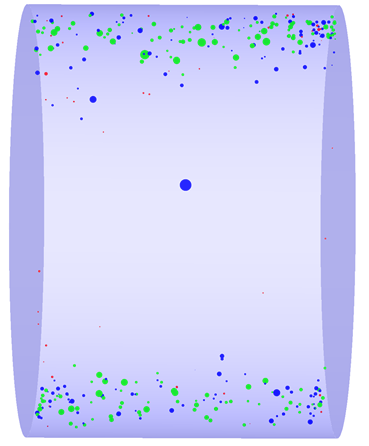
图6 不同类型AE事件空间分布图
在模拟过程中,通过矩张量文件中aenum记录了AE事件,进而可以做出应力应变、AE事件数和累计AE事件数之间的关系,如图7所示。
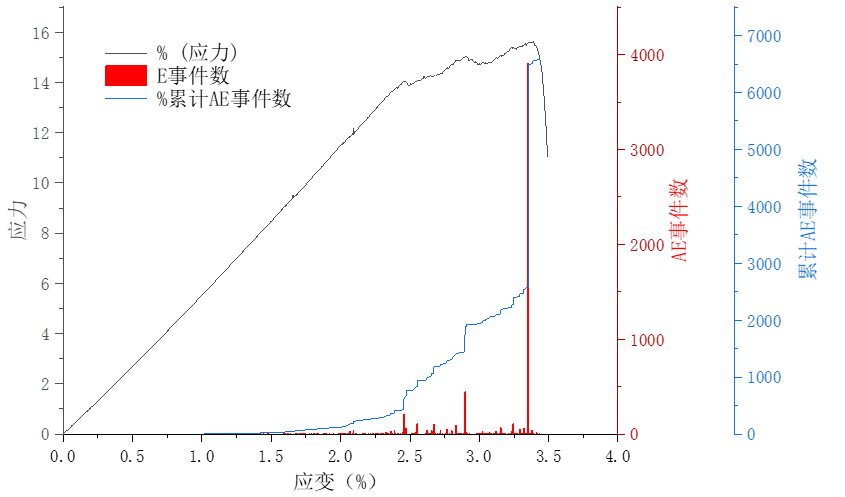
图7 AE事件和AE累积事件的演变过程
4. 通过AE b值评估裂缝网络的复杂性
断裂系统的产生伴随着现场的微震或实验室的AE,这有助于描述断裂分布。同时,我们注意到,Gutenberg和Richter提出的b值不仅可以用于描述AE震级的分形特征,还可以用于描述声发射源的空间分形特征。较大的b值意味着更复杂的裂缝网络,而较小的b值则意味着更简单的裂缝网络。描述地震震级和频率之间关系的古腾堡和里希特公式如下:

其中M为地震震级;N是震级大于M的地震的累积次数;a和b是两个统计常数。根据矩张量文件中的mag列数据可以得出下图,进而求出b值。
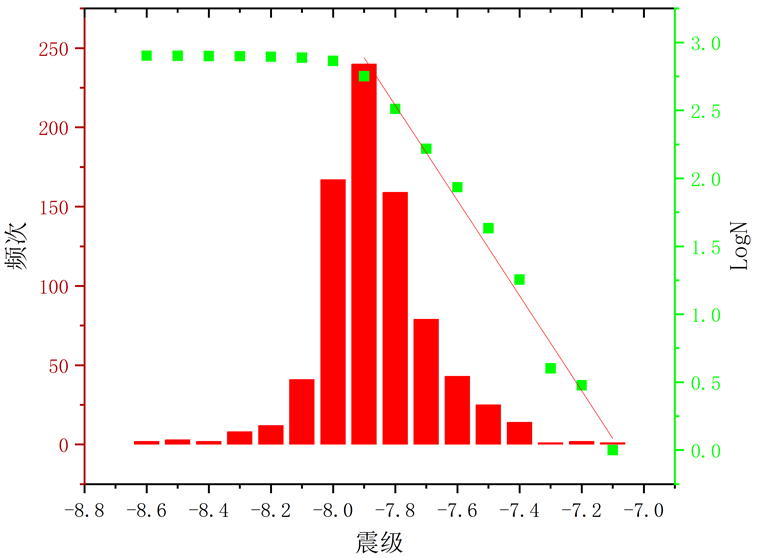
图8 AE事件数量和AE震级的关系(直方图显示频率-震级分布,散点显示大于某个震级的AE事件数量)。
5. 菱形图
矩张量分解可以使用菱形图来显示和容易地解释。该图显示了源在CLVD–ISO坐标系中的位置,其中双力偶分量由颜色强度表示。具有纯剪切断层或主要剪切断层的震源位于坐标原点或附近。爆炸和内爆分别位于钻石的顶部和底部顶点。纯拉伸和压缩裂纹绘制在钻石的边缘。沿着CLVD轴的点对应于非平面断层上的断层,菱形图的第一和第三象限中的点对应于剪切拉伸源。
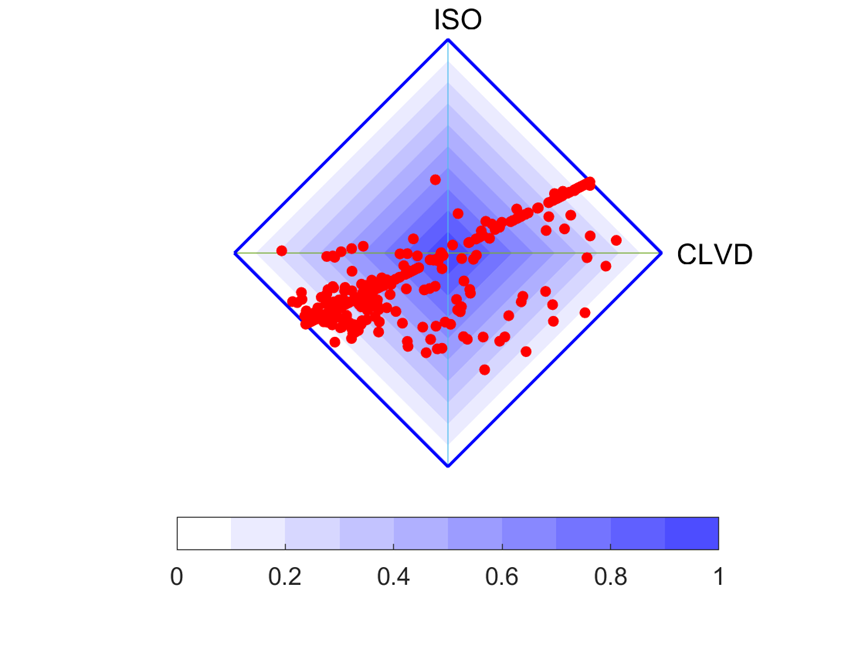
图9 菱形图
6. AE事件走向角(strike)、倾角(dip)和滑移角(rake)确定
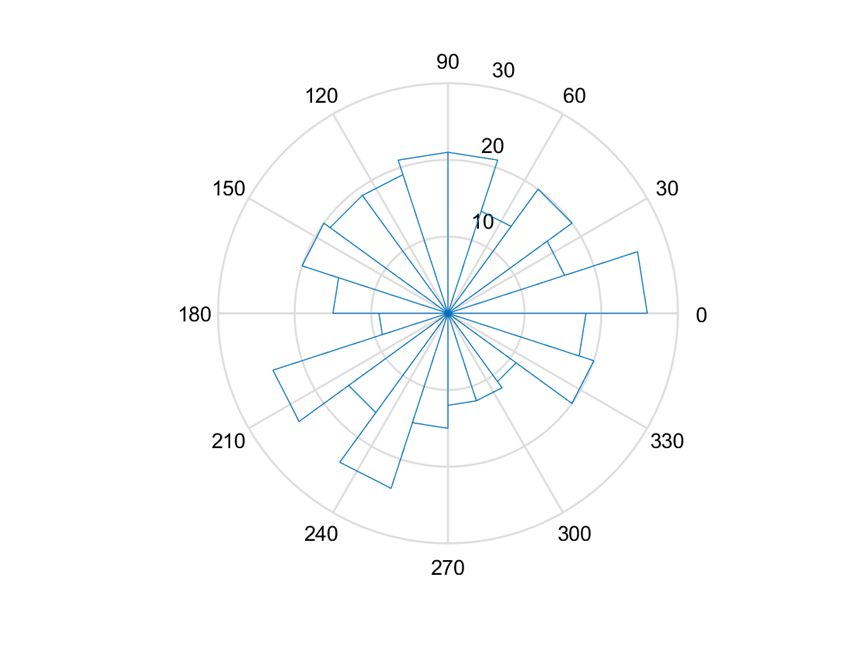
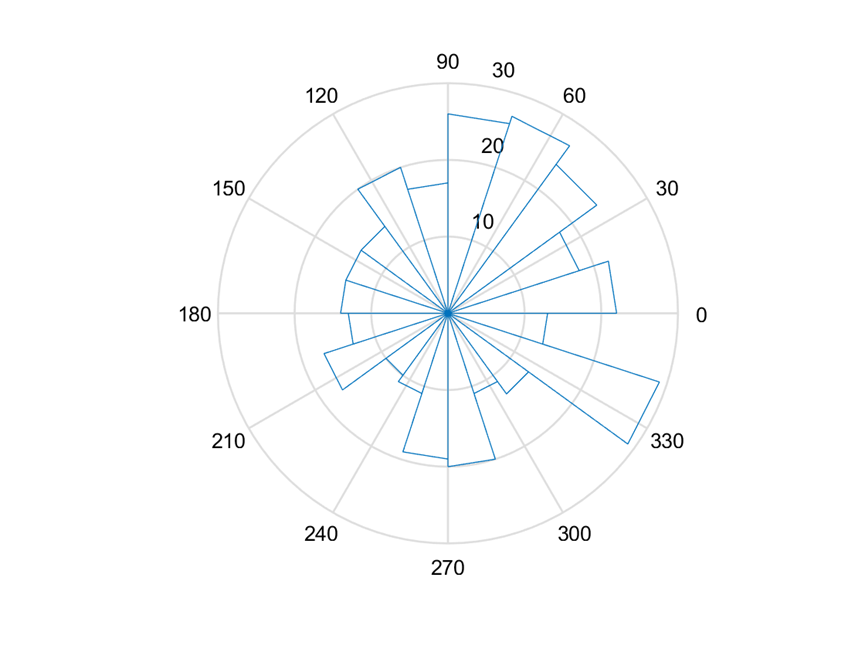
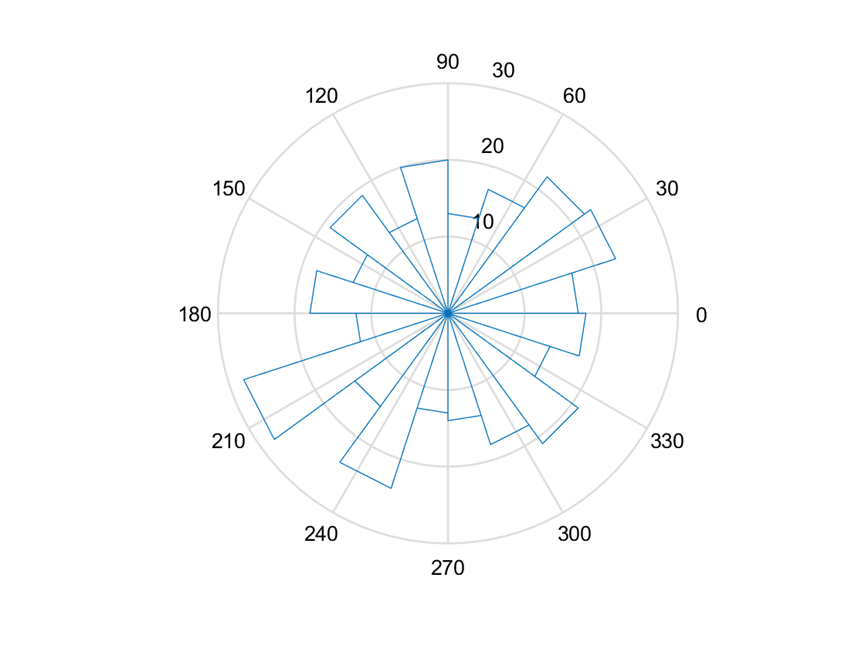
利用MATLAB可得出图10所示数据。其中包含声发射事件的走向角(strike)、倾角(dip)和滑移角(rake)。利用这些信息可以做出声发射事件的走向角(strike)、倾角(dip)和滑移角(rake)的玫瑰图。
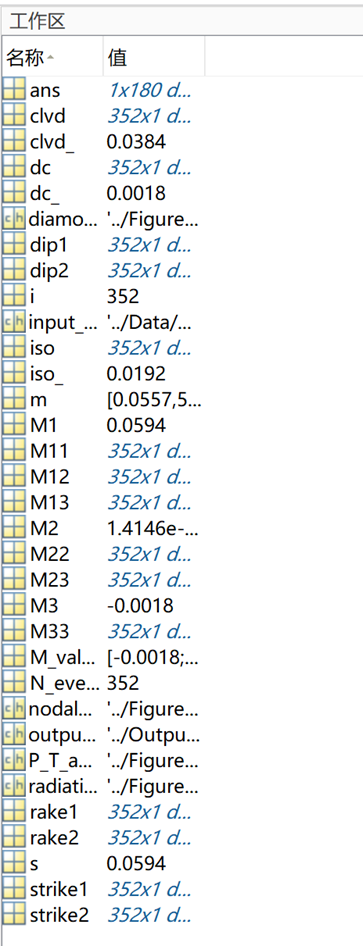
图10 MATLAB代码导出数据
(a)走向角(strike)
(b)倾角(dip)
(c) 滑移角(rake)
图 11 角度玫瑰图
内容简介:包含三维巴西劈裂PFC声发射矩张量模拟代码和MATLAB菱形图和角度反演代码