冯卡门也犯错?大桥振动和卡门涡街到底什么关系?
冯卡门也犯错?大桥振动和卡门涡街到底什么关系?
张伟伟 李新涛 豆子皓 高传强
西北工业大学
摘 要:首先介绍了卡门涡街、涡激振动和颤振的概念。在此基础上,讲述历史上塔科马大桥风毁事件的研究争论,并再次澄清塔科马大桥风毁的原因是颤振而不是涡激共振,故与卡门涡街无关。最后,对虎门大桥振动问题,针对风工程领域中涡激振动问题的性质进行了讨论,指出限幅涡振问题,并伴随的锁频现象,本质上仍是结构自激振动问题,卡门涡街起到的是诱发而不是直接的推动作用。
作者简介:张伟伟

目前主要从事三个方向的研究:(1)气动弹性力学(2)智能流体力学(3)理论与计算流体力学。主持国家自然基金5项,863项目3项,重大专项2项,其他省部级项目10余项。完成航空、航天、兵器等单位型号及预研项目20余项,解决了多个关键技术难题。
1979年8月,工学博士,西北工业大学教授。现任西北工业大学航空学院副院长,流体力学智能化研究所所长。获得省部级科技奖5项,授权发明专利7项,撰写著作1本。在国内外刊物和学术会议发表论文100余篇。现任中国空气动力学会理事,陕西省力学学会理事,Aerospace Science and Technology期刊副编辑,航空学报,空气动力学报,实验流体力学,气体物理,航空工程进展等期刊的青年编委。
近日,虎门大桥的振动引起了学术界和网友们的广泛关注和讨论。很多土木工程领域的学者第一时间指出这应该是大跨度桥梁较常见的涡振,对桥梁的破坏并不剧烈。然而不少自媒体进一步引申出1940年塔科马大桥的倒塌事件来说明涡振的剧烈程度和破坏性。再简单搜索共振,卡门涡街和塔科马大桥,都能在词条中看到“卡门涡街或共振是塔科马大桥倒塌的原因”等描述。甚至在初高中的课堂上,塔科马大桥风毁事件都作为共振与卡门涡街的典型案例进行讲述。这引发了笔者撰写本文的驱动力,有必要从气动弹性力学者的角度解释几个不同的气动弹性力学概念。
卡门涡街,涡激振动和颤振
首先简单介绍一下这几个名词的概念:
卡门涡街:在一定条件下的定常来流绕过钝型物体时,物体两侧会周期性地交替脱落出旋转方向相反、并排列成有规则的双列线涡,如图1所示。由于冯∙卡门(美国航天之父,钱学森的导师)最先研究该现象,故被命名为卡门涡街。



图1 从空中俯瞰云团流过岛屿形成的与数值模拟的卡门涡街



图2 圆柱的涡激振动模型与动画



(a)无人机发生颤振解体(b)滑翔机发生非线性颤振
图3 颤振现象
Tacoma大桥风毁事件始末

图4 Tacoma大桥扭转振动并坍塌
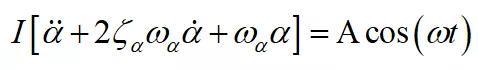 (1)
(1)
图5 教科书中将卡门涡街作为Tacoma扭转振动的解释
 (2)
(2)

图6 Dowell教授专著中对Scanlan教授颤振解释的肯定
虎门大桥的振动
1)很多问题中的频率锁定范围会远远偏离共振的频率比范畴(0.85-1.15),频率比甚至超过1:2;
2)很多时候的最大振幅并不是在共振点处取得;
3)非线性共振的机制是什么?什么机制促使结构响应频率不跟随外激励力频率?


图7 Re=60圆柱涡致振动现象示意图:
(a)振动幅值;(b)振动频率

图8 线性稳定性分析得到的耦合系统根轨迹

图9 Re=40的定常绕流图

图10 Re=40,沉浮刚度释放后的涡激振动动画

图11 亚临界雷诺数(Re=33)下耦合系统的根轨迹

图12 亚临界雷诺数(Re=33)下的涡致振动振幅和频率随风速的变化
颤振、涡振以及其它流致振动问题
结 论
结束语
参考文献
[1]Von Kármán, Theodore. Aerodynamics : Selected Topics in the Light of Their Historical Development[M]. Cornell Univ. Press, 1954.
[2]Larsen, Allan. Aerodynamics of the Tacoma Narrows Bridge - 60 Years Later[J]. Structural Engineering International, 2000, 10(4):243-248.
[3]Beckett. D. Great Buildings of the World-BRIDGES[M]. Paul Hamlyn. London. 1969.
[4]Scanlan R, Tomko JJ. Airfoil and bridge deck flutter derivatives[j]. J. Eng. Mech. 1997, 97:1717-1737
[5]Billah KY, Scanlan RH. Resonance, Tacoma Narrows Bridge failure, and undergraduate physics textbooks[J]. American Journal of Physics, 1991, 59(2):118-124.
[6]Dowell E H, Robert C,Et al. A Modern Course in Aeroelasticity[M]. Kluwer Academic Publisher, 2005, P306&P330. (杨智春等译,2013,航空工业出版社)
[7]陈政清. 桥梁风工程(高等学校教材)[M]. 人民交通出版社, 2005.
[8]Zhang WW, Li XT, Ye ZY, eta. Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers[J].Journal of Fluid Mechanics, 2015, 783: 72-102.
[9]Gao C, Zhang W, Li X, et al. Mechanism of frequency lock-in in transonic buffeting flow[J]. Journal of Fluid Mechanics, 2017, 818: 528-561.
[10]Kou J, Zhang W, Liu Y, et al. The lowest Reynolds number of vortex-induced vibrations[J]. Physics of Fluids, 2017, 29(4): 041701
[11]Li XT, Lyu Z, Kou JQ, etc. Mode competition in galloping of a square cylinder at low Reynolds number[J].Journal of Fluid Mechanics, 2019, 867: 516-555.
[12]Gao C, Zhang W. Transonic aeroelasticity: A new perspective from the fluid mode[J]. Progress in Aerospace Sciences, 2020,113, 100596.
声明:原创文章,首发气动弹性力学与流动控制公 众号,本文已经授权,如需转载请联系作者。




