弹性力学中的平面问题
序言

任何一个弹性体都是空间三维的,其受力也是空间力系,因此,严格讲所有的弹性力学问题都是空间问题。但如果考察的结构具有某种特殊形状、以及其受力具有某种特殊形式,就可以忽略一些方向上的影响,把空间三维问题简化为平面问题,从而在满足工程精度需要的前提下,降低力学问题求解的工作量。
1
弹性力学中的平面问题分类

在弹性力学问题求解中,有三类典型的平面问题:
1)平面应力
等厚度薄板,外力平行于板面且不随厚度变化。这种情况下,沿板厚方向的应力可忽略(假设为零),平行于板平面方向的应力分量不为零,因此叫做平面应力问题。

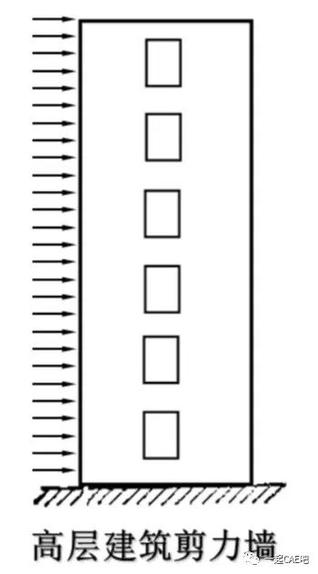
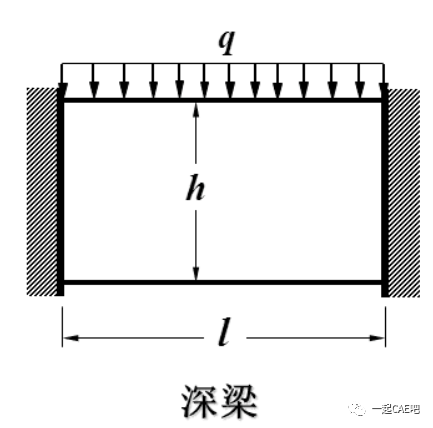
平面应力问题三要素:
平面
薄板(厚度远小于其他方向尺寸)
外力沿厚度方向分量为零且大小不随板厚变化。
2)平面应变
等截面长柱体或圆筒等结构,外力平行于截面且不沿长度变化。这种情况下,沿长度方向的应变可忽略(假设为零),而平行于截面的方向应变分量不为零,因此叫做平面应变问题。


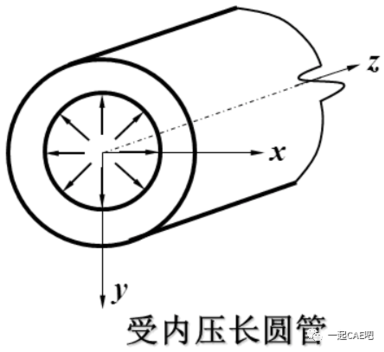
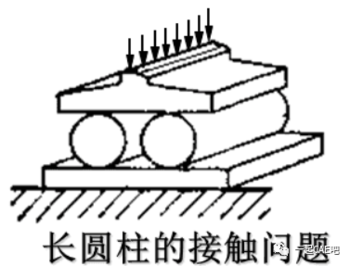

平面应变问题三要素:
等截面
长度尺寸远大于其他方向尺寸
外力平行于截面且不沿长度变化
3)轴对称
在工程问题中经常会遇到一些实际问题,如旋转机械中的盘、轴、承力环及支撑圈等,它们都有一个对称轴,而整个物体是通过轴的一个平面上某个图形绕此轴旋转而成的回转体,称之为轴对称体。如果轴对称体的载荷是轴对称的,其约束也是轴对称的,则在载荷作用下产生的位移、应变和应力必然是轴对称的,这种结构的应力分析问题称轴对称问题。
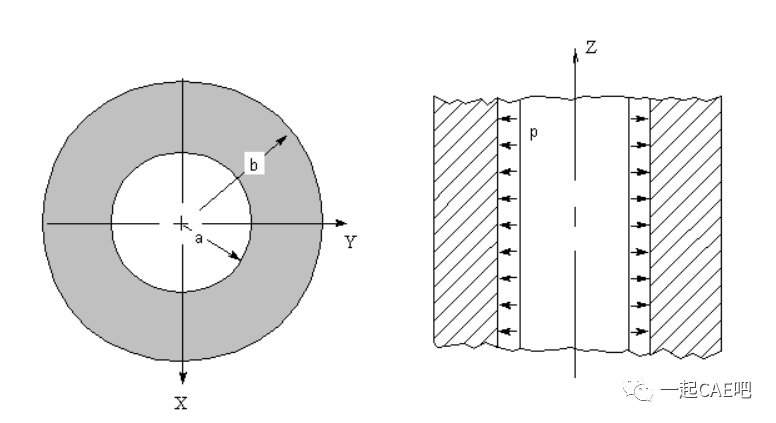
轴对称问题三要素:结构、载荷和约束均为轴对称。
2
弹性力学的三大方程及平面简化

2.1
三维问题的弹性力学方程

弹性力学是固体力学的一个分支,其研究弹性体由于受到外力或温度改变等原而发生的位移、形变和应力。
弹性力学的研究方法是,在弹性体内部(一般取一个如下图所示的微元体作为研究对象)按照静力学、几何学和物理学的条件建立平衡微分方程、几何方程和物理方程。在边界上根据受力情况或约束条件建立应力边界条件或位移边界条件,边界条件结合以上方程即可以进行弹性力学问题的求解。

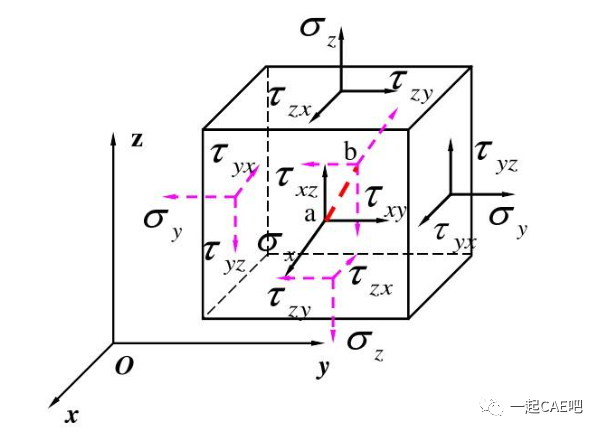
1)平衡微分方程-表征内力与外力之间的平衡关系
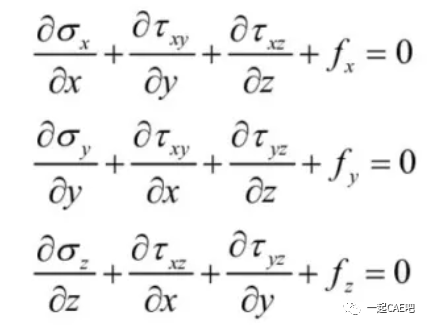
2)几何方程-表征应变分量与位移分量之间的关系
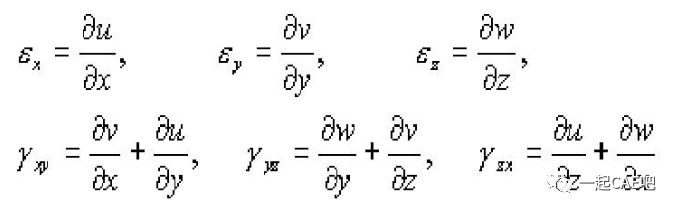
3)物理方程-表征应力分量与应变分量之间的关系
物理方程又叫本构方程,是有广义胡克定律推导而来。

以上三大类方程共15个方程式,包含15个变量(即6个应力分量、6个应变分量、3个位移分量)。
2.2
平面问题弹性力学方程简化

空间三维问题的弹性力学求解涉及到偏微分方程,一般来说是比较困难的,而如上所述,一些特殊的结构可以简化为平面问题,从而降低求解难度。
以物理方程为例,平面问题的物理方程简化如下。
1)平面应力
平面应力状态适合于薄平板结构,受平行于平板方向的外力作用。假设Z轴方向(薄板厚度方向)无应力。即Z轴方向应力为0。
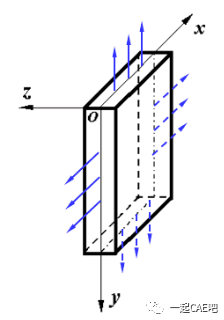
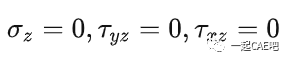
此时薄平板只受到X、Y轴方向的应力作用。将上述应力条件代入到广义胡克定律中,得出平面应力状态下的物理方程:
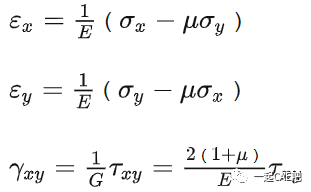
2)平面应变
平面应变的变形只发生在平面内,此时受垂直于长度方向的均布力,假设长度方向无变形,定义长度方向为Z,即,Z轴方向应变为0。
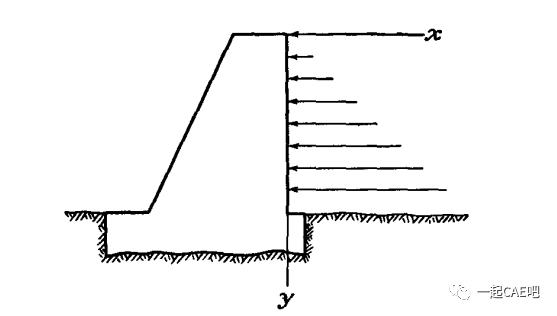

此时变形只在 X、Y 方向发生。将上述应力条件代入到广义胡克定律中,有:
![]()
将上述变量等式代入物理方程,得到平面应变的物理方程如下:
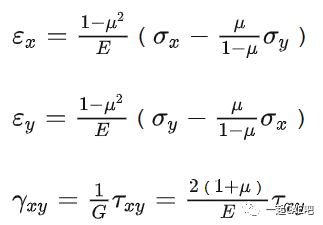
3)平面应力与平面应变之间的转换
以上推导可以看出,平面应力和平面应变的物理方程形式上一样,只是其系数不同,实际上,他们之间可以通过一定的关系进行转换,如下图所示。
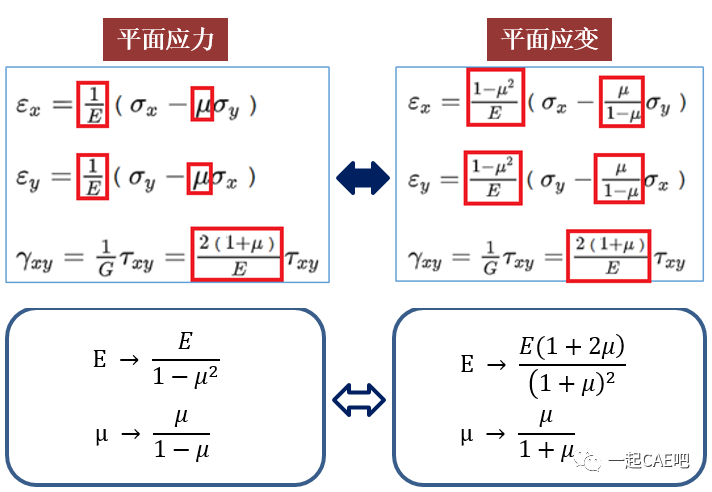
4)轴对称问题简化
在轴对称问题中,通常采用圆柱坐标(r,θ,Z),对称轴为Z轴,半径方向为r轴,其正方向如图所示,以Z轴为正向的右螺旋转动方向表示θ的正向。
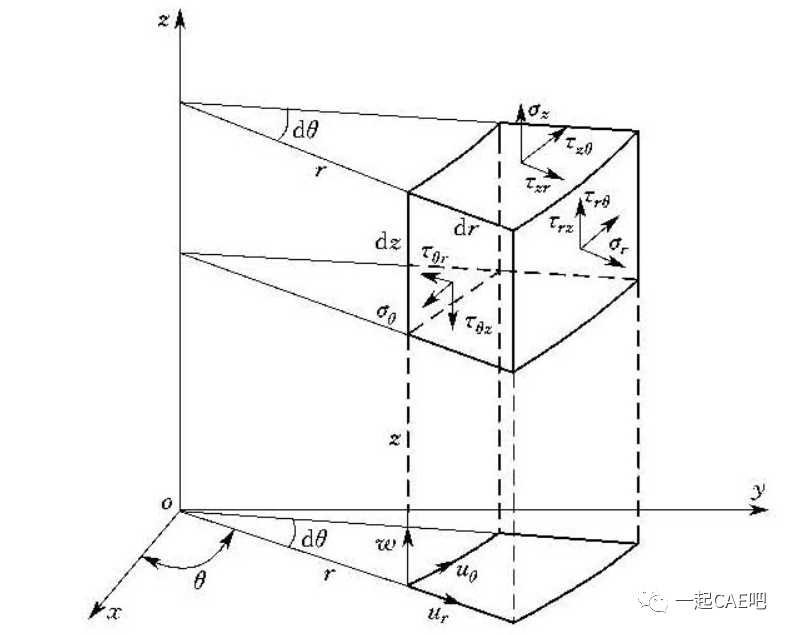
空间轴对称问题虽属三维问题,但由于几何形状的轴对称性,在轴对称载荷作用下,所产生的位移、应变和应力与θ无关,只是r和Z的函数,任一点的位移只有两个方向的分量,即沿r方向的径向位移和沿Z方向的轴向位移。由于轴对称,θ方向的位移v等于0,因此轴对称问题是准二维问题,它可以按平面问题处理,但注意其与平面问题不完全相同。

END





