SolidWorks Simulation 有限元分析实例练习（3）：局部网格控制

在实际的问题中，网格很很少是完全均匀的。仅因为局部应力集中的因素，而在一个模型中均匀的降低网格的大小是非常不明智的，这将会导致计算量的增加，而最终的结果可能没有多大的差别。

这就需要我们对网格进行控制，即在需要分析的位置进行小单元的划分，在无应力集中的位置用较大的网格划分。

下面我们通过一个L形支架为例，支架的拐角处忧郁哥圆角，圆角半径非常小，可以将其忽略。我们将对带有圆角和不带圆角的模型进行分析求解，讨论它们的区别。本文先在忽略圆角的情况下通过局部网格控制策略对模型进行分析。

点击阅读原文下载模型

方法：

1.打开模型，模型有两种配置，一种带有圆角，另一种没有圆角。

2.设置Simulation选项。单击simulation菜单中单击【选项】，选择默认选项选项卡。在【单位系统】中，设置好单位；在【颜色图表】设置数字格式的科学，小数位数设置为6。

3.创建名为mesh 1的算例，类型选择【静应力分析】。

4.接下来进行模型的预处理。

1）设置材料。我们发现材料已经定义了，它是从SolidWorks传送过来的。

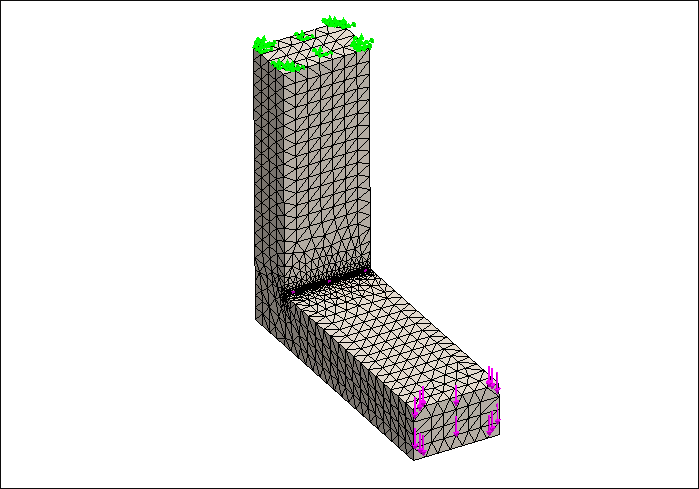
2）添加夹具。对支架上端面施加【固定几何体】约束。点击夹具鼠标右键选择“固定几何体”。

3)施加载荷。选择外部载荷，鼠标右键选择“力”。这里添加一个剪切力而不是法向力，选择【选定的方向】，按照下图进行设置。

5.划分网格。在特征树下选择网格，鼠标右击选择【生成网格】，在网格参数下选择【基于曲率的网格】，其他选项全部默认。

6.复 制算例mesh1，创建mesh2。

7.在mesh2中，选择特征树中的网格，鼠标右击选择【应用网格控制】，选择下面的箭头所指的边线，默认全部的设置。

使用建议的局部单元大小为2.4062mm，比率为1.5。比率是用来定义连续过渡单元层单元大小。

7.选择网格鼠标右击选择【生成网格】，在网格参数下选择【基于曲率的网格】，其他选项全部默认。

8.复 制mesh2，创建mesh3。

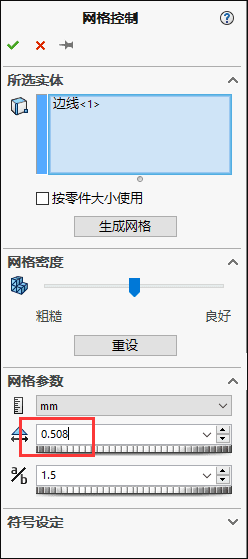
9.在特征树选择控制1，鼠标右击选择【编辑定义】，在单元大小框中输入0.508以进行局部细化，保持比率的默认值为1.5。

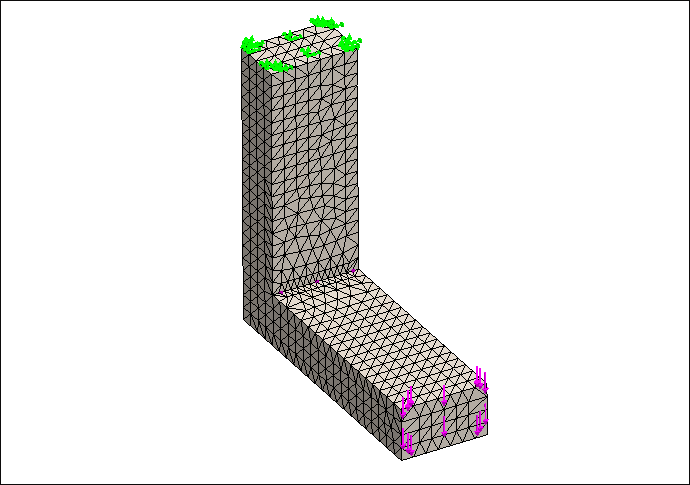
10.生成网格。在网格下选择【基于曲率的网格】，其他选项全部默认。下图依次是mesh1、mesh2和mesh3的网格划分结果，我们可以看到三个网格不同之处在于尖锐拐角边缘网格划分的精细度。

11.运行所有的算例。

12.如果我们在想显示图解同时显示网格，我们可以点击相应的图解鼠标右键选择“设定”。

将边界选项设置为网格，如下图所示。

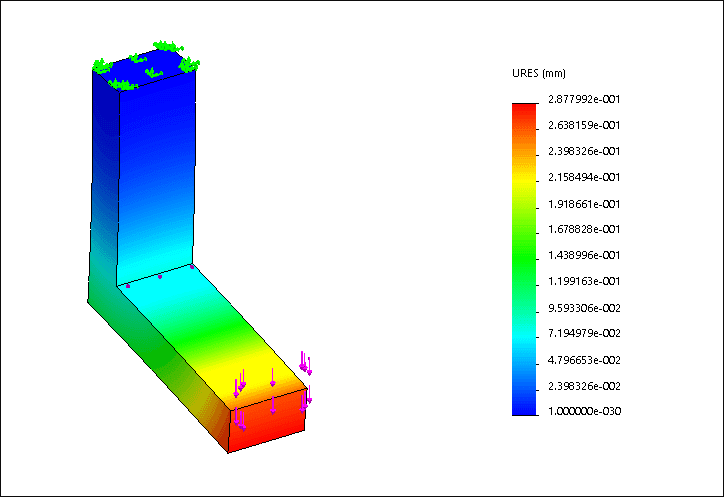
13.我们可以得到如下图所示的三个分析的von Mises应力值。

14.我们可以得到如下图所示的三个分析的合位移值。

15.结果分析。下表显示了三个分析的最大位移和最大von Mises应力值。

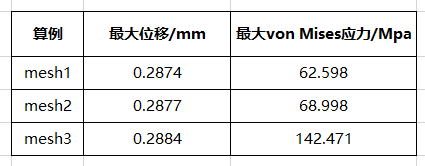
每次网格的精细化都会增加最大位移和最大von Mises应力值。位移的增加是比较小，趋向于一个有限值，基本可以认为位移结果是收敛的。

然而应力的情况却大不相同。随着网格的精细化，得到的应力值越来越大，是一个发散的数值。如果我们继续划分网格，将会得到各种大小的应力结果。

导致应力结果发散不是因为有限元模型本身的错误，而是有限元模型基于一个错误的数学模型。根据弹性理论，尖角处的应力是无穷大的。由于离散化误差，有限元模型并不会产生无穷大的应力结果。

如果我们的目的是确定最大应力值，那么忽略圆角的存在，导致模型含有一个尖锐的拐角是一个严重的错误。如果想了解圆角附近的应力情况，那么不管圆角的尺寸多么小，都应该在模型中将其包含进来。