SolidWorks Simulation 有限元分析实例练习(12):虎钳受力分析(2)
上一节我们通过225N的力施加在手柄上,现在我们在手柄上施加一个更大的力使得两个钳臂互相接触。

点击阅读原文下载模型
方法:
1.首先我们通过复 制的方法创建一个新的算例。

2.编辑载荷力的大小。
将力的大小设置为4000N。
为什么施加的力的大小为4000N呢?上一节虎钳在225N的力的作用下,手柄的末端移动了0.529mm,即手柄末端的距离减少了1.058mm。两个手柄最初的距离为15.24mm,基于线性分析的假设,即结构的响应与所加载的力成比例,可以计算出使两个钳臂接触在一起的力量为:3241N。这里我们选择4000N,这样才可以确保钳臂可以接触在一起。

3.定义接触对。因为外力远大于使两个钳臂接触在一起的力,所以需要指定一个局部接触条件来阻止它们之间的相互穿透。
无穿透的顶层装配体零件接触只能应用在初始相互接触的面上。
局部接触条件比零部件接触条用于更高的优先权。一般来说,顶层装配体接触条件受制于其他用户定义的零部件接触条件,而所有零部件接触都受制于局部接触条件。

选择接触类型为“无穿透”,依次选择如下图所示的两个面。

4.划分网格,使用默认单元大小对模型划分网格,勾选“自动过渡”。网格划分完成之后如下图所示。
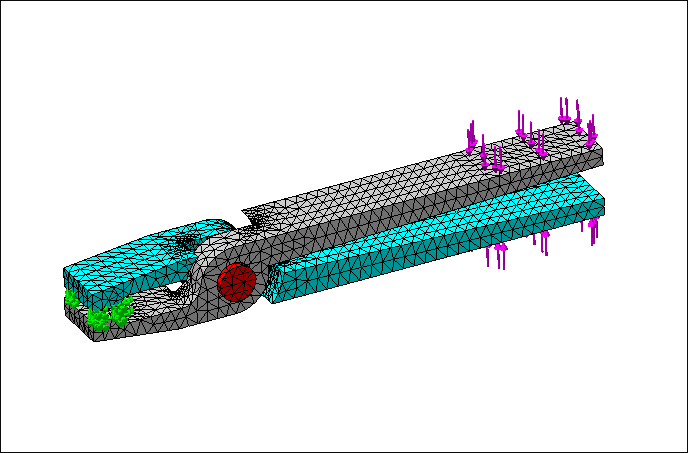
5.运行分析。
点击“No”,以线性的方式完成分析。

我们可以观察到最大的von Mises应力值为2245MPa,当然这个值是不真实的。材料屈服表明线性分析不再有效,需要采用非线性分析。

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-05-05
最近编辑:1年前
还没有评论
相关推荐
最新文章
热门文章




