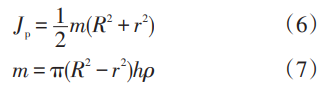【摘 要】针对航空发动机的转子/整机动力学问题,使用两自由度动力学模型对转、静子的振动耦合机理进行了解释,指出传统转子动力学模型将导致最大67%的计算误差,因此需要采用整机动力学模型对发 动机的振动特性进行求解。进一步明确了整机动力学有限元模型的简化原则和模型功用,针对转、静子的 典型结构论述了详细的建模方法。采用整机三维模型对双转子涡扇发动机的固有振动特性进行了计算和评估,结果表明,慢车至最大转速区间内只存在一阶高压转子平动振型,转子系统总应变能不超过20%,共 振裕度大于20%,满足航空发动机的转子动力学设计要求。
DOI: 10.13675/j.cnki.tjjs.2015.05.017
【关键词】转子动力学;整机振动;有限元;临界转速
与地面燃气轮机相比,现代航空发动机的一个典型特点是转子系统与静子系统的刚度接近,因而转静子之间的振动耦合问题突出。不能够准确合理的考虑静子刚度、质量特征对转子振动特性的影响,将带来转子临界转速、不平衡响应等计算结果的较大误差。虽然可以采用支承动刚度对此问题进行近似考虑,但临界转速附近的振动响应求解不准确, 同时无论采用测试方法还是数值仿真计算,都很难 获得真实发动机各支点的动刚度值。为避免上述问题,航空发动机设计中可采用梁单元对涡扇发动机建立整机动力学分析模型,其中机匣被等效为零转速的转子 。陈果,Philip利用梁单元建立了整机动力学模型,并计入了滚动轴承和挤压油膜阻尼器的非线性,获得了整机模态特征。但基于梁单元的有限元模型却存在如下局限性:①高压压气机的大直径鼓筒并不满足长径比足够大的梁单元假设,会带来弯曲模态频率求解误差偏大;②不能精确刻划转子中锥形壳体的质量和刚度沿轴向的变化;③不能考虑离心预应力的刚度增 强效应。因此近年来国外均发展了整机的三维动力学模型建立与分析方法。Romuald采用三维壳单元整机模型对 EJ200涡扇发动机的振动响应等问题进行了计算,并与台架试车结果进行了对比。Jose, Garcia针对航空发动机的建模方法进行了系统的研究,并采用整机三维壳体模型对其在冲击载荷下的振动响应特征进行了分析。本文使用两自由度动力学模型对航空发动机中转、静子的振动耦合机理进行解释,并给出整机动力学模型的建立方法和功用,最后通过算例给出顺转 双转子发动机的临界转速确定方法。航空发动机系统由于转子系统的刚度、质量与静子系统相接近,因此需要采用整机模型对其振动特性进行求解,否则将带来不可接受的误差。对于此误差的产生机理,可使用如下力学模型给予类别分析和说明。转子轴系通过弹性支承与静子系统相连接,如图1所示。其对应力学模型如图2所示,图中m1为转子轴系总质量;k1为弹性支承的刚度;m2为静子系统质量;k2为静子系统刚度。其中图 2(a)为耦合模型, 对应于整机动力学模型;图 2(b)为独立模型,对应于传统的转子动力学模型。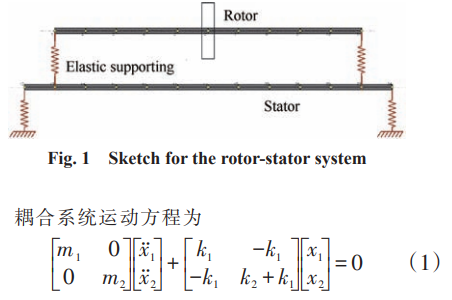

由于式(2)(3)的结果不够直观,下面对两种假设情况进行对比。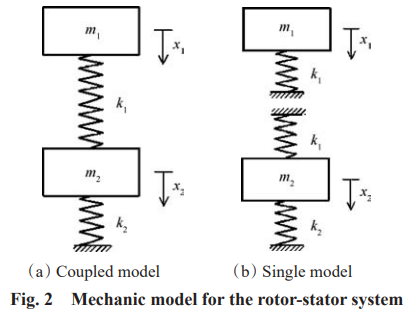
对于地面旋转机械 k2>> k1,m2>> m1,可假设 k2=100k1,m2=m1,则有式(4),可见对于转子的固有频率 ω1 ,采用两种模型获得的结果相差很小,相对误差为 5%。
由上述分析可知,只有使用整机动力学模型,才可以准确地获得航空发动机转子系统的固有频率, 才可以进一步准确地求解转子系统临界转速。采用实体单元模型可以更为准确地描述航空发动机转静子系统的复杂结构特征,但必须进行适当合理的等效简化。其一是由于发动机结构复杂,如果过于考虑圆角、小孔等细节因素,将导致所建立的模型自由度过多,计算经济性差,甚至无法完成计算。其二是由于目前的有限元软件中固有模态求解模块是无法对局部振动和整体振动进行区分的,因而会导致计算结果中局部模态过于丰富,使转子/整机振动模态被盘片耦合等局部振动模态所湮没, 很难完成关心模态的提取工作。因此,在整机动力学模型建立中,必须大幅度的简化以控制模型的自由度数。为保证动力学特征的准确性,应重点保证模型质量、刚度与实际结构的相 似性 。具体而言,①应保证模型的质量分布与实际结构相似,尤其是质量沿轴向的分布特征、重心位置;②应保证转动惯量的分布与实际结构相似,尤其 是转子轴系的转动惯量的轴向分布特征;③抗弯刚度的分布相似。 整机动力学有限元模型并非适用于所有的强度、振动问题,追求功用过多只会导致模型自由度过大,无法完成计算。本文方法所建立的模型重点在于实现如下功用:①可以准确考虑转/静子之间的振动耦合,获得更为准确的转子临界转速以及发动机整机振动特性。②可为部件计算提供准确的边界条件。整机动力学模型不能考虑圆角、小孔等局部细节对应力分布的影响,本身并不 适用于静强度分析。但根据子模型原理,可以根据其计算获得的位移分布为部件计算提供准确的边界条件定义。④为安装节设计与飞发协调设计提供准确的等效模型和载荷条件。在飞机总体设计中是将发动机作为质量块和激励参数处理的,应用整机模型可以计算得到各种工况下的外传力大小及频率特征,提供准确的飞发载荷。⑤可用于计算发动机转/静子轴向力,获得机匣载荷的准确分布特征,为发动机总体结构中传力路线的设计提供技术支撑。下面以 ANSYS 通用有限元程序为例,对航空发动机典型结构建模方法进行详细论述。叶盘结构是航空发动机转子轴系的主要部件, 一些文献在叶片处理上,将其直接等效为集中质量单元,而轮盘使用实体单元,由于不同单元类型的节 点自由度不同,因此将带来转动惯量的误差,高压压气机叶片较小,此影响不大,而风扇/涡轮叶片,其影响很大。在整机三维动力学模型中,建议采用等效环处理方法,以准确考虑各级叶片转动惯量的动力学影响,并且可以降低自由度和剔除盘片耦合振动。等效环处理方法是在轮盘外圈建立一个圆环结构以模拟叶片对转子横向振动的影响。所建立等效圆环的极转动惯量 Jp和总质量 m 如式(6)和(7)所示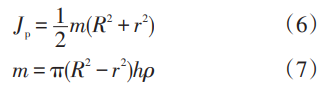
式中 r 是等效圆环的内径,由轮盘实际外缘半径 确定;R 是等效圆环外径,由叶片长度确定;h 是等效 圆环的厚度,ρ是等效圆环密度。所建立圆环的 Jp和 m 应与实际结构整圈叶片的数值相同,因此联立式(6)和(7)可求得等效环的关键参数:厚度 h 和密度 ρ 。据此可在各级轮盘外缘建立等效环。套齿连接结构是低压转子系统常用的连接方式,横向载荷、定位面配合紧度、预紧力、定位间距和接触面积等诸多参数都对套齿结构的连接刚度存在 影响,进而影响整个转子的动力学特性。采用 接触模型虽然可以准确考虑套齿结构的刚度影响, 但无法应用于整机模型。整机有限元模型中,可使用当量刚度方法,即首先采用接触模型获得套齿连接刚度的关键影响参数和影响规律,再根据实际工作状态,确定当量刚度值,在模型中通过修改套齿材料弹性模量参数的方法,以获得相应的当量刚度值。在ANSYS 中可采用 COMBIN14 模拟一般的线性支承单元,采用 COMBIN40 模拟带有间隙的支承,采用 COMBIN214 模拟随转速变化支承刚度的支承,即 COMBIN214 可以对转子支承的动刚度进行模拟。值得注意的是,在整机动力学模型中,无论采用哪种单元,其刚度应为鼠笼或弹性环等弹性支承的刚度;而在传统的转子动力学模型中,COMBIN 单元应为“弹性支承+承力机匣”的串联刚度,以降低转子振动特 性的求解误差。类似涡轮导向叶片的搭接、销接等柔性连接结构,在 ANSYS 中可使用 MPC184 多点约束单元来对其力学影响进行等效;静子叶片可采用集中质量法或前文提到的等效圆环法,关键是准确考虑叶片质量对静子动力特性的影响;幅板结构,可参考文献提出的简化原则,保证简化前后的横截面积不变,弯曲刚度不变,剪切模量不变,沿纵向的质量分布不变;类似火焰筒的带小孔结构,可直接忽略小孔对振动特性的影响;附件系统可采用子结构法来考虑其刚度和质量对机匣的动力特性影响。某双转子涡扇发动机的总体结构简图如图3所示,高、低压转子同向旋转,高压转子支承于 3 号和 4 号支点,其中 4 号为中介支点,低压转子支承于 1 号、 2 号和 5 号支点。对其采用八节点六面体实体单元建立整机动力学有限元模型,总自由度数为 621,280, 其中转子系统自由度数为 211,630。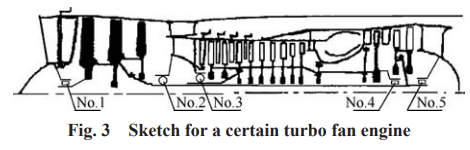
采用 ANSYS固有模态求解模块,代入高低压转速关系,考虑陀螺力矩的影响,获得转子振动为主的各阶模态正、反进动随低压转速变化曲线如图 4 所示。可见,由于高低压转子之间以及与静子系统的振动耦合影响,转子振动的动频曲线非常密集,各阶振动随转速变化规律也各不相同。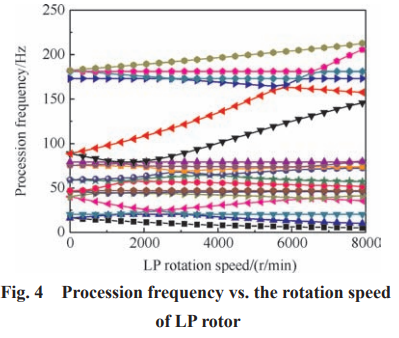
在图 5 基础上进一步绘制转子不平衡激励随转速的变化曲线 ,即可以求 得双转子系统的临界转速。值得注意的是:①由于此发动机为顺转转子,因 此高、低压不平衡激励只能激起系统的正进动临界转速,在图 4 中所有反进动曲线可以被剔除。②航空发动机的转子动力学设计中,主要关心的是不平衡激励引起的转子横向振动,因此在临界转速求解时, 轴向振动和扭转振动可以被剔除。轴向振动由于不受陀螺力矩的影响,因此在图 5 中,其动频曲线特征是不分叉的,并且随转速增加基本不变。③由于两个转子通过中介轴承相连,高压的不平衡激励将通过中介支点传至低压转子,反之亦然。因此在 Camp⁃ bell 图绘制中,需要同时考虑高、低压转子的不平衡 激励。综合考虑上述因素,代入高低压转速关系曲线, 绘制 Campbell 图如图 5 所示。图中,n=1,…,7 为转 子系统的各阶正进动频率曲线;低压激励为一条射线,其与各阶正进动曲线的交点即为低压转子激起的临界转速,如图中圆点所示。由于发动机主要工作于慢车至最大转速区间,因此临界转速点 A 应给与重视,求得在慢车转速工作时,其共振裕度为21.1%, 在巡航转速工作时,其共振裕度为 22.3%,满足大于 20%的临界转速裕度设计要求。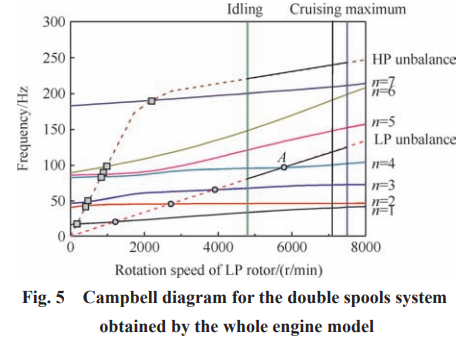
图 5 中高压激励为一条复杂变化的曲线,由高低压转速匹配关系所决定。其与各阶正进动曲线的交点为高压转子激起的临界转速,如图 5 中方块所示。对此发动机而言,在启动过程中将快速通过多阶高压激起临界转速,但在慢车至最大转速区间,并不存在临界转速,并且在各稳定转速工况,满足大于 20% 的裕度要求。 对于临界转速点 A,给出其临界转速振型如图 6 所示,可见,此阶临界转速对应振型以高压转子为主(平动),而低压转子风扇段基本没有变形,只是涡轮段略有平动,整体而言属于转子的刚体振型。在该振型下,整机应变能分布如图 7 所示。高压压气机前支点的应变能最大,即图 3 中的 3 号支点,达到了整个系统应变能的 50%以上,而高压转子本身的应变能较小,占系统的15%左右,在 3 号支点处合理设计支承刚度和阻尼结构是振动抑制的有效措施。总体而言,发动机的应变能主要集中于静子系统,而转子系统的总应变能不超过 20%,因此发动机虽然变转速工作,反复通过临界转速点 A,但不会引 起转子轴系的有害应变积累,满足航空发动机对临界转速点的应变能设计要求。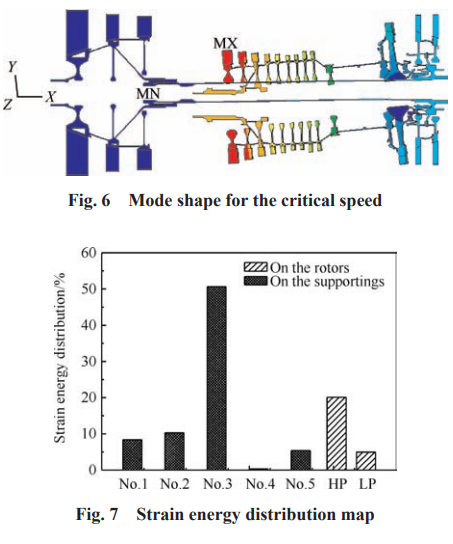
前文给出了采用整机模型获得的低压转子激起 临界转速值(5770r/min)。如果将静子系统考虑为支 点静刚度,采用传统的转子动力学模型求解,最终获得 Campbell 图如图 8 所示,对应低压转子激起临界转 速为 7243r/min,两者相对误差为 25.5%。工程实践表明,整机模型的计算结果具有更高的精度。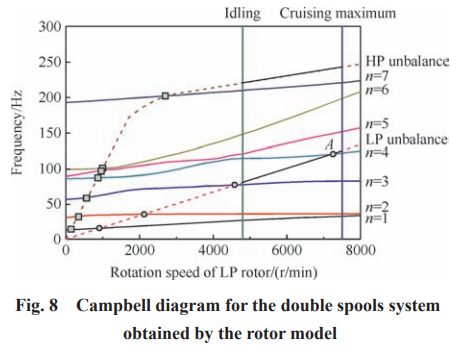
航空发动机由于转、静子刚度接近,传统转子动力学模型将导致最大 67%的固有模态频率的计算误差,因此需要采用整机动力学模型对发动机的临界转速进行计算分析。双转子涡扇发动机的高、低压转子不平衡激励 可能激起转子系统的多阶临界转速,但在慢车至最大转速区间内只存在一阶高压平动振型,并且在各 转速工况均满足大于 20%的共振裕度要求。对应的应变能分布主要集中于静子系统,而转子系统的总应变能不超过 20%,因此在发动机反复通过临界转 速点 A 的工作过程中,不会引起转子轴系的有害应变积累。