汽车动力总成悬置支架的多目标拓扑优化
【摘要】汽车动力总成悬置支架设计是一个静动态多性能指标的优化过程。为克服单目标拓扑优化的局限性,以静态多工况下刚度和动态特征值为性能指标,采用折衷规划法定义目标函数,构建多目标连续体结构拓扑优化数学模型,进行悬置支架多目标拓扑优化。依据拓扑优化结果并考虑制造工艺性等要求,对悬置支架进行详细设计。最后对支架设计模型进行强度校核、模态仿真分析和耐久性试验验证,结果表明,采用所提出的方法进行悬置支架的概念设计可行且有效。
【关键词】发动机悬置支架;拓扑优化;多目标优化;折衷规划法 汽车动力总成悬置支架是动力悬置系统的重要安全件和功能件。其主要功用为:可靠地连接发动机(或变速器)与车身(或副车架),传递各种行驶工况下作用在动力总成上的力和力矩,有效地隔离动力总成工作过程中产生的各种振动和冲击。因此, 进行动力总成的悬置支架设计时,应综合考虑悬置支架的强度、刚度、固有频率、耐久性和轻量化等性能指标要求,属于典型的多目标优化问题。 文献《关于某动力总成悬置支架的优化设计》中针对某工况下受发动机频率激振影响,支架发生共振问题,对支架结构进行模态性能优化设计,有效降低了车内噪声和振动。文献《动力总成悬置支架的多工况拓扑优化》中采用多工况拓扑优化方法,以最小加权柔度为目标, 辅以模态、应力和体积为约束,进行动力总成悬置支架改进设计,有效改善其各项性能指标。文献《动力总成悬置支架拓扑优化研究》中基于模态固有频率的结构拓扑优化方法,对动力总成悬置支架进行优化设计,为后续详细设计提供了良好的基础。文献《基于有限元技术的动力总成悬置支架拓扑优化的研究》中在悬置系统动力学仿真分析的基础上,对悬置支架进行结构拓扑优化。文献《考虑工程约束的发动机悬置支架拓 扑优化》中分别进行多工况下加权柔度最小化和频率最大化的单目标拓扑优化设计,并考虑工程约束条件,进行支架的结构性能优化,为其轻量化和力学性能改善提供了新的设计思路,但并未进行多目标性能综合拓扑优化。 本文中在产品概念设计阶段将拓扑优化技术引入到动力总成悬置支架的结构设计中,按照设计空间建立拓扑优化区域,确定动力总成悬置支架多种行驶工况下所受载荷,并综合考虑制造工艺性约束条件,构建多目标拓扑优化模型,涉及静态多工况刚度和动态特征值性能指标,根据拓扑优化结果重构动力总成悬置支架的详细结构,最后对新结构进行必要的仿真分析和试验验证。 为研究动力总成悬置系统的受力情况,需要建立力学模型和数学模型,动力总成悬置系统为多自由度振动系统,利用 ADAMS建立车辆动力总成系统动力学模型,同时综合考虑动力总成悬置橡胶衬套的刚度、动力总成质量、质心位置、转动惯量、变速器速比、发动机转矩和转速等因素,求解并输出动力总成在各悬置弹性中心点的载荷。 为考虑动力总成系统在多种工作状况下对悬置结构的影响,本文中采用GM动力总成悬置系统载荷计算方法,获得动力总成悬置在多工况下的载荷, 各种工况下悬置支架所受载荷工况如表1所示。 在进行结构拓扑优化设计前,根据设计要求和悬置支架的结构特点确定初始设计空间,需要综合考虑支架与其他部件之间的装配关系、装配路径和静动态干涉约束确定合理的设计区域与非设计区域 (见图1)。其中,支架通过螺栓与变速器体和橡胶衬套与副车架的连接区域设置为非设计区域。 进行结构拓扑优化过程中,依然面临数值不稳定现象,如棋盘格格式和网格依赖性等问题。为有效抑制数值不稳定问题的出现,施加最小成员尺寸约束,保证良好拓扑结果构型,从而得到比较均匀的材料分布方案。对于铸造结构,必须考虑制造加工过程中的拔模方向,保证结构具有良好的加工特征,在拓扑优化过程中添加拔模方向约束见图2。 结构静力学拓扑优化是研究在设计域内得到使结构柔度最小(即刚度最大) 的材料分布形式的问题。而悬置支架在不同的行驶工况下承受不同的载荷工况,因此其静力学拓扑优化为典型的多个工况下的刚度拓扑优化问题,称为多刚度拓扑优化问题。针对各个典型载荷工况所对应的目标性能分别赋予权系数,由折衷规划法定义悬置支架平均柔度目标函数,其静态多工况刚度拓扑优化数学模型如下: 式中:ρ 为设计变量向量;N为设计区域单元总数;m为悬置支架所受载荷工况总数;  为第k个载荷工况的权系数;
为第k个载荷工况的权系数; 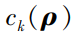 为第k个工况的柔度值;
为第k个工况的柔度值;  为单元体积;
为单元体积;  与 f 分别为设计区域体积与体积分数,设定f=50%;K,U 和F分别为结构的整体刚度矩阵、节点位移矢量和载荷矢量;本文中假定各个目标具有相同的重要程度,设定
与 f 分别为设计区域体积与体积分数,设定f=50%;K,U 和F分别为结构的整体刚度矩阵、节点位移矢量和载荷矢量;本文中假定各个目标具有相同的重要程度,设定  ;q为惩罚因子,q≥2;
;q为惩罚因子,q≥2; 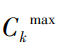 和
和  分别为第k个工况单独进行优化时柔度的最大值和最小值。 对于悬置支架结构的动态振动频率拓扑优化, 通常选取低阶频率的最大化作为优化目标函数,为克服频率目标函数出现的振荡现象,保证拓扑优化过程的稳定性。本文中采用平均特征值定义悬置支架动力学拓扑优化的目标函数,其数学模型为 式中:h为悬置支架需要优化的特征值阶次;
分别为第k个工况单独进行优化时柔度的最大值和最小值。 对于悬置支架结构的动态振动频率拓扑优化, 通常选取低阶频率的最大化作为优化目标函数,为克服频率目标函数出现的振荡现象,保证拓扑优化过程的稳定性。本文中采用平均特征值定义悬置支架动力学拓扑优化的目标函数,其数学模型为 式中:h为悬置支架需要优化的特征值阶次;  为第i阶特征值;
为第i阶特征值;  与 α 为给定参数;
与 α 为给定参数; 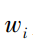 为第i阶特征值的权系数;
为第i阶特征值的权系数;  为设计区域有限元模型的总自由度数。本文中取前6阶特征值作为目标函数,对应的权系数设定为
为设计区域有限元模型的总自由度数。本文中取前6阶特征值作为目标函数,对应的权系数设定为  ,参数
,参数  , f=50%。 进行悬置支架的多目标拓扑优化时,需要同时考虑静态刚度目标和动态特征值目标的拓扑优化, 在满足结构刚度足够大的同时,使动态的固有频率足够高,这样结构才具有良好的静态特性和动态特性。多目标优化设计面临两个难题:①目标函数量级不同;②优化目标帕累托集求解。本文中采用折衷规划法,预先进行单目标问题求解,获取最优值, 称为理想点;采用归一化方法与最短距离理想点法, 构造加权目标函数,寻找与理想点距离最小的可行点,也称为“最优妥协解” 。由折衷规划法可得到悬置支架的多目标拓扑优化数学模型: 式中:
, f=50%。 进行悬置支架的多目标拓扑优化时,需要同时考虑静态刚度目标和动态特征值目标的拓扑优化, 在满足结构刚度足够大的同时,使动态的固有频率足够高,这样结构才具有良好的静态特性和动态特性。多目标优化设计面临两个难题:①目标函数量级不同;②优化目标帕累托集求解。本文中采用折衷规划法,预先进行单目标问题求解,获取最优值, 称为理想点;采用归一化方法与最短距离理想点法, 构造加权目标函数,寻找与理想点距离最小的可行点,也称为“最优妥协解” 。由折衷规划法可得到悬置支架的多目标拓扑优化数学模型: 式中:  和
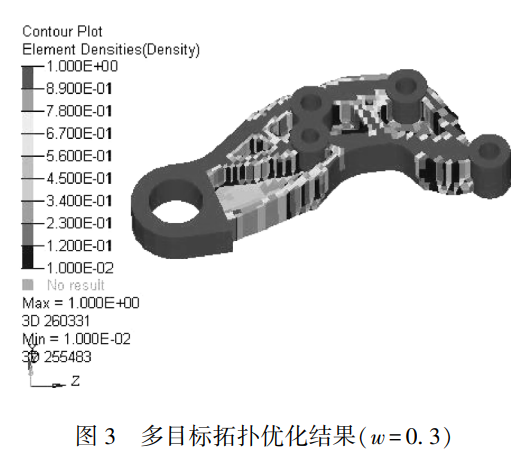
和  分别为单独进行动力学特征值优化时的最优值与初值;w为权系数,取值区间为[0,1]。 经过优化迭代,悬置支架多目标拓扑优化结果汇总于表2。当w=0.3时获得最优妥协解,最优拓扑构型如图3所示。此时,支架拓扑优化结构在保证最优传力路径的基础上,兼顾优化结构的振动特性,实现了结构的静力学多刚度和动力学特征值的协同优化设计。 依据上述多目标拓扑优化结果分析,同时参考悬架结构设计特点并结合制造工艺性约束条件,根据材料分布形式进行了概念提取,支架的结构概念设计基本按照拓扑优化结构来布置。对于铸铝件, 考虑铸造工艺要求,其厚度尺寸取为5mm,最小开孔尺寸为10mm,结构的最终设计综合考虑这些要素。另外,高度方向因装配要求未做参数化设计。经详细设计后的悬置支架结构几何模型和实物如图4所示。 悬置支架设计完成后,必须对其进行必要的强度、模态分析和实物台架耐久性试验验证。验证产品结构设计的合理性。 悬置支架采用铸铝ALSi9Cu3进行高压铸造,弹性模量E=72.5GPa;泊松比 μ =0.33;密度ρ=2.7×
分别为单独进行动力学特征值优化时的最优值与初值;w为权系数,取值区间为[0,1]。 经过优化迭代,悬置支架多目标拓扑优化结果汇总于表2。当w=0.3时获得最优妥协解,最优拓扑构型如图3所示。此时,支架拓扑优化结构在保证最优传力路径的基础上,兼顾优化结构的振动特性,实现了结构的静力学多刚度和动力学特征值的协同优化设计。 依据上述多目标拓扑优化结果分析,同时参考悬架结构设计特点并结合制造工艺性约束条件,根据材料分布形式进行了概念提取,支架的结构概念设计基本按照拓扑优化结构来布置。对于铸铝件, 考虑铸造工艺要求,其厚度尺寸取为5mm,最小开孔尺寸为10mm,结构的最终设计综合考虑这些要素。另外,高度方向因装配要求未做参数化设计。经详细设计后的悬置支架结构几何模型和实物如图4所示。 悬置支架设计完成后,必须对其进行必要的强度、模态分析和实物台架耐久性试验验证。验证产品结构设计的合理性。 悬置支架采用铸铝ALSi9Cu3进行高压铸造,弹性模量E=72.5GPa;泊松比 μ =0.33;密度ρ=2.7×  ;屈服极限
;屈服极限  =120MPa;抗拉强度UTS=270MPa。由于零件失效往往从表面开始,所以对悬置支架划分网格后,支架的网格模型外部还需包络一层壳单元,单元平均尺寸为3mm,其对应的厚度为
=120MPa;抗拉强度UTS=270MPa。由于零件失效往往从表面开始,所以对悬置支架划分网格后,支架的网格模型外部还需包络一层壳单元,单元平均尺寸为3mm,其对应的厚度为  ,对悬置支架进行各种载荷工况下的应力应变分析,结果如表3所示。 由计算结果可知,悬置支架最危险的工况为13号载荷工况。从支架的应力计算结果来看,其常用工况最大应力低于材料屈服3倍正态分布 σ 值,极限工况下支架表面应力低于材料屈服应力,故该支架完全满足强度设计要求。悬置支架的固有频率对悬置系统的振动有较大的影响,因此需要对支架进行模态分析,约束状态下的固有频率计算列于表4。从模态分析结果来看, 悬置支架1阶固有频率已经达到851Hz,超过了动力总成系统要求的最低600Hz的要求,支架在结构性能上已达到设计要求。 悬置支架耐久性试验主要验证结构的疲劳可靠性能。试验台的设备包括刚性台、液压作动缸、位移和力传感器。 支架的疲劳试验台架如图5所示,该台架试验下的支架载荷为幅值8500N 的正弦波,加载频率为3~5Hz。设计要求50万次寿命,为使支架在该载荷下满足50万次寿命的可靠性达到99%,按照数理概率统计学原理,必须做完3倍的50万次循环而不发生失效。支架疲劳台架试验寿命结果列于表5。结果表明,悬置支架满足耐久性指标。 1.提出并构建悬置支架的静动态多目标拓扑优化数学模型,以静态多工况下刚度和动态特征值为性能指标,采用折衷规划法定义目标函数,实现支架的多目标拓扑优化,保证了结构具有良好的静动态性能。 2. 依据多目标优化最优妥协解,对悬置支架进行详细设计,结构满足强度和耐久性设计要求,提高了产品的可靠性,且固有频率避开动力总成的激振敏感区域,有效解决了共振问题。 3.基于多目标拓扑优化技术的产品结构概念设计,在性能上保证了设计要求,为后续结构详细设计提供依据,缩短了设计开发周期,为实现车辆的轻量化设计提供有效的解决方案。 【免责声明】本文来自悬置空间,版权归原作者所有,仅用于学习等,对文中观点判断均保持中立,若您认为文中来源标注与事实不符,若有涉及版权等请告知,将及时修订删除,谢谢大家的关注!
,对悬置支架进行各种载荷工况下的应力应变分析,结果如表3所示。 由计算结果可知,悬置支架最危险的工况为13号载荷工况。从支架的应力计算结果来看,其常用工况最大应力低于材料屈服3倍正态分布 σ 值,极限工况下支架表面应力低于材料屈服应力,故该支架完全满足强度设计要求。悬置支架的固有频率对悬置系统的振动有较大的影响,因此需要对支架进行模态分析,约束状态下的固有频率计算列于表4。从模态分析结果来看, 悬置支架1阶固有频率已经达到851Hz,超过了动力总成系统要求的最低600Hz的要求,支架在结构性能上已达到设计要求。 悬置支架耐久性试验主要验证结构的疲劳可靠性能。试验台的设备包括刚性台、液压作动缸、位移和力传感器。 支架的疲劳试验台架如图5所示,该台架试验下的支架载荷为幅值8500N 的正弦波,加载频率为3~5Hz。设计要求50万次寿命,为使支架在该载荷下满足50万次寿命的可靠性达到99%,按照数理概率统计学原理,必须做完3倍的50万次循环而不发生失效。支架疲劳台架试验寿命结果列于表5。结果表明,悬置支架满足耐久性指标。 1.提出并构建悬置支架的静动态多目标拓扑优化数学模型,以静态多工况下刚度和动态特征值为性能指标,采用折衷规划法定义目标函数,实现支架的多目标拓扑优化,保证了结构具有良好的静动态性能。 2. 依据多目标优化最优妥协解,对悬置支架进行详细设计,结构满足强度和耐久性设计要求,提高了产品的可靠性,且固有频率避开动力总成的激振敏感区域,有效解决了共振问题。 3.基于多目标拓扑优化技术的产品结构概念设计,在性能上保证了设计要求,为后续结构详细设计提供依据,缩短了设计开发周期,为实现车辆的轻量化设计提供有效的解决方案。 【免责声明】本文来自悬置空间,版权归原作者所有,仅用于学习等,对文中观点判断均保持中立,若您认为文中来源标注与事实不符,若有涉及版权等请告知,将及时修订删除,谢谢大家的关注! 著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-03-20
最近编辑:2年前

硕士
|
CAE仿真负责人
个人著作《汽车NVH一本通》
获赞 1176粉丝 6591文章 1024课程 20




 为第k个载荷工况的权系数;
为第k个载荷工况的权系数; 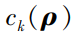 为第k个工况的柔度值;
为第k个工况的柔度值;  为单元体积;
为单元体积;  与 f 分别为设计区域体积与体积分数,设定f=50%;K,U 和F分别为结构的整体刚度矩阵、节点位移矢量和载荷矢量;本文中假定各个目标具有相同的重要程度,设定
与 f 分别为设计区域体积与体积分数,设定f=50%;K,U 和F分别为结构的整体刚度矩阵、节点位移矢量和载荷矢量;本文中假定各个目标具有相同的重要程度,设定  ;q为惩罚因子,q≥2;
;q为惩罚因子,q≥2; 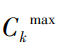 和
和  分别为第k个工况单独进行优化时柔度的最大值和最小值。
分别为第k个工况单独进行优化时柔度的最大值和最小值。 
 为第i阶特征值;
为第i阶特征值;  与 α 为给定参数;
与 α 为给定参数; 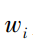 为第i阶特征值的权系数;
为第i阶特征值的权系数;  为设计区域有限元模型的总自由度数。本文中取前6阶特征值作为目标函数,对应的权系数设定为
为设计区域有限元模型的总自由度数。本文中取前6阶特征值作为目标函数,对应的权系数设定为  ,参数
,参数  , f=50%。
, f=50%。 
 和
和  分别为单独进行动力学特征值优化时的最优值与初值;w为权系数,取值区间为[0,1]。
分别为单独进行动力学特征值优化时的最优值与初值;w为权系数,取值区间为[0,1]。 

 ;屈服极限
;屈服极限  =120MPa;抗拉强度UTS=270MPa。由于零件失效往往从表面开始,所以对悬置支架划分网格后,支架的网格模型外部还需包络一层壳单元,单元平均尺寸为3mm,其对应的厚度为
=120MPa;抗拉强度UTS=270MPa。由于零件失效往往从表面开始,所以对悬置支架划分网格后,支架的网格模型外部还需包络一层壳单元,单元平均尺寸为3mm,其对应的厚度为  ,对悬置支架进行各种载荷工况下的应力应变分析,结果如表3所示。
,对悬置支架进行各种载荷工况下的应力应变分析,结果如表3所示。 







