【JY】SAP2000中目标位移法的找形分析功能
本文摘要(由AI生成):
本文介绍了使用SAP2000软件对三种不同类型张力结构(索杆结构、穹顶结构和环形张力索结构)进行找形分析的过程。通过迭代计算,确定了结构在自重作用下的预应力分布,并与已有研究进行了对比,验证了结果的准确性。文章展示了SAP2000在处理张力结构找形问题中的有效性和精确性,强调了目标位移法在该类问题中的应用价值。
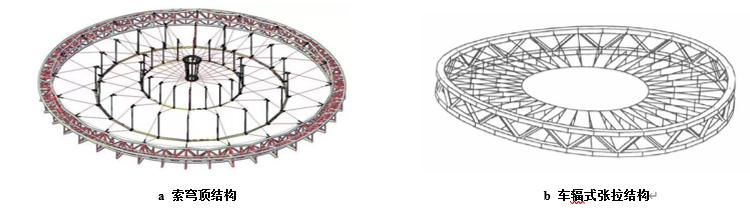
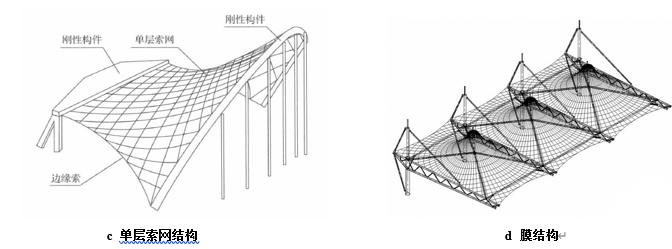
1.基本原理介绍
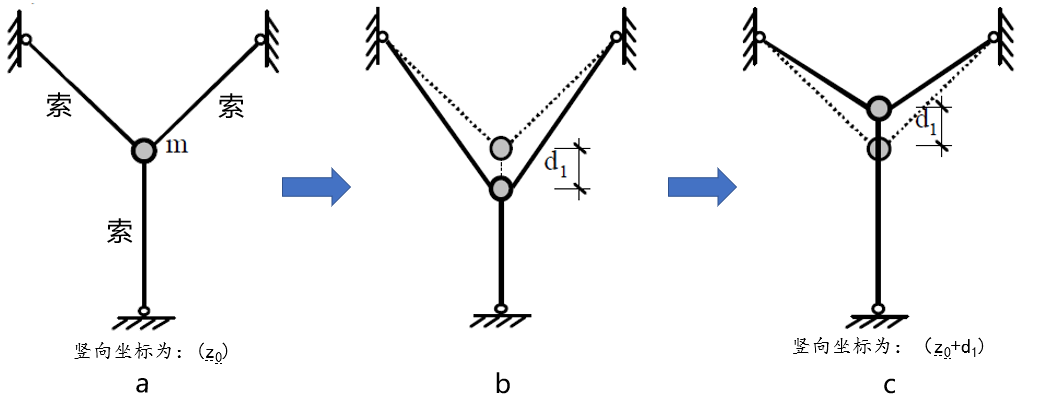

图2 目标位置法计算示意图
1.2 SAP2000中的目标位移法
基于上述原理,SAP2000中嵌入了目标位移法。在分析完成后,通过命令:分析>修改未变形几何,可以打开下图对话框,其中【几何修改选项】中的“目标位移法-节点坐标减去节点位移”即为目标位移法。

图3 SAP2000中目标位移法
该选项中的【荷载工况】为施加找形时需考虑的荷载工况。如上图中,在找形时仅需要考虑结构的自重,因此荷载工况设置为“DEAD”。在该工况中,程序会计算各个控制节点的位移,通过当前工况的节点坐标,节点的原始坐标,放大系数,即可求出下次迭代时节点的新坐标,计算方法为:节点的新坐标 = 当前工况的节点坐标+放大系数×(原始坐标-(当前工况的节点坐标+当前工况下的节点位移),相应的计算公式为:
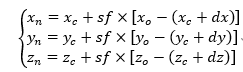
其中:放大系数sf,用于控制新节点坐标偏移当前工况节点坐标的程度,程序默认值1。放大系数取1时,以z坐标为例,此时公式即可退化为:
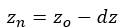
与图2-e 中的坐标表达式基本相同。
计算出各个控制点的新的坐标位置后,在【方向和位置】选项卡中,用户可以选择是否修改所有节点的坐标,还是仅修改部分节点。另外用户也可以仅修改控制节点的某个方向的坐标,一般建议保持默认全选。
通过修改未变形几何调整节点初始坐标后,然后再次运行分析工况。分析完成后程序会输出节点的目标坐标、实际坐标和百分比差异(%差异),如下图所示。其中“目标坐标”为节点的原始坐标,“实际坐标”为当前工况下节点变形后的坐标。“%差异”表示上一步修改未变形几何时施加的节点坐标修改数值di,与当前工况中的节点的位移di+1的差值百分比,即(di+1-di)/di。通过查看“实际坐标”或“%差异”,可以判断当前结果是否满足要求。当“节点实际坐标”和“目标坐标基本”相同或“%差异”接近0时,即表示结构已达到目标状态,此时的预应力分布即为找到的力。
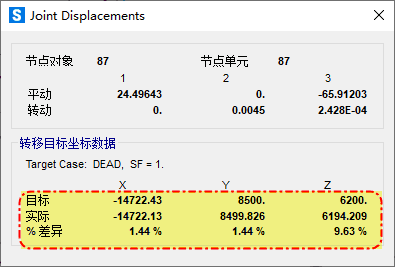
图4 节点位移输出
SAP2000中目标位移法的整个计算过程可通过下侧流程图来表示:
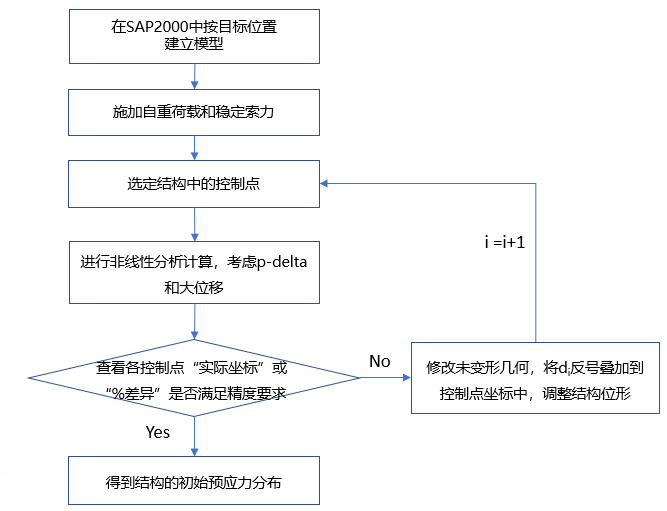
图5 目标位移法流程图
2.功能说明算例
现在通过图6中的索撑杆模型[2]来介绍在SAP2000中如何通过目标位移法对该结构进行找形分析。该模型是由6根索和2 根撑杆组成,其中7号、8号杆件为撑杆,其余构件均为相同截面的索。索截面半径为3mm,弹性模量E=1.8×105MPa,热膨胀系数α=1.2×10-5;杆截面面积为7.0686mm2,弹性模量E=2.06×105MPa,热膨胀系数α=1.2×10-5。索和撑杆的材料密度均为7850kg/m3。现在需要计算该结构在自重作用下,各段索需要施加多大的索力才能在设计位置处保持平衡。
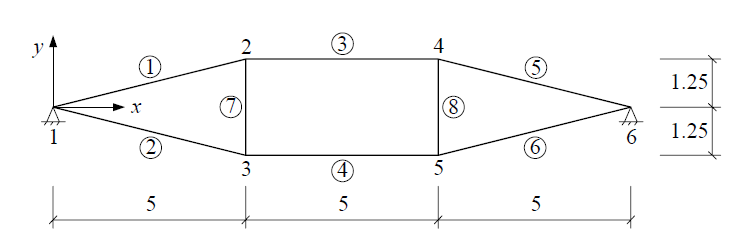
图6 索撑杆模型
2.1 模型建立
首先在SAP2000中建立上述模型。注意,建模时撑杆采用框架单元模拟,索采用索单元模拟。在定义索的初始几何信息时,需要给索施加一个初始的张拉力,使索在绘制的时候就存在一定的张力。施加初始张力是为了保证索在开始计算阶段即存在一定的刚度,如果开始计算时索刚度较小,会导致结构的在荷载作用的变形过大,容易出现不收敛的问题。为保证整个结构在初始张力下的变形与目标位置的偏差不至于过大,可以将每个索的无应力索长设为索两端点之间距离的n倍(n<1)。
对于该模型可以通过“索-相对未变形长度”定义索单的几何信息,以5号索为例,其相对长度设置为0.9993。如图7所示,可以看到该索在绘制时,索对应 i 段的张力为4228.8067N。该索力可以理解为将长度为5154.0333*0.9993=5150.2952mm的索拉长到了5154.0333mm,挂在了4号和6号节点之间,此时4号节点端索张力为4228.8067N,6号节点端索张力为4226.0848N。但是通过这种方式施加的张力拉力并不是一个平衡索力,后续工况中该索的索力会根据结构的变形协调而改变,这里仅是为了给索提供一个初始刚度。
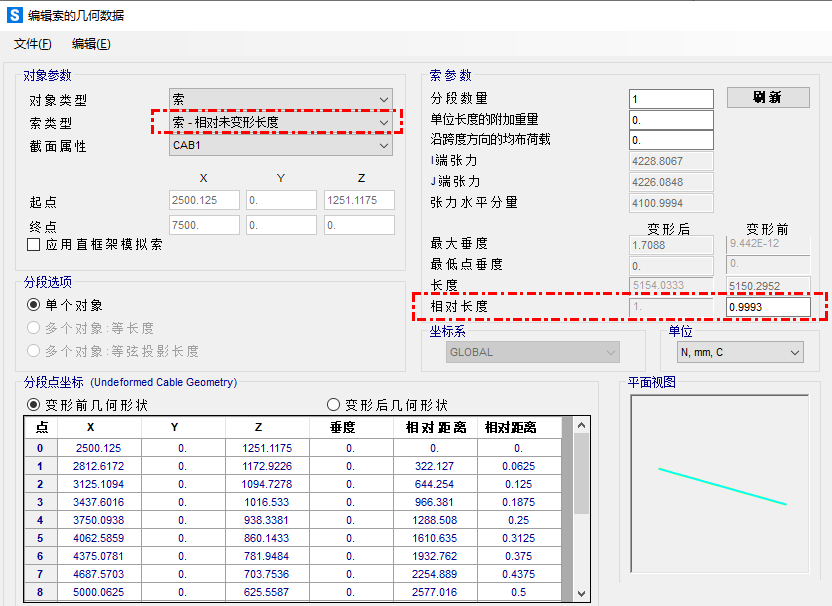
图7 索初始几何信息的指定
2.2 工况设定
该模型需要找到在自重作用下该结构在建模位置处达到平衡的合适索力,因此在荷载工况中仅需要考虑自重。这里不用对索施加额外的索力,索力会通过目标位移法迭代得到。由于索结构一般比较柔,变形较大,因此在分析时需要勾选P-delta和大位移效应,工况设置如图8所示。
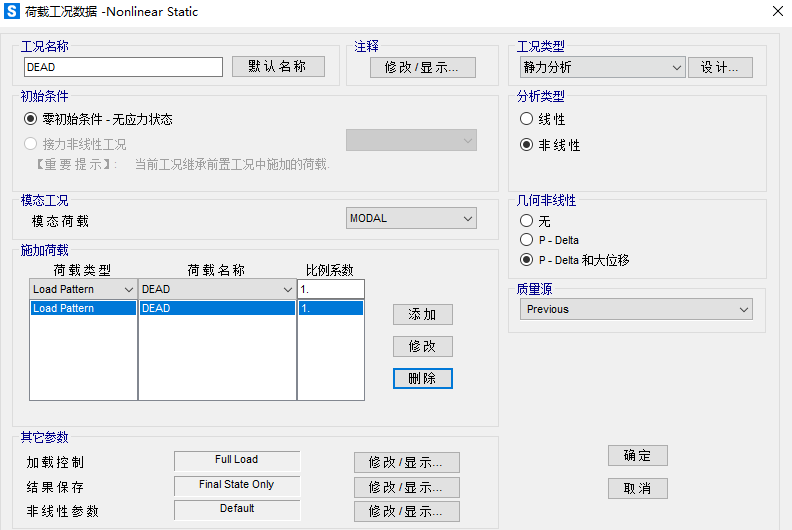
图8 工况设置
2.3 分析迭代
工况设置完成后,运行“DEAD”工况,此时可以得到结构在重力工况下各个节点的竖向位移。依据目标位移法,需要将得到的竖向位移反号施加在节点的坐标上修改节点的坐标。SAP2000中通过命令:分析>修改未变形几何,勾选目标位移法,荷载工况设为“DEAD”,缩放系数设为1。修改完成后再次进行计算,完成第一次迭代,以4号节点为例,可以看到其“%差异”为0.5%,如图9-a所示。第一次迭代完成后,由于其误差较大,按上述方式进行第二次迭代,完成第二次迭代后可以看到4号节点的“%差异”为0.0%,满足要求,迭代完成。
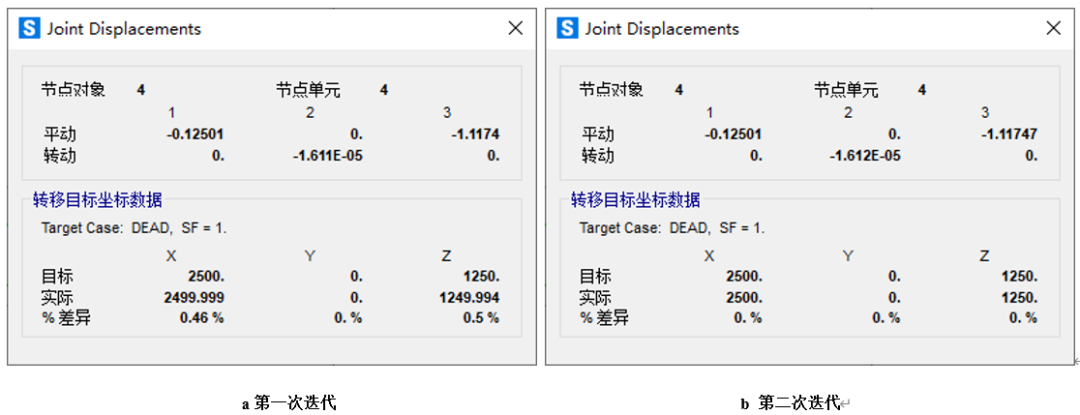
图9 4号节点位移图
为便于解释程序的计算过程,将4号节点坐标和节点位移整理到表1中。其中节点的初始坐标为上一次迭代变形后的坐标,如表1中两块灰色的区域,两组数据是相等的。%差异 =(当前工况计算的位移 - 上一次迭代的位移)/上一次迭代的位移。如1中第一次的迭代后,z方向的%差异,0.5028%=(-1.11740+1.11181)/-1.11181。
表1 4号节点坐标及位移结果
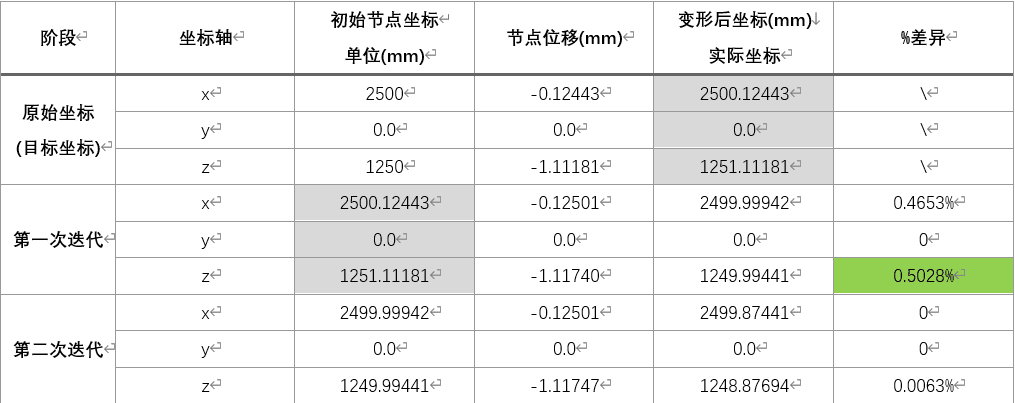
完成第二次迭代后,该索杆结构的轴力分布如图10所示。将该索力提取出来,与论文[2]中的轴力值进行比较,如表2所示。可以看到,两者最大差异不超过0.05%,如果忽略有效数字的差异,SAP2000在考虑该结构自重的条件下计算的索力与论文[2]数值几乎完全吻合。
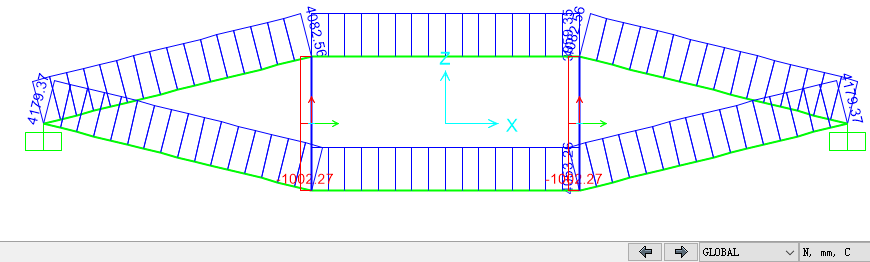
图10 索轴力分布
表2 杆件轴力比较

需要注意的是该索杆结构,当索力与撑杆轴力在各个节点位置处平衡时,结构即可达到平衡态。因此对于不同的初始索张力,是可以找到不同的索力分布的。这里可以通过多次试算来求得所需的索力分布。
3.算例1:穹顶结构
索穹顶结构一般是先设计出结构造型,再求解出实现这种造型所需要的预应力。以肋环型索穹顶为例,要实现其结构造型,各拉索、撑杆之间的预应力比例关系是唯一的。如下图所示,一旦构件的尺寸发生变化,如撑杆变长,建筑造型就不同了,构件之间的预应力比例关系也要发生相应的变化。反之,如果按照一定的尺寸比例关系加工索和撑杆,将他们按照相应的关系连接起来,将斜索和脊索连至固定端,结构就张拉成型了,并且成型后的预应力比例关系是不会变的。
如图11-a所示的Geiger型索穹顶结构,其跨度为100m,设有三道环索。已知结构的几何参数,如图11-b所示。该结构中钢材的密度均为ρ=7850kg/m3,索的弹性模量E=1.7x1011Pa,撑杆的弹性模量E=2.1x1011Pa,结构各个杆件的截面面积如表3所示。在SAP2000中通过支座位移法求解该结构在自重作用下达平衡状态时的预应力分布。
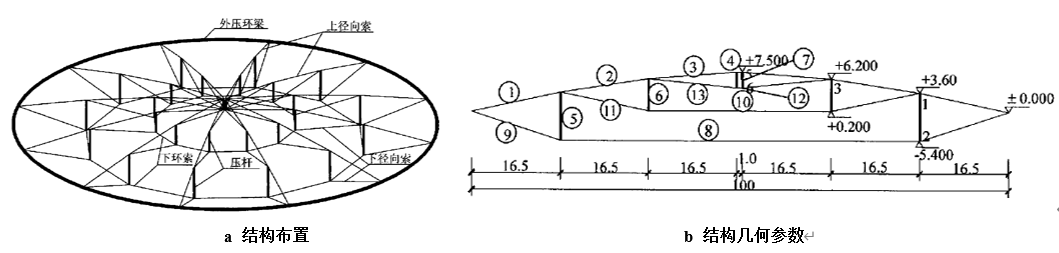
图11 穹顶结构
表3 穹顶结构构件尺寸图
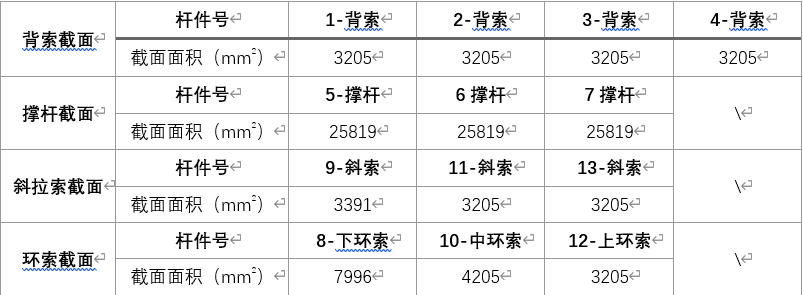
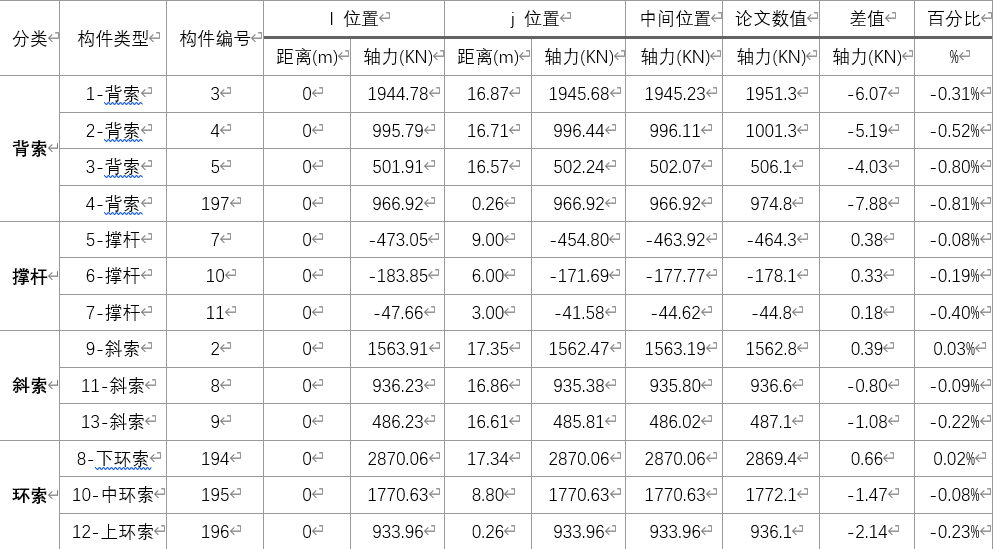
在SAP2000中通过轴网功能快速建立该穹顶结构的模型,该结构外压环梁刚度较大,本模型中并没有建立外压环梁而是将其简化为固定铰接支座处理,如图12-a所示。通过多次迭代后,提取该穹顶单榀结构索杆的轴力分布如图12-b所示。将该索力整理到Excel,与论文[3]中的轴力值进行比较,如表4所示。可以看到,两者最大差异不超过1.0%,SAP2000在考虑该结构自重的条件下计算的索力于论文数值基本吻合。
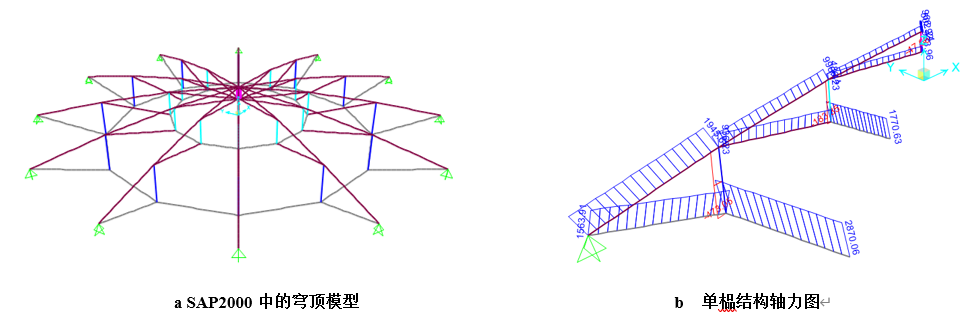
图12 SAP2000穹顶结构模型
表4 穹顶结构杆件轴力比较
4.算例2:环形张力索结构
环形张力索结构由车辐式悬索结构的受力机理演化而来,其构成特点是:结构中部设有大开孔的中心环状结构,外侧有一个刚度较大的受压外环,通过沿径向布置的拉索或索桁架连到中心受拉内环;拉索或索桁架的张拉力与外环的压力平衡,整个结构属于自平衡受力体系。此类结构同样可以通过目标位移法来计算结构的初始预应力分布。
如图13-a所示的为环形张力索桁结构,已知该结构的几何拓扑关系,结构外圈半径为100m,内圈半径为70m。整个结构分为对称的24榀,结构切面视图如13-b所示,其内侧设有两类撑杆,其中长撑杆长度为20m,短撑杆长度为14m。该结构中钢材的密度均为ρ=7850kg/m3,索的弹性模量E=1.7x1011Pa,撑杆的弹性模量E=2.1x1011Pa,结构各个杆件的截面面积如表4所示。在SAP2000中通过支座位移法求解该结构在自重作用下达平衡状态时的预应力分
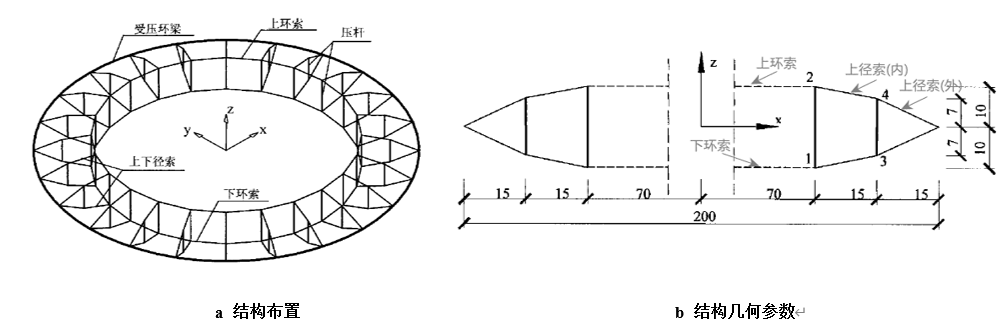
图13 环形张力索结构
表5 环形张力结构杆件尺寸

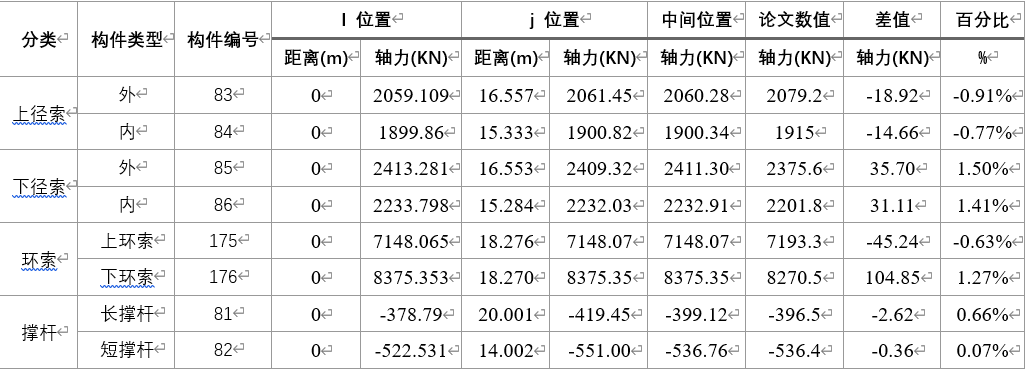
在SAP2000中建立该穹顶结构模型,如图14-a所示。该结构中外侧受压环梁刚度较大,本模型中并没有建立外侧受压环梁,而是将其简化为铰接支座处理。通过多次迭代后,该环形张力结构单榀索杆的轴力分布如图14-b所示。将该索力整理到Excel,与论文[3]中的轴力值进行比较,如表6 所示。可以看到,两者最大差异约为1.5%,SAP2000在考虑该结构自重的条件下计算的索力与论文数值基本吻合。
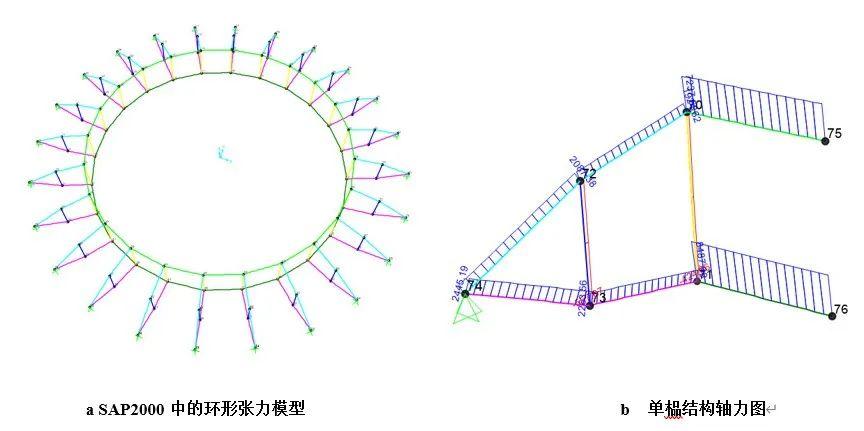
图14 SAP2000穹顶结构模型
表6 环形张力结构杆件轴力统计
5.总结
位形的确定是张力结构设计与分析中最基本也是最为关键的问题。SAP2000中的目标位移法适用于处理第一类找形问题:已知结构的拓扑几何关系求解满足位形要求的索力分布。该方法具有概念明确,操作简单,计算速度快的特点。并通过合理的参数控制,其计算结果可以达到很高的精度。该方法可以作为结构找形分析的一种有力的分析工具。



.png?imageView2/0/w/480/h/270)

