如果40年前的那次地震再次发生,今天的唐山将会怎样? |唐山大地震40周年纪念
40年前的今天,1976年7月28日,唐山被地震顷刻夷为平地。造成24万人死亡,285万间房屋倒塌(楼房每14m2折合1间),96万间房屋严重破坏(图1.1)。 
图1.1 40年前唐山地震后的场景(来源:新华网)
如今40年过去了,如果40年前的那次地震在今天的唐山再次发生,将会怎样?针对这个问题,清华大学土木工程系在唐山市及清华同衡规划设计研究院的支持下,采用课题组开发的城市抗震动力弹塑性分析方法,对当前唐山市中心约23万栋建筑进行了震害模拟,并分析了当前唐山市的建筑抗震设防水平,模拟技术细节参见本文的第三节“相关技术支撑”。
2.1 建筑震害模拟结果
由于唐山地震没有记录到近场主震记录,我们从FEMA(美国联邦应急管理署)P695报告中挑选了4条代表性近场地震记录(中国台湾Chichi记录震级为7.6级,土耳其Kacaeli记录震级为7.5级,美国Denali地震震级为7.9级),其震级和唐山地震(7.8级)相当。并按照胡聿贤等建议的衰减关系,将其输入到每个建筑物,得到每栋建筑物不同时刻不同楼层的震害过程。
唐山市23万栋建筑的震害分布如图2.1、图2.2所示。地震响应动画如视频所示。

(a) 区域震害结果整体视角

(b) 区域震害结果局部视角

(c) 区域地震场景整体视角(t=34.5 s,不同的颜色代表位移的大小)

(d) 区域地震场景局部视角(t=34.5 s)
图2.1 唐山市23万栋建筑震害模拟结果(ChiChi地震动输入)

(a) 区域震害结果整体视角

(b) 区域震害结果局部视角

(c) 区域地震场景整体视角(t = 29.0 s,不同的颜色代表位移的大小)

(d) 区域地震场景局部视角(t = 29.0 s)
图2.2 唐山市23万栋建筑震害模拟结果(Denali地震动输入)

GIF动画1:中国台湾集集地震动下的建筑动态响应

GIF动画2:中国台湾集集地震动下的建筑各楼层破坏情况及分布

GIF动画3:美国Denali地震动下的建筑动态响应

GIF动画4:美国Denali地震动下的建筑各楼层破坏情况及分布
基于上述震害模拟结果,唐山市23万栋建筑在4个地震动下震害分布的情况如图2.3所示。

(a) CHICHI_TCU065地震动(7.6级)

(b) KOCAELI_Yarimca地震动(7.5级)

(c) CHICHI_TCU067地震动(7.6级)

(d) DENALI_PS10317地震动(7.9级)
图2.3 唐山市建筑震害预测结果
具体而言,不同地震动下建筑不同破坏程度的比例及汇总结果如表2.1所示。
表2.1 不同地震动下建筑不同破坏程度的比例(面积比)
地震动 | 结构类型 | 完好或 轻微破坏 | 中等 破坏 | 严重 破坏 | 损坏 |
CHICHI TCU065 | 设防结构 | 0.0% | 35.2% | 64.8% | 0.0% |
非设防结构 | 0.0% | 0.3% | 8.7% | 91.0% | |
汇总 | 0.0% | 28.4% | 53.8% | 17.7% | |
KOCAELI Yarimca | 设防结构 | 0.0% | 22.8% | 75.8% | 1.5% |
非设防结构 | 0.0% | 0.0% | 3.0% | 97.0% | |
汇总 | 0.0% | 18.4% | 61.7% | 20.0% | |
CHICHI TCU067 | 设防结构 | 0.0% | 6.9% | 80.2% | 12.9% |
非设防结构 | 0.0% | 0.0% | 5.2% | 94.8% | |
汇总 | 0.0% | 5.6% | 65.7% | 28.7% | |
DENALI PS10317 | 设防结构 | 0.0% | 0.4% | 58.2% | 41.4% |
非设防结构 | 0.0% | 0.0% | 2.6% | 97.4% | |
汇总 | 0.0% | 0.3% | 47.4% | 52.3% | |
平均值 | 设防结构 | 0.0% | 16.3% | 69.7% | 14.0% |
非设防结构 | 0.0% | 0.1% | 4.9% | 95.0% | |
汇总 | 0.0% | 13.2% | 57.2% | 29.7% |
由表2.1可知,在PGA(地面峰值加速度)相同的情况下,由于CHICHI_TCU067和DENALI_PS10317的反应谱强度显著强于其他两个地震动(详见图3.6),因此其破坏比例也明显要高一些。
2.2 次生火灾模拟结果
此外,唐山地震发生后紧接着就下雨,因此没有发生严重的次生火灾。而1906年美国旧金山大地震、1923年日本东京关东大地震、2011年日本311大地震都曾引发严重的次生火灾,因此本研究团队在震害模拟基础上,对地震次生火灾也进行了模拟。采用回归模型计算得到初始起火建筑数量约为544栋,随机选定初始起火位置,进行5次模拟,得到结果如图2.4所示:在不考虑消防救援的条件下,总起火面积约3.1~3.4km2,占建筑总占地面积的9%~10%。

图2.4 起火建筑占地面积随时间的变化曲线

图2.5 地震次生火灾模拟的结果

GIF动画5:次生火灾蔓延动画(全局视角,西风,6m/s)

GIF动画6:次生火灾蔓延动画(局部视角,西风,6m/s)
2.3 分析与讨论
通过对模拟结果的分析发现:
(1)唐山市建筑抗震能力显著提高,设防建筑抗震能力显著优于非设防建筑
根据苏幼坡等统计的唐山大地震的实际震害结果(图2.6),所研究区域在1976年唐山大地震时倒塌率超过80%。模拟结果(表2.1)显示4条地震动下所有建筑的平均倒塌比例为29.76%,因此目前唐山市建筑的抗震能力比1976年超过80%的倒塌比例已经有显著提高。这29.76%的倒塌比例很大程度上是由于大量的老旧未设防建筑导致的。进行过抗震设防的建筑,其平均倒塌比例13.95%,而未设防的建筑,平均倒塌比例达到了95.03%。所以,建筑抗震设防对提高其抗震性能具有决定性的作用。今后应对未设防建筑尽快逐步更新或加固,以解决城市抗震防灾能力的短板。

图2.6 唐山地震灾区房屋建筑倒塌分布图(来源:苏幼坡等)
(2)震后城市重建成本极高,提高城市的抗震“韧性” (Resilience)极为重要
即便是对于设防结构,超过中等破坏的建筑物比例也达到了83.67%,这些建筑基本都不存在修复的价值或可能性。因此,如果1976年唐山地震再次发生,虽然人员伤亡率会得到有效控制,但是基本上整个城市都要重新建设,粗略估算重建面积超过一亿平方米,其经济代价及环境、资源代价都非常高昂。类似问题在国外已有众多先例,如2011年新西兰基 督城发生6.3级地震,虽然基 督城的高层建筑无一倒塌,但是因损伤严重没有修复价值,大半被迫拆除重建,造成重大经济损失和社会影响。所以,提高城市的抗震“韧性” (Resilience)极为重要。
重要说明:未来地震发生具有很大的不确定性,特别是对于唐山这样近代发生过大地震的城市,未来地震肯定不会和1976年的地震一模一样。因此,上述分析是基于1976年地震的情景模拟,其宏观统计分析结果对城市抗震防灾具有参考价值,但一般不适用于某个具体单体建筑的抗震评价及震害预测。
3.1 建筑数据
此次分析的对象为唐山市区,清华同衡规划设计研究院提供了唐山市230,683栋建筑的必要信息,包括结构类型、建造年代、层数等。按照建筑面积统计,不同年代的建筑分布如图3.1所示,不同结构类型的房屋分布如图3.2所示。

图3.1 建筑年代比例(按照建筑面积统计)

图3.2 建筑类型比例(按照建筑面积统计)
3.2 分析模型
基于课题组提出的城市抗震动力弹塑性分析方法,采用多自由度剪切层模型和多自由度弯剪层模型对建筑物建模(图3.3),相关模型介绍参见:

图3.3 多自由度剪切层模型和多自由度弯剪层模型
[1] Parameter determination and damage assessment for THA-based regional seismic damage prediction of multi-story buildings, Journal of Earthquake Engineering, 2016. DOI: 10.1080/13632469.2016.1160009.
[2] A nonlinear computational model for regional seismic simulation of tall buildings, Bulletin of Earthquake Engineering, 2016, 14(4): 1047-1069.
3.3 地震动输入
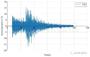
由于唐山地震发生时,我国强震观测站很少,因此主震在8度以上区未测得强震记录,较好的主震记录为北京饭店测得的地震记录,但此处烈度为6区,距离震中157km。考虑到北京饭店测得的地震动经历了较远距离的传播,已经不能很好的表征极震区的地震动特征,因此本次模拟从FEMA(美国联邦应急管理署)P695报告中挑选了4条代表性近场地震(震源距小于10 km)记录,它们分别是中国台湾Chichi记录震级为7.6级,土耳其Kacaeli记录震级为7.5级,美国Denali地震震级为7.9级。其震级与唐山大地震相近,各地震动未调幅时程曲线如图3.4所示。 
(a) CHICHI_TCU065

(b) KOCAEL_Yarimca

(c) CHICHI_TCU067

(d) DENALI_PS10317
图3.4 四条近场地震动未调幅时程曲线
由于目标区域范围较广,单一的地震动输入和实际情况相差较大,此次模拟采用胡聿贤等提出的地震动PGA衰减关系,按照唐山大地震的震级和各个建筑距离震中的距离,得到如图3.5所示的地震动PGA的分布图,以此作为各个建筑地震动的输入参数。按照图3.5的衰减关系,将四条近场地震动调幅后得到震中附近的地震动反应谱,如图3.6所示。可见震中附近地震动反应谱显著高于我国抗震规范规定的9度罕遇地震反应谱。

图3.5 采用胡聿贤等建议的衰减关系得到的地震动PGA分布图(单位:cm/s2)

(a) CHICHI_TCU065

(b) KOCAEL_Yarimca

(c) CHICHI_TCU067

(d) DENALI_PS10317

(e) 反应谱对比
图3.6 调幅后震中附近的地震动时程曲线和反应谱曲线
3.4 地震次生火灾模拟
课题组基于任爱珠教授、赵思健等的工作,编写了地震次生火灾模拟程序。程序采用回归模型计算起火建筑数量,采用火灾蔓延物理模型模拟火灾蔓延的两个重要因素,即热辐射、热羽流,考虑了风向、风速、结构类型、震害程度等的影响。主要参考文献如下:
[1] The simulation of post-earthquake fire-prone area based on GIS. Journal of Fire Sciences, 2004, 22: 421-439.
[2] GisFFE-an integrated software system for the dynamic simulation of fires following an earthquake based on GIS. Fire Safety Journal, 2010, 5(2): 83-97.
[3] A Physically-based model for urban fire spread. First Safety Science-Proc. Seven International Symp.. 2002, 129-140.
3.5 不同地震动衰减关系的影响
此外,考虑到地震动衰减关系的不确定性,我们在中国地震局俞言祥研究员等的支持下,采用第五代区划图推荐的衰减关系,生成了唐山地震PGA分布如图3.7所示。采用该衰减关系及图3.2的四条地震动记录,也可以得到相应的震害预测结果,总体规律和表3.1基本一致,只是由于第五代区划图推荐的衰减关系计算得到的PGA(图3.7)更大,因此震害更严重一些,如表3.1所示。如果将图3.7和图3.5相结合,将震中附近PGA根据图3.5降低到0.85g左右,则震害又会小一些(表3.1)。
 图3.7 按第五代区划图得到的PGA分布(感谢中国地震局支持)
图3.7 按第五代区划图得到的PGA分布(感谢中国地震局支持)
表3.1 按照第五代区划图衰减关系得到不同破坏程度的比例(面积比)
震中附近PGA | 结构类型 | 完好 | 轻微破坏 | 中等破坏 | 严重破坏 | 损坏 |
1.16g | 设防结构 | 0.0% | 0.0% | 5.5% | 76.0% | 18.6% |
非设防 | 0.0% | 0.0% | 0.0% | 2.5% | 97.5% | |
汇总 | 0.0% | 0.0% | 4.4% | 61.8% | 33.8% | |
0.85g | 设防结构 | 0.0% | 2.5% | 28.3% | 58.6% | 10.5% |
非设防 | 0.0% | 0.0% | 0.6% | 8.1% | 91.3% | |
汇总 | 0.0% | 2.1% | 23.0% | 48.8% | 26.2% |
当然,从区域震害模拟的角度上说,最合适的情况,应该是类似鲁甸地震龙头山镇震害模拟那样输入真实的地震动记录(见以往的分析案例:龙头山镇模拟),或者类似CBD震害模拟那样输入根据震源和传播机制生成的宽频带地震动时程输入(见以往的分析案例:CBD模拟)。在本次分析中,由于未得到类似的地震动输入,所以采用了一些比较近似的方法。如果可以得到更加真实的唐山地震动模拟数据,则可以进一步提高震害模拟的可靠性。
课题组在城市抗震动力弹塑性分析方面已经积累了比较便捷的方法。因此,本次唐山震害模拟主要由本科生程庆乐等完成,从拿到初步数据到完成上述分析用时不足2个月(大部分时间用在数据的检查、核对和完善上)。与此同时,由于城市抗震动力弹塑性分析还是一个新生事物,我们的工作一定有很多缺点和不足,也请同行批评指正。希望与国内外同行共同合作,为提高我国城市的抗震水平而努力。
参与本次分析的除程庆乐、曾翔外,还有许镇、杨哲飚等。
1:2014年光华论坛PPT: 基于GPU高性能计算的城市地震灾害预测与可视化
2:论文:城市区域高层建筑的地震响应模拟方法
3:论文:用于区域震害模拟的多自由度剪切层模型参数确定方法
4:陈肇元院士8年前提出的问题:如果重遇1679年康熙年间8级三河-平谷特大地震会成为什么样子?
5:论文:建立GPU集群,轻松实现城市地震弹塑性时程分析
6:论文:如何减轻建筑外围护结构脱落地震次生灾害?
7:论文:下一代性能化设计方法在区域地震经济损失预测中的应用