NFX|非线性动力(显示)分析
线性动态分析概述




基于材料而言,计算线性和非线性差异:
使用线性,相对昂贵,解决可逆的变形和位移小
使用非线性,相对经济,解决永久变形和/或大的位移
非线性包含

[M]{a} + [C]{v} + [K]{x} = {F}



运动方程是解决方案
-问题是用有限元的方法对方程进行描述
-用数值方法得到的解决方案
-数值解的性质是把加在一起增量结果
-通过穿越时间域在增量步骤中求解而得到结果
-隐式和显式方法的增量计算的结果彼此不同
Sum( [M]{a}+ [C]{v} + [K]{x} = {F} @ incrementaltime steps)
隐式积分专注于位移刚度矩阵的逆
{x}= [K]-1 ({F} and other components here)
–刚度矩阵的逆是一项艰巨的任务
–平均加速度和位移计算在时间步
显式积分专注于加速质量矩阵的逆
{a}= [M]-1 ({F} and other components here)
–通常情况下,质量集中和质量矩阵成为对角矩阵.
–对角矩阵求逆容易

在中心差分法中,速度和加速度可以用位移表示为:




(2)中心差分法是条件稳定算法。当求解具体问题时,时间步长Δ𝑡必须小于临界值 Δ𝑡𝑐𝑟,否则算法是不稳定的。

上式中𝑇𝑛是有限元系统的最小固有振动周期,理论上,系统的最小固有振动周期总是大于或者等于最小尺寸单元的最小固有振动周期,因此,网格中最小尺寸的单元决定中心差分法时间步长的选择。


临界时间步长由材料特性
弹性模量、泊松比、密度和单元特征长度决定
单元特征长度越短,弹性模量越大,临界时间步长越小,分析时间越长

midas NFX 支持非线性(隐式、显式)动力分析
-支持六面体、四面体、金字塔等多种单元,能够方便而准确地分析
-非线性材料:弹塑性模型,超弹性模型(Mooney-Rivlin,Ogden, Blatz-Ko 等)
-非线性几何:大变形,大转动,大应变,随从力
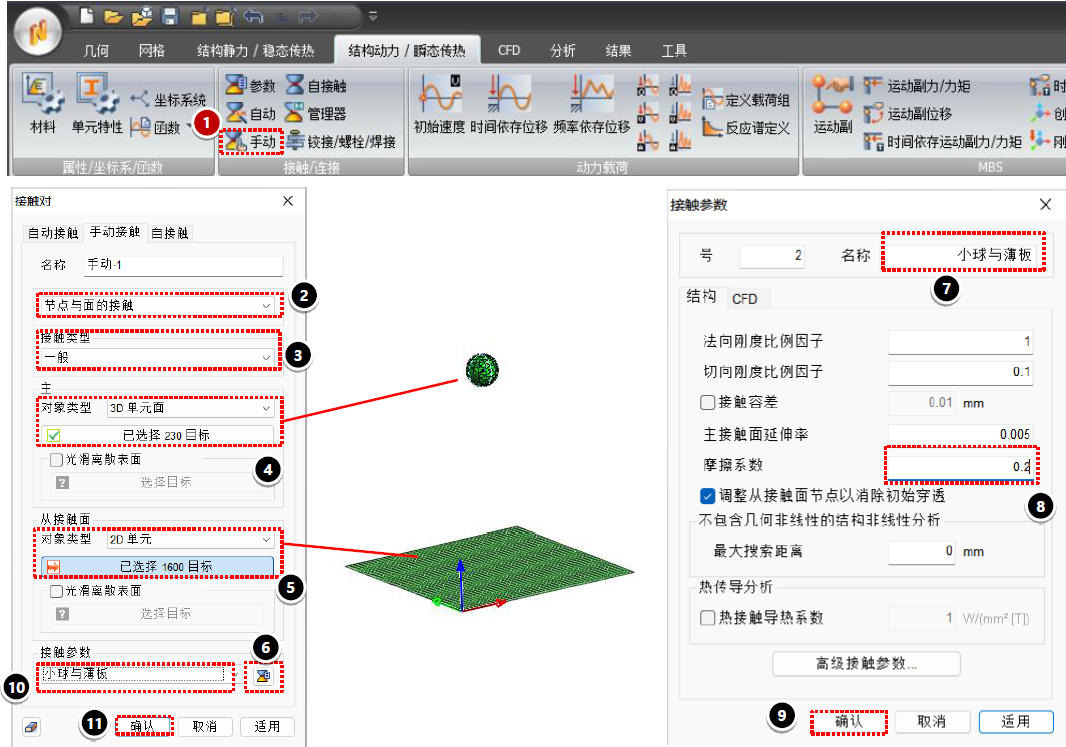
-非线性接触:面和面接触/自接触,粗糙/一般接触(摩擦)
-自动计算质量缩放/阻尼,以及临界时间步长




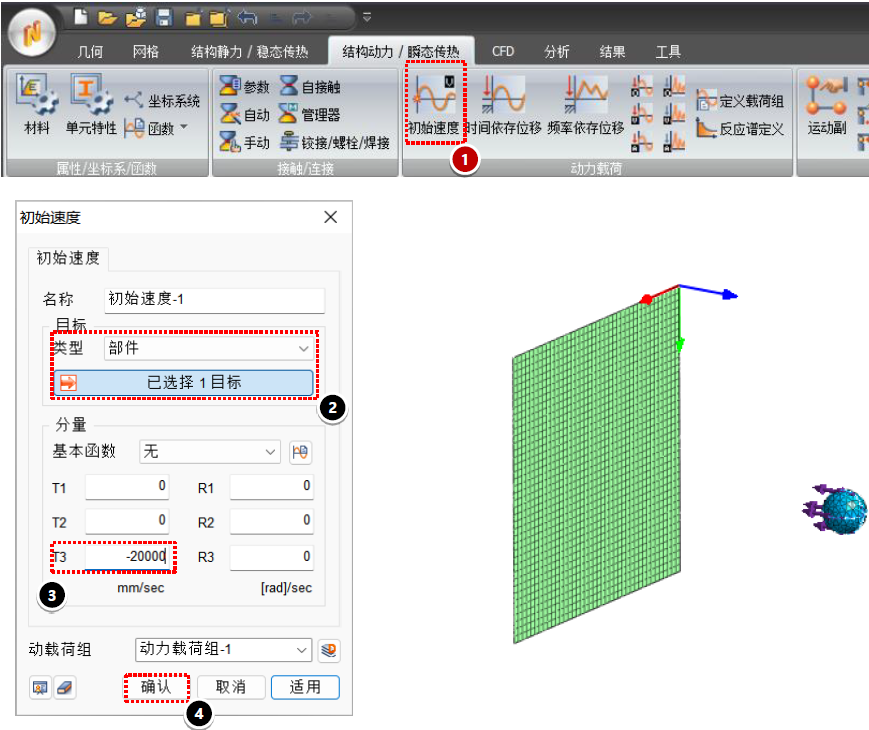
侵彻分析











相关文章,在仿真秀官网搜索:
断裂分析(Explicit Broken)
跌落分析应用案例讲解




