NFX|非线性隐式动力
midas NFX 使用 Hilber 、Hughes 和 Taylor 提出的方法 (HHT-α) 进行隐式直接时间积分。HHT-α方法是Newmark方法的广义形式,并保留了可控的数值阻尼效应。因此,它可以控制高频噪声并保持与Newmark方法相同的时间步长的二阶精度。HHT-α方法使用如下修改形式的动态平衡方程:
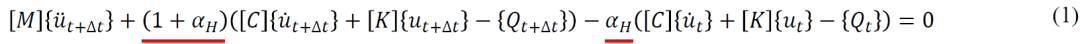
 的取值范围是
的取值范围是 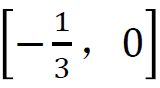 ,决定数值阻尼效应。
,决定数值阻尼效应。引入下列假设
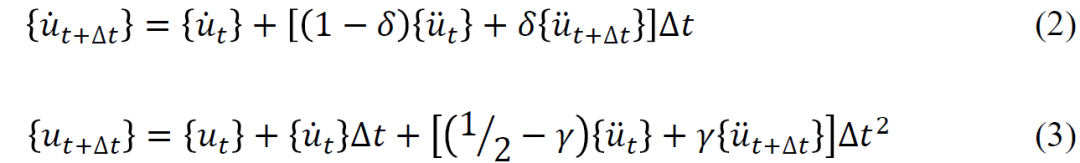 用(2)式和(3)式重新构建(1)式的动力学方程,得到:
用(2)式和(3)式重新构建(1)式的动力学方程,得到: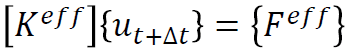
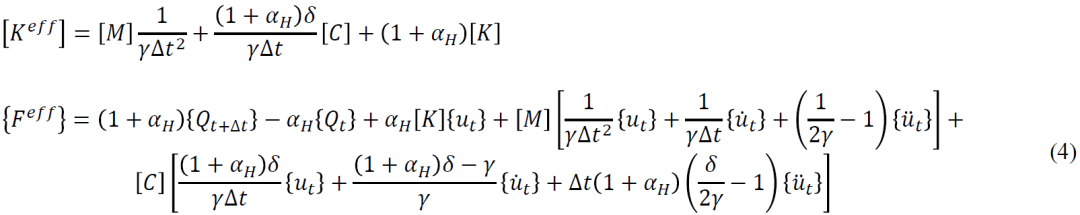
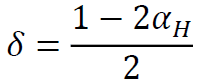 时,HHT-α积分是无条件稳定的;当
时,HHT-α积分是无条件稳定的;当  =0,变成平均加速度法的 Newmark方法。
=0,变成平均加速度法的 Newmark方法。 默认取值为 -0.05
默认取值为 -0.05Newmark方法 (  =𝟎)
=𝟎)

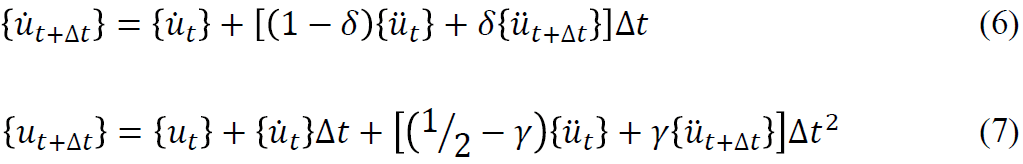
用(6)式和(7)式重新构建(4)式的动力学方程,得到:
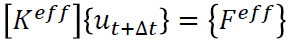


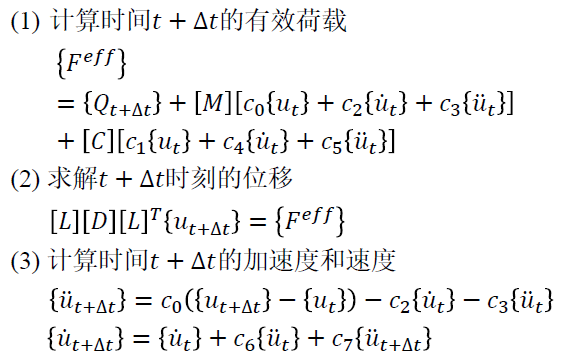
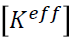 中包含了
中包含了 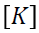 ,而一般情况下,
,而一般情况下, 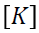 是非对角矩阵,所以在求解
是非对角矩阵,所以在求解 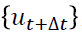 ,
, 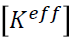 的求逆是必须的。这种算法称为隐式算法。
的求逆是必须的。这种算法称为隐式算法。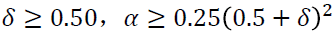 ,Newmark方法是无条件稳定的,即时间步长Δt的大小可不影响解的稳定性。此时,Δt的选择主要根据解的精度确定,具体说可对根据对结构响应有主要贡献的若干基本振型周期的最小者
,Newmark方法是无条件稳定的,即时间步长Δt的大小可不影响解的稳定性。此时,Δt的选择主要根据解的精度确定,具体说可对根据对结构响应有主要贡献的若干基本振型周期的最小者 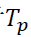 来确定,一般来说,
来确定,一般来说, 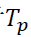 比结构系统的最小振动周期
比结构系统的最小振动周期 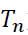 大得多,所以无条件稳定的隐式算法以
大得多,所以无条件稳定的隐式算法以 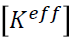 的求逆为代价换取比有条件稳定显式算法大得多时间步长Δt。
的求逆为代价换取比有条件稳定显式算法大得多时间步长Δt。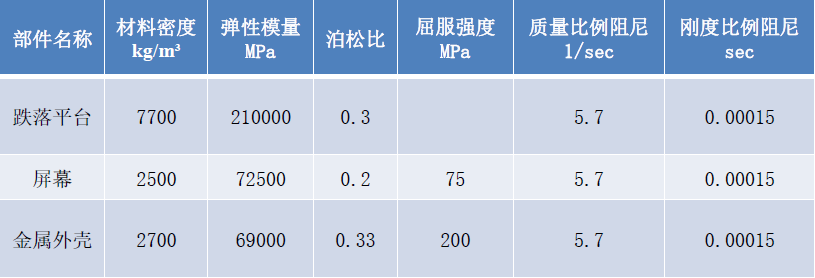
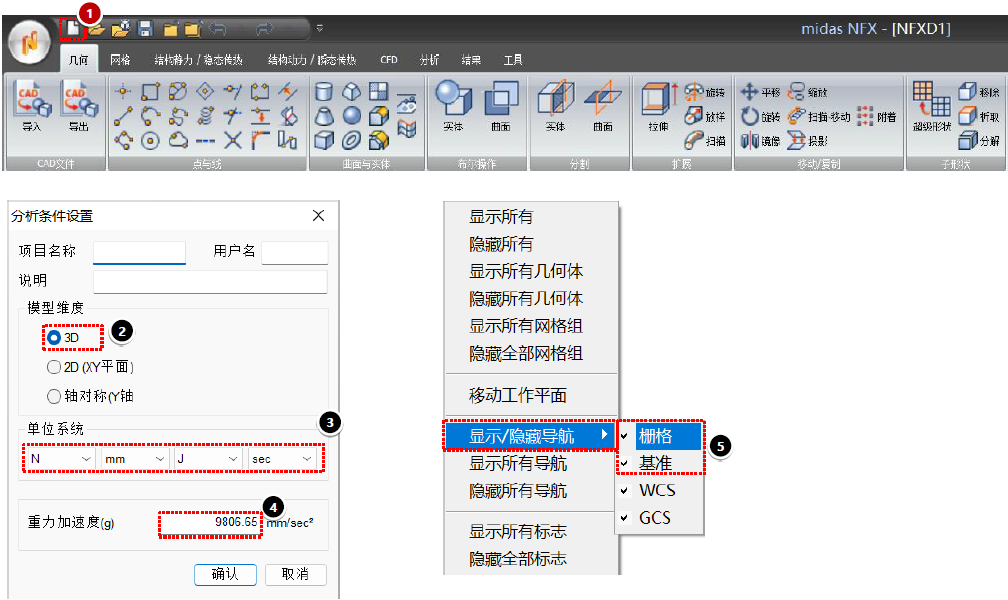
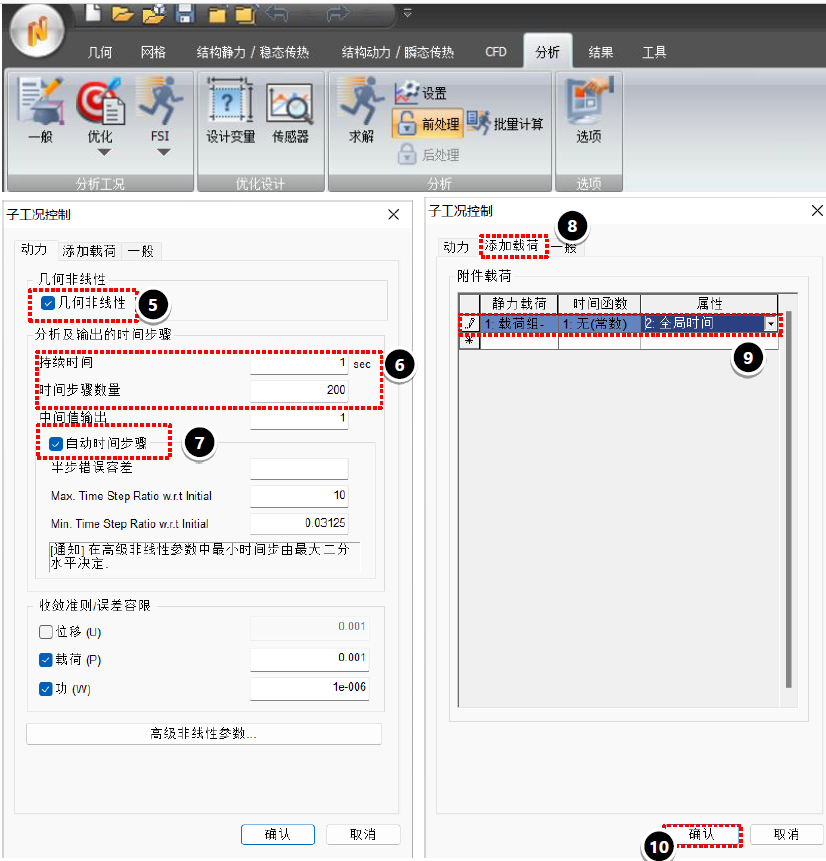
开始模拟前:环境条件设置
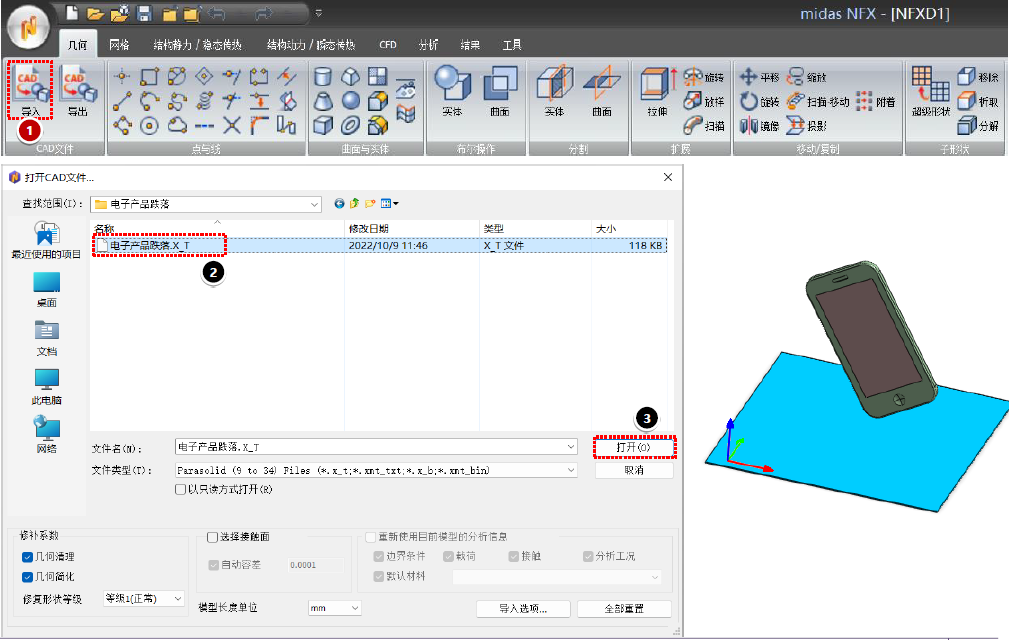
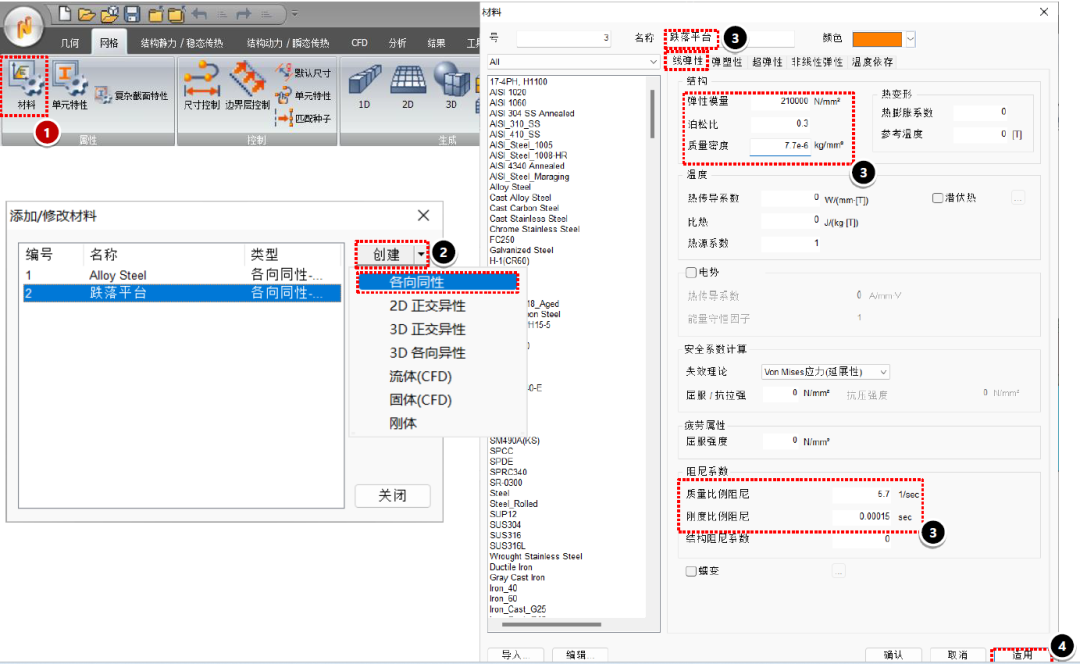
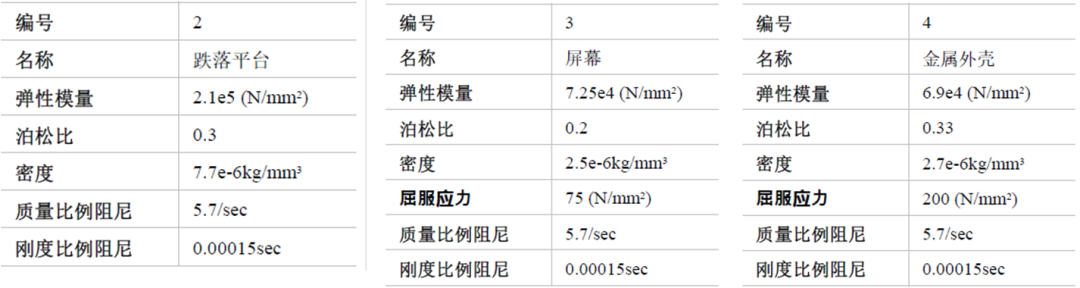
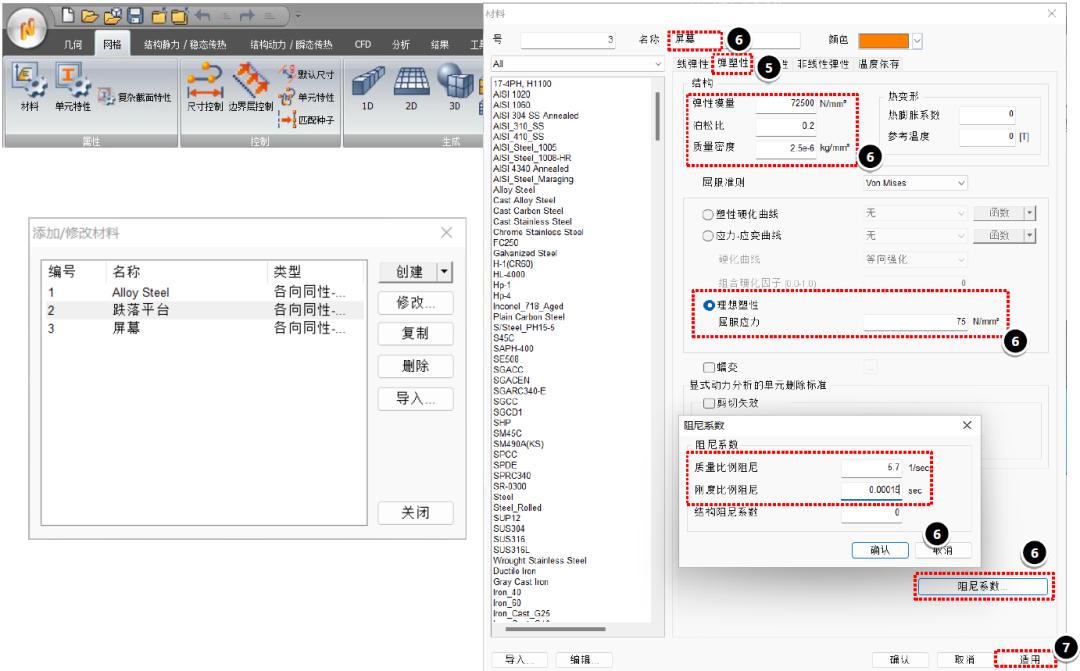
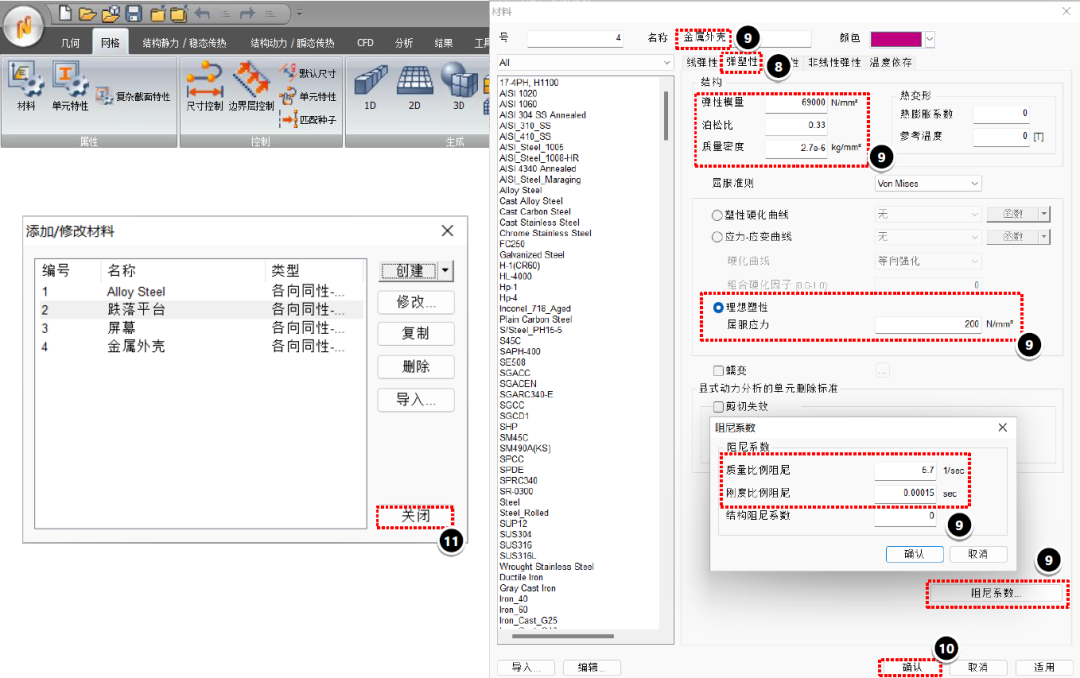

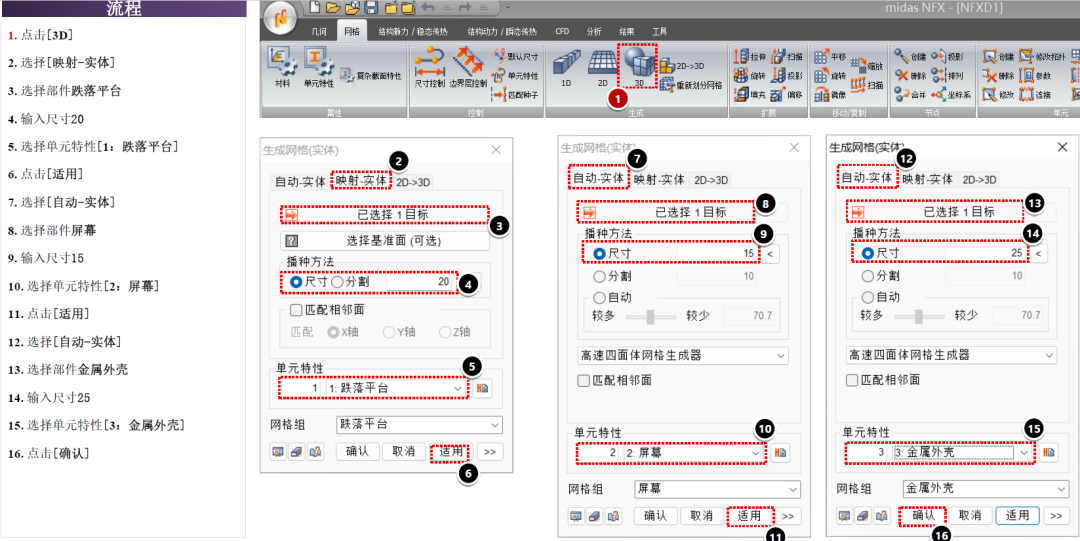

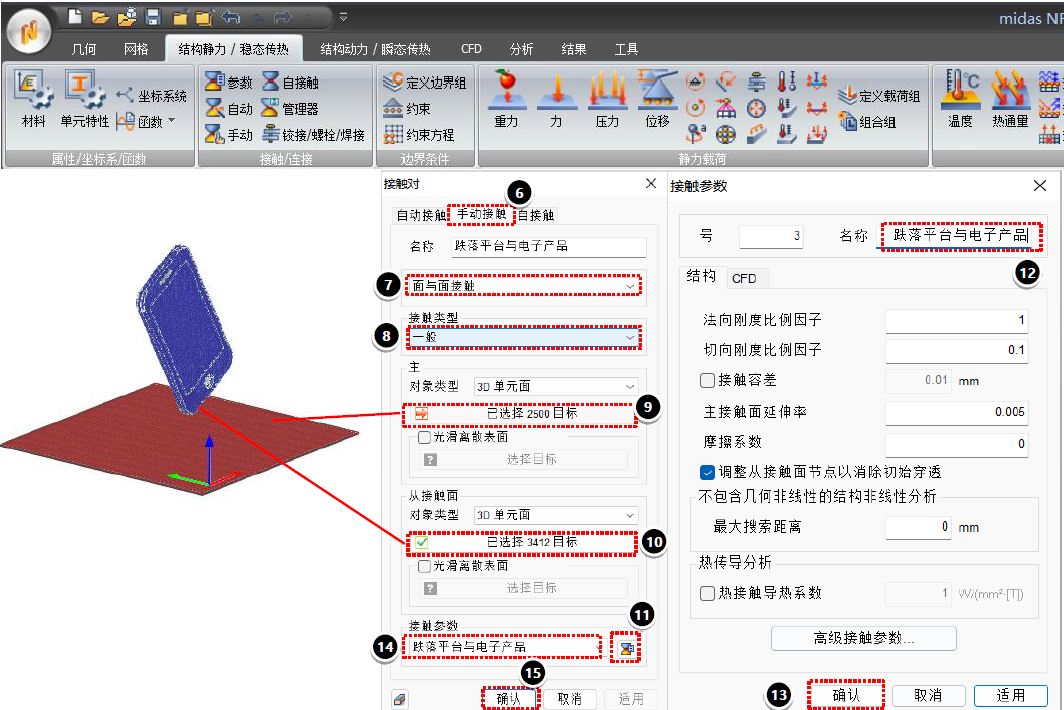

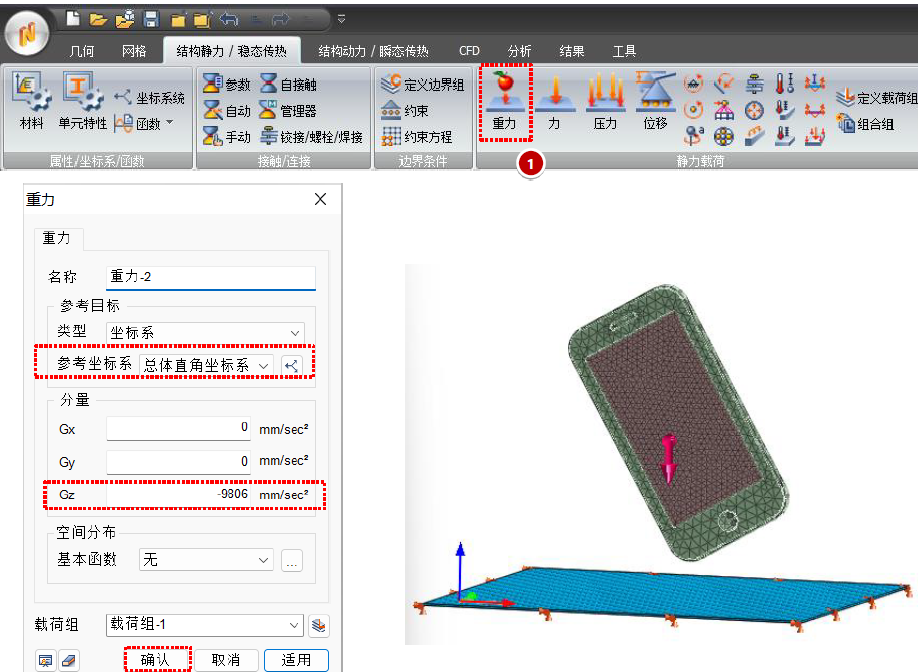
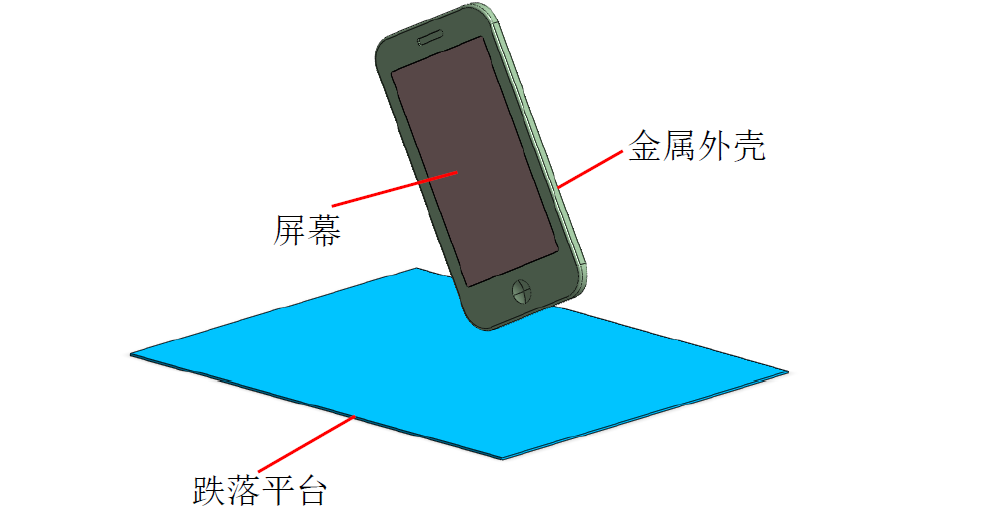
屏幕和金属外壳两个部件施加初始速度


登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-03-22
最近编辑:1年前
还没有评论
相关推荐
最新文章
热门文章




