用简化有限元法降低传动系统噪声
2017-26-0215 Driveline Boom Noise Reductionthrough Simplified FEMKodali Ajay Krishna and Sanjeev
PatilMahindra & Mahindra, Ltd. 在当今竞争激烈的汽车市场上,随着汽车开发时间的缩短和原型/测试的减少,CAE技术在汽车开发中发挥着至关重要的作用。汽车环境要求不断提高汽车的精细化水平。性能和精细化是影响汽车市场接受度的关键因素动力传动系统是提高客户满意度的关键系统之一,其优化对提高客户满意度起着至关重要的作用。由于传动系统的功能性,传动系统引起的噪声和振动是全轮驱动车辆开发计划中最常见的问题传动系的优化需要复杂的非线性整车CAE-MDB模型来评估不同工况下传动系的噪声和振动响应[1]。本文采用一种简化的方法来解决在AWD车辆开发的原型测试水平上识别出的噪声和振动问题。以线性有限元法为基本工具,分析其根本原因,提出设计方案。在所提出的工作中,建立了全柔性FE传动系统的模态分析模型,并将ODS与试验行为相匹配。在建立了有限元与试验的相关性后,对不同的系统变量进行了优化,以降低系统级响应随后,对这些解决方案的座椅振动和座舱噪声水平进行了评估。该技术可以在时间、资源和系统内部细节不可用或有限的情况下用于建立完整的非线性CAE模型通过这种简化的方法,有可能快速解决由传动系引起的N&V问题。在高速多缸柴油机中,噪声和振动一直是最关键的问题。传统上,全轮驱动车辆具有纵向动力系统配置,最近对紧凑型横向动力系统车辆的需求有所增加除此之外,人们对更省油的车辆和更高的驾驶性能也有着强烈的需求,这导致了由于高“低端”扭矩要求而带来的NVH方面的挑战增加这将有增加传动系扭振的趋势利用计算机辅助工程(CAE)技术,如有限元方法,作为预测NVH性能的工具,已成为汽车工业解决传动系NVH问题的标准方法。为了使用分析工具评估动力传动系统的振动状况,有必要简化或“理想化”动力传动系统的子系统然而,传动系的扭转弹性系统是弹性元件和质量的复杂组合。典型的轴系统是在相当长的长度上分布质量,而齿轮、离合器和飞轮集中在传动系统的一个位置。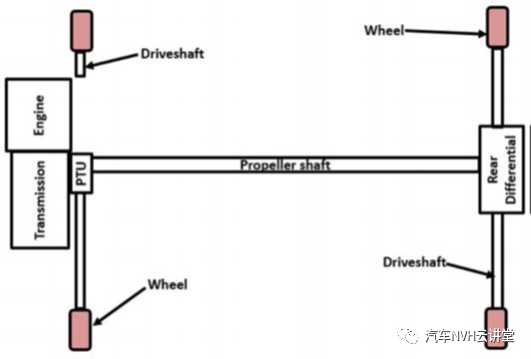
解决传动系统问题的传统方法是通过具有等效惯性和扭转刚度的圆盘和轴等高度简化单元来表示复杂的传动系统部件,并求解系统参数但是,即使使用先进的技术和工具,识别传动系系统不同元件的刚度值、惯量和适当的阻尼值也是一个耗时的过程本文提出的方法是唯一的,它使用简化的线性有限元模型。如图1所示,全轮驱动部件(如PTU、传动轴、后差速器和后驱动轴)将转动惯量添加到前驱动系统中,从而使固有频率接近发动机较高的扭振激励范围动力传动系动臂的进一步噪音是动力传动系振动和车身响应之间相互作用的结果AWD系统将创建到车身系统的附加加载路径如果存在传动系吊杆,驾驶员可能会遇到不可接受的噪声和/或振动(2),这可能是由于传动系激励或车身传动系对车身激励的敏感性增加所致。这就为我们提供了一个很好的机会来了解其根本原因,解决NVH问题,并在未来的项目中避免它。与传动系统相关的NVH问题在本质上是复杂的,并且随着激励的变化而呈现。在不同的工作条件下,需要一个非线性多体仿真工具(MDB)来评估多个轴承座位置的力传动系MDB模型需要使用适当的复杂接头(如U形接头和Cv接头)构建完整的复杂整车模型[2]。传动系统模型的输入是由于燃烧压力引起的活塞和曲柄运动产生的驱动扭矩。这需要大量的数据和建模将需要大量的时间。典型的MD模型将主体视为刚性系统,然后将一个或多个系统转换为柔性系统。在MD模拟中,将整个传动系转换为柔性是非常困难的。具有灵活系统的典型的MD,解决时间将是巨大的,它需要高端硬件配置。本文所发展的方法/过程采用线性有限元分析,以简化的方式解决复杂的传动系问题。本文所采用的简化分析模型涵盖了传动系的大部分物理特性,可以作为解决NVH传动系现场问题的快速模型。
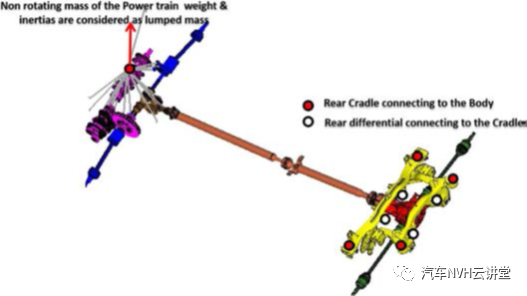
研究中的车辆是一个单体车身,全轮驱动配置,由4缸柴油发动机和6速变速器横向安装传统的全轮驱动部件,如ptu、传动轴、后差速器和传动轴系统都出现在车内。如图2所示后差速器使用四个衬套安装在托架上,后托架通过另外四个衬套连接到车身。在所研究的给定车辆中,噪声和振动问题在程序的原型测试级别被识别在发动机转速1500至1800转/分的范围内,发现中后乘客位置的噪音和振动很大在相同发动机转速范围内的所有档位条件下都观察到这种行为。阶次分析有助于理解二阶是影响整体噪声和振动特性的主要因素。在57Hz时,发动机1710 RPM的主要二阶部件产生了更高的振动和噪音。在对前排和最后一排乘客位置敏感的50HZ附近也观察到声腔模态,导致噪声和振动放大。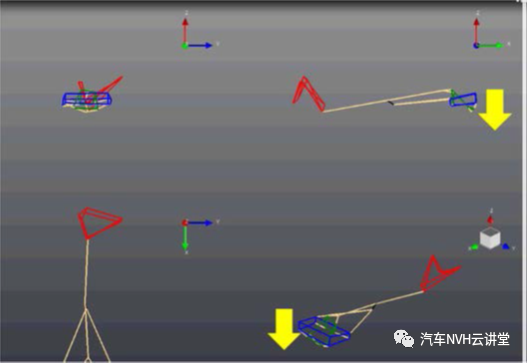
图3(b). ODS @57Hz-高位
图3显示了传动系统在问题频率范围内的运行偏差形状(ODS)图3(a)和3(b)显示了57Hz的极端位置从ods中观察到后副车架(蓝色)和后差速器(绿色)在异相运动中垂向跳动,线性有限元法可作为识别根本原因和提出设计方案的基本工具。本文提出的方法可以快速解决全轮驱动系统的问题图4说明了使用基本线性模型来解决传动系统问题的整个过程。由上白车身、封闭件、座椅和相关装饰件组成的完整装饰车身(TB车身)被建模为有限元系统,并针对相关传递函数进行组装和求解对完整的柔性传动系统进行模态分析,提取临界模态。然后在适当的加载条件下对传动系统进行激励,以模拟试验条件进一步快速提取不同的传动系统响应解,通过改变设计变量来降低系统级响应随后,检查这些解决方案的车身振动和噪声对动力传动系统激励的敏感性。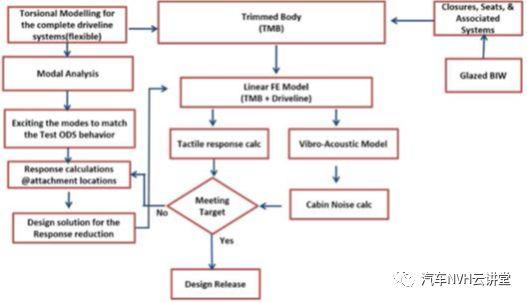
如前所述,MDB模拟需要完整的系统惯性和刚度信息,但在研究系统的情况下,后差速器的内部细节(惯性等)不可用这些细节在NASTRAN中近似,随后使用有限元模型来模拟传动系。进一步使用Rigids和MPC对适当的接头进行建模,并进行模态分析使用模态数据作为传动系统的自由度,在齿轮箱输入轴的已知激励下(如图5(a)所示)进行扭转响应研究如图5(b)所示,计算了副车架位置所有附件的加速度响应。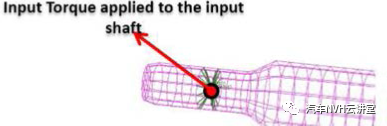

虽然在副车架连接位置的响应最大值是54赫兹,这接近于有问题的测试频率,但模拟的ODS并不代表测试ODS。由于模拟中的扭振激励不存在系统不平衡,因此动力传动系统的响应导致了副车架和差速器总成的俯仰运动,而测试中的ODS显示了副车架和差速器总成的异相弹跳运动因此,为了表示57Hz的测试行为,如图7所示,在后差速器处施加垂直激励,并提取与如图8所示的测试识别行为紧密匹配的响应,这种平面内的垂直激励代表了由此产生的不平衡、旋转轴之间的不对中、传统上在这种动力系统配置中发现的振动产生机制。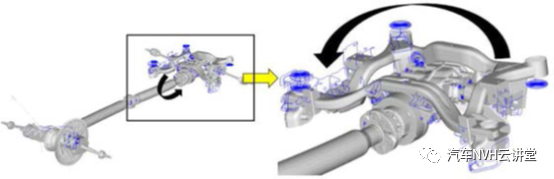
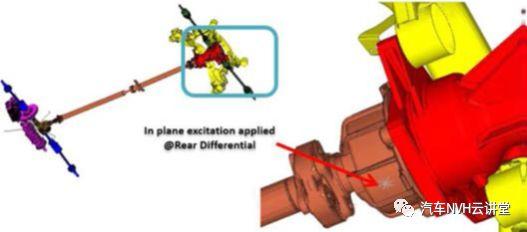
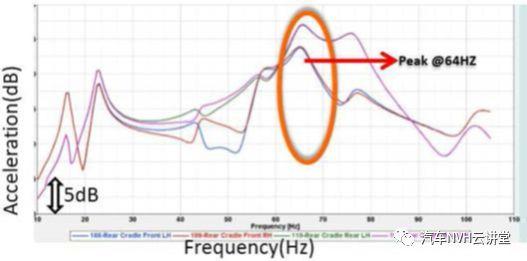
图8显示了为垂直激励计算的响应它观察到最大响应是在64赫兹,接近测试结果的85%,即57赫兹。图9显示了用于垂直面内激励的传动系和副车架总成后部的ODS从ODS可以清楚地看到,后副车架与后差速器弹回不一致。一旦在试验和模拟之间建立了这种相关性,就可以进行不同的设计灵敏度研究,如后面章节所述。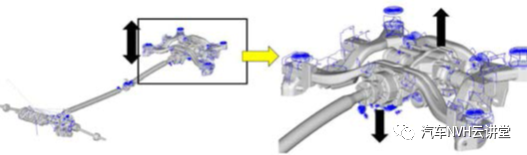
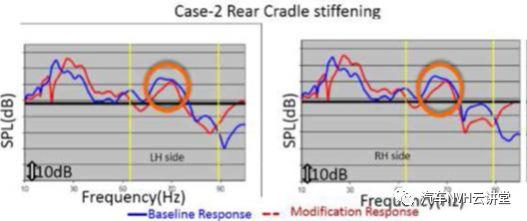
当相关模型在57hz频率的副车架附着点处响应较高时,计算出了减小该响应的解的数目。如图10所示,以下是为降低副车架附着响应而研究的不同情况图11显示了每个案例的结果在案例1中观察到,随着差速器衬套刚度的增加,响应也在增加,这将对振动产生负面影响。然而,在案例2中,副车架衬套刚度增加,反应得到了很好的改善在案例3中,传统的TMD被用于降低响应,在系统级的主频带中可以看到2dB的改善。在副车架附着点处的进一步响应被用作对车身的激励,并且在客户接触点处的响应被从TB车身的模态模型中提取出来,以得到更好的NVH解决方案,这将在后续章节中解释。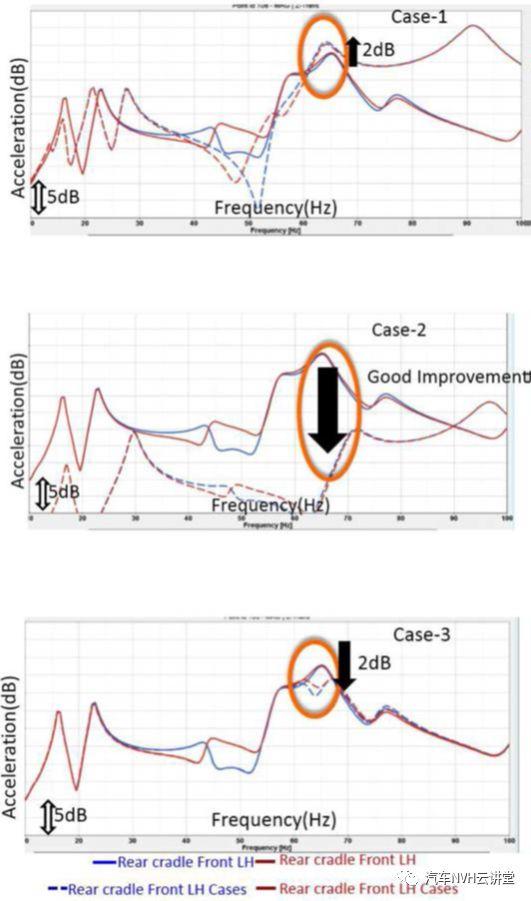
图11不同方案下计算响应
下一步的评估是建立装配模型从传动系统和修剪的车身模型,完整的四轮驱动系统连接到整车适当的位置。如图12所示,进一步计算了中间座椅位置的触觉响应。对于在副车架位置(即案例-2和案例-3)具有较低响应的案例,还提取了座椅加速度。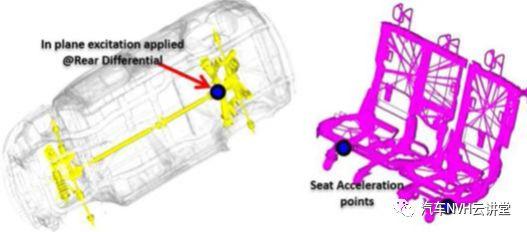
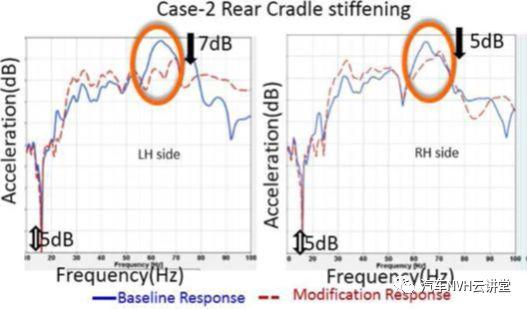
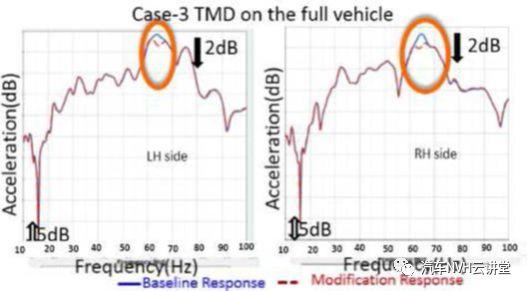
如图13(a)和13(b)所示,在有问题的频带,案例2的触觉响应改善了5~7db。在案例-3中,在有问题的频带观察到2dB改善此外,可以得出结论,车身对来自支架附着点的问题频带放大响应中的传动系激励敏感.通过振动声学分析,建立了用于修边体内部噪声研究的振动声学模型图14所示为53Hz时的声腔振型。该振型为纵向振型,节点位于中间座椅,反节点位于驾驶员和后排乘客位置在50赫兹左右出现小峰值,这可归因于在驾驶员和后排乘客位置能量含量较高的空腔。虽然在64Hz的问题频率下没有空腔模式,但响应(SPL)足够高,足以感知轰鸣噪声。在垂直面内激励下,计算了中间乘客的整车乘员舱噪声水平如图15所示,不同的峰值出现在基线响应中。通过案例2和案例3中提到的修改,在有问题的频带中看到了主要的SPL改进,本文所开发的方法在不使用复杂非线性多体系统的情况下解决了动力传动系轰鸣问题,可以用基本的线性FEModel系统给出AWD解。
为解决AWD传动系统的振动和内部噪声问题进行了分析。为解决全轮驱动样机在程序后期识别出的噪声和振动问题,开发了一套程序通过测试测量,确定了问题的根本原因是特定的操作偏差形状。解决典型的传动系统问题需要复杂的非线性MDB模型,在这一过程中,采用简化的线性模型来匹配试验行为为减少系统级响应,制定了进一步的快速解决方案,因此通过简化线性有限元模型和解决方案,可以在尽可能短的时间内改善了客户感知到的NVH。1. Wellmann T., Govindswamy K., Eisele. G.,“Driveline boom interior noise prediction based on Multi Body SimulationModel.”2. Du, H., Frederiksen, M., and Happel, S.,"Vibration Modeling and Correlation of Driveline Boom for TFWD/AWDCrossover Vehicles," SAE Technical Paper 2003-01-1495, 2003, doi:10.4271/2003-01-1495.3. Vasudeva Rao S and Soundararajan. S.,“Optimizing vehicle NVH characteristics for driveline integration.”4. Jones Paul G., University of Illinois.,“Torsional Vibrations in Drive Lines.” Definitions/AbbreviationsCAE - Computer Aided EngineeringNVH - Noise Vibrations & HarshnessMDB - Multi Body Dynamics.ODS - Operation Deflection ShapeN&V - Noise and VibrationPTU - Power Transfer UnitU Joint - Universal JointCV Joint - Constant Velocity JointRPM - Revolutions Per MinuteMPC - Multi Point ConstraintSPL - Sound Pressure Level
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-12
最近编辑:2年前



































