基于传递振动加速度最小的悬置优化方法研究
摘要:以某型四缸直列汽车在稳态工况下的传递振动加速度为目标函数,基于整车实测数据,应用粒子群算法对悬置刚度参数进行优化,使得由动力总成传递到驾驶室主驾驶座椅处振动加速度最小。同时对动力总成悬置系统的刚体振动模态频率和位移等加以约束。基于整车与台架发动机振动测试,将台架与整车测试辨识出的等效激振力进行了对比,证明了辨识方法的可行性。优化设计后,传递振动加速度有了明显的改善,验证了该方法的有效性,该方法可应用于悬置系统的优化设计。 关键词:动力总成;悬置系统;优化设计;传递振动加速度;粒子群算法
随着汽车的普及与发展,作为反应乘坐舒适性指标的车内振动与噪声,越来越引起人们的关注[1]。动力总成作为整车最大的振源之一[2-3],其隔振及约束系统的有效性直接关系到驾驶员和乘客的舒适性及车辆运行的平顺度。随着汽车轻量化的发展,悬置元件的优化问题也越来越成为国内外研究人员的关注重点。 动力总成悬置系统的优化参数一般包括悬置元件的安装坐标、安装倾角及刚度[2],而对于已经量产的汽车而言,优化一般不改变发动机动力总成的参数特性,因此最有效的方式是对悬置的刚度进行优化设计[4]。悬置系统优化在结构上可选择解耦布置[5-6]以实现主要振动的完全解耦,但结构要求较为苛刻。目前优化中常考虑在扭矩轴(TRA)坐标系中,使在扭矩轴方向的模态与其他方向进行解耦[7]。另一种思路是采用能量解耦方法[2,3,8-10],该方法可以实现任意六个自由度方便解耦,应用较为广泛。有关学者也提出考虑多目标[3]或综合优化目标[11]设计的方法或考虑动力总成传递到车身动反力[12]或能量功率流[13]的优化方法,为悬置优化设计提供了一个新的研究思路。但是,上述方法在研究过程中常常没有考虑到系统实际的响应,结果不一定能够满足实际要求。 因此,本文以动力总成传递到汽车座椅的加速度振动响应为目标函数,考虑到座椅处加速度响应对舒适性有较大影响,因此物理意义更为明确。将悬置简化为弹性节点,可以将动力总成和车身耦合振动考虑在内,同时以辨识出的整车实际发动机激振力为输入,采用粒子群算法对悬置刚度参数进行优化。通过台架与整车的等效激振力辨识结果的对比,验证了激振力辨识的准确性。经过优化后,通过和初始系统的对比,动力总成传递到驾驶室座椅处的振动加速度有了很大的改善,验证了该方法对悬置优化设计的有效性,该方法也可应用于一般隔振系统中隔振元件的优化设计中。 动力总成的激振力主要通过悬置安装点传递到车身,由于研究对象采用三个悬置,考虑到动力总成和车身的耦合,因此将悬置安装点视为弹性节点,以该三个弹性节点之间的导纳函数  来代表车身的动特性。结合导纳函数可建立整车耦合振动模型,动力总成悬置系统与车身的15自由度简化模型[13]如图1所示。采用拉格朗日方法可得到系统的振动微分方程。
来代表车身的动特性。结合导纳函数可建立整车耦合振动模型,动力总成悬置系统与车身的15自由度简化模型[13]如图1所示。采用拉格朗日方法可得到系统的振动微分方程。 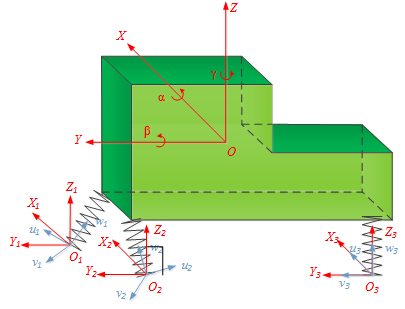
考虑到发动机各支点位置相距较远,可忽略悬置的扭转弹性。简化模型中被视为刚体的动力总成具有6个自由度,左、右和后悬置处的三个弹性节点共计9个自由度。以动力总成的质心坐标系O-XYZ为标准,三个悬置点处的局部坐标系O1-u1v1w1、O2-u2v2w2、O3-u3v3w3的坐标轴见图1所示。设广义坐标为  ,其中,
,其中,  表示动力总成的位移矢量,
表示动力总成的位移矢量,  表示左悬置、右悬置、后悬置与车架三个弹性节点的位移矢量。
表示左悬置、右悬置、后悬置与车架三个弹性节点的位移矢量。
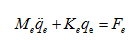
(1)
方程(1)中,  分别是系统质量矩阵和刚度矩阵,可以由系统动能表达式和系统势能表达式推导而来。
分别是系统质量矩阵和刚度矩阵,可以由系统动能表达式和系统势能表达式推导而来。  是激振力矢量。
是激振力矢量。
 (2)
(2)
其中,  表达式如下:
表达式如下:
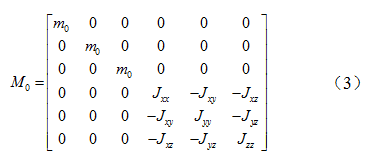
式(3)中,m0为动力总成质量,  为动力总成的各个转动惯量和惯性积,均可通过测试得出。
为动力总成的各个转动惯量和惯性积,均可通过测试得出。
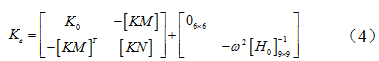
其中,  为加速度导纳矩阵,可由锤击法或激振器激励试验获得。
为加速度导纳矩阵,可由锤击法或激振器激励试验获得。  和
和  表达如下:
表达如下:
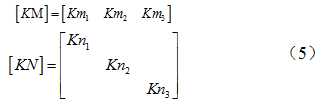
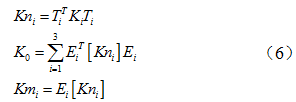
其中,  表示动力总成刚体质心的运动引起刚体上悬置点三个方向运动的位移转移矩阵。
表示动力总成刚体质心的运动引起刚体上悬置点三个方向运动的位移转移矩阵。  矩阵表示每个悬置点处的广义坐标系与局部坐标系之间的夹角欧拉旋转矩阵。
矩阵表示每个悬置点处的广义坐标系与局部坐标系之间的夹角欧拉旋转矩阵。  表示第
表示第  个悬置在局部坐标系下的三个方向的刚度组成的刚度系数矩阵。其中,由于橡胶在低频振动状态下阻尼特性可看作结构阻尼[15],因此此处采用复数刚度表示橡胶特性,本文中通过动刚度测试,选择结构的损耗因子
个悬置在局部坐标系下的三个方向的刚度组成的刚度系数矩阵。其中,由于橡胶在低频振动状态下阻尼特性可看作结构阻尼[15],因此此处采用复数刚度表示橡胶特性,本文中通过动刚度测试,选择结构的损耗因子  。 在发动机激振力辨识过程中,将车架视为刚体,动力总成悬置系统只包含
。 在发动机激振力辨识过程中,将车架视为刚体,动力总成悬置系统只包含  的6个自由度,在质心坐标系下,其运动微分方程为
的6个自由度,在质心坐标系下,其运动微分方程为
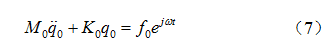
每个悬置与发动机连接点在质心坐标系下的位移向量为  。发动机悬置处加速度向量
。发动机悬置处加速度向量  。
。  表示动力总成质心到三个发动机悬置点的转移矩阵组成的矩阵。
表示动力总成质心到三个发动机悬置点的转移矩阵组成的矩阵。
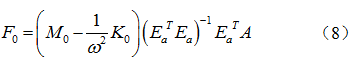
分别在台架与整车上进行发动机等效激振力辨识实验,共计六种工况,见表1。
为了验证等效激振力辨识结果的可靠性,分别在整车与发动机动力总成台架上进行测试,其中,发动机台架实验测试与整车测试现场见图2所示。为了降低加速度传感器安装位置所带来的误差,整车测试中加速度安装位置与台架保持一致。通过分别测试悬置上下端点处的加速度响应来减小整车测试中汽车行驶带来的影响。 
图 2测试现场测试图
其中怠速工况下误差分析见表2所示。此处定义误差为: 
以怠速工况为例,台架测试与整车测试对比结果见图3-图5,可知,对比表2可知,在怠速工况下,等效激振力辨识结果两者结果偏差较小,误差均在13%以内。由此可知,发动机动力总成辨识结果有很好的可靠性,证明了辨识过程的有效性。 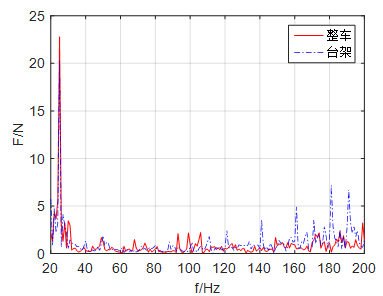
图 3  辨识结果对比
辨识结果对比 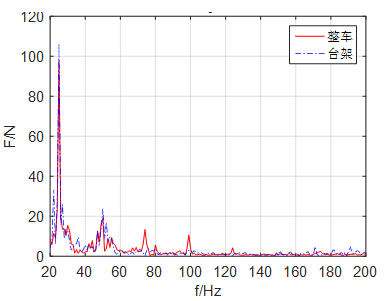
图 4  辨识结果对比 图 5
辨识结果对比 图 5  辨识结果对比 由测试辨识出的发动机激振力辨识结果
辨识结果对比 由测试辨识出的发动机激振力辨识结果  和振动微分方程(1),可得该系统的稳态响应为:
和振动微分方程(1),可得该系统的稳态响应为: 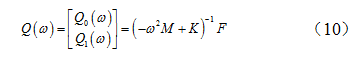
式(10)中,  为三个悬置点处的稳态响应,由此可求得悬置处的支反力稳态响应为:
为三个悬置点处的稳态响应,由此可求得悬置处的支反力稳态响应为: 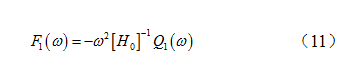
通过锤击测试得到悬置点处的9个方向作用力到驾驶室主驾驶座椅处加速度响应的传递函数  ,由此可得到座椅加速度响应为:
,由此可得到座椅加速度响应为: 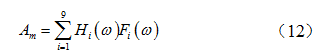
由于频域分析方法得到的是加速度的频谱,根据帕塞瓦尔定理,因为只关心20Hz-200Hz频带范围,而且该频带之外的加速度幅值较小,因此最终选取的目标函数为 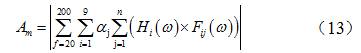
其中  为加权因子,
为加权因子,  是第
是第  个工况下对应的悬置支反力稳态响应结果。 优化算法使用粒子群优化算法,算法程序框图见图6所示。粒子群优化算法是一种基于迭代的优化求解算法,系统初始化生成一组随机解,然后通过一定的机制迭代直到收敛得到最优解。由于它的速度快、精度高、实现容易等特点,粒子群优化算法目前已被广泛应用于神经网络训练、多目标组合优化中[16]。
个工况下对应的悬置支反力稳态响应结果。 优化算法使用粒子群优化算法,算法程序框图见图6所示。粒子群优化算法是一种基于迭代的优化求解算法,系统初始化生成一组随机解,然后通过一定的机制迭代直到收敛得到最优解。由于它的速度快、精度高、实现容易等特点,粒子群优化算法目前已被广泛应用于神经网络训练、多目标组合优化中[16]。 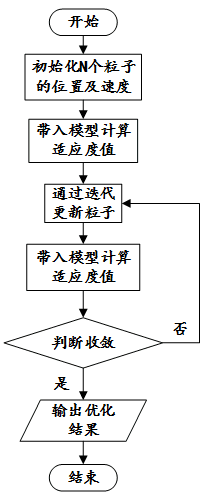
(1)刚度约束:悬置刚度太软会导致发动机与车身相对位移增大,易引起部件之间的碰撞,刚度太硬则会导致悬置和发动机为刚性连续体,会引起驻波效应[12]。同时考虑到制造方便,本文中左悬置和右悬置橡胶的刚度剪切比设定为3~8之间[2,6]。为保证支撑发动机动力总成而不产生多大静位移,需约束最大位移量[3-4],此时要求对橡胶悬置刚度进行相应约束。 (2)固有频率约束:考虑到当激励频率大于  倍的系统固有频率时,系统才能起到隔振作用。因此动力总成绕曲轴方向扭转的固有频率应小于发动机怠速时的点火脉冲频率的
倍的系统固有频率时,系统才能起到隔振作用。因此动力总成绕曲轴方向扭转的固有频率应小于发动机怠速时的点火脉冲频率的  倍[2,6,8]。因此选取频率:
倍[2,6,8]。因此选取频率:  ,同时考虑到相邻两阶固有频率不能靠得太近。
,同时考虑到相邻两阶固有频率不能靠得太近。
将优化前初始系统和优化后系统作对比,结果见图7和图8所示。由图可知,经过优化后的系统,动力总成传递到主驾驶座椅处的加速度响应有了很大的降低,共降低2.5dB左右,优化效果明显。 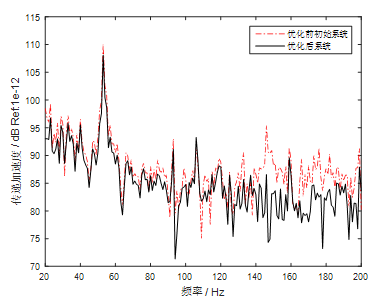
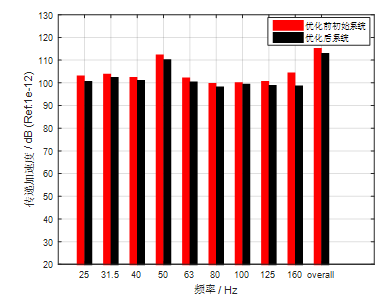
同时,考虑到悬置加工误差,因此需对动力总成-悬置系统进行稳健性分析,稳健性结果表明,在悬置加工误差在  情况下,优化后的系统传递加速度均相较初始系统有很大的优化效果,说明结果具有很好的稳健性。 本文主要对某型四缸直列发动机汽车悬置系统进行了优化设计,使得动力总成传递到驾驶室座椅处的振动加速度有了很大的改善。由于座椅处加速度响应直接影响到乘客的舒适性体验,对汽车NVH尤为重要,因此优化结果具有一定的工程应用价值,同时在优化中也考虑到了动力总成和车身处的耦合,并以实际测试辨识出的激振力为输入,更符合实际工况。本文最后使用粒子群优化算法进行求解计算,结果最终满足优化要求,具有工程参考意义。 【免责声明】本公 众 号所刊载上述内容,资料等来自于网络、社会实践、个人总结、技术论坛等,对文中陈述、观点判断保持中立,不对所包含内容的准确性、可靠性或完整性提供任何明示或暗示的保证。如果您认为我们的授权或者来源标注与事实不符,请告知我们,我们及时修订或删除。谢谢大家的关注。
情况下,优化后的系统传递加速度均相较初始系统有很大的优化效果,说明结果具有很好的稳健性。 本文主要对某型四缸直列发动机汽车悬置系统进行了优化设计,使得动力总成传递到驾驶室座椅处的振动加速度有了很大的改善。由于座椅处加速度响应直接影响到乘客的舒适性体验,对汽车NVH尤为重要,因此优化结果具有一定的工程应用价值,同时在优化中也考虑到了动力总成和车身处的耦合,并以实际测试辨识出的激振力为输入,更符合实际工况。本文最后使用粒子群优化算法进行求解计算,结果最终满足优化要求,具有工程参考意义。 【免责声明】本公 众 号所刊载上述内容,资料等来自于网络、社会实践、个人总结、技术论坛等,对文中陈述、观点判断保持中立,不对所包含内容的准确性、可靠性或完整性提供任何明示或暗示的保证。如果您认为我们的授权或者来源标注与事实不符,请告知我们,我们及时修订或删除。谢谢大家的关注。 往期相关推荐
相关文章,在仿真秀官网搜索:
干货│基于ABAQUS的橡胶悬置胶合件刚度仿真计算
基于MATLAB+ISIGHT的悬置系统敏感性分析
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-12
最近编辑:2年前
作者推荐

 来代表车身的动特性。结合导纳函数可建立整车耦合振动模型,动力总成悬置系统与车身的15自由度简化模型[13]如图1所示。采用拉格朗日方法可得到系统的振动微分方程。
来代表车身的动特性。结合导纳函数可建立整车耦合振动模型,动力总成悬置系统与车身的15自由度简化模型[13]如图1所示。采用拉格朗日方法可得到系统的振动微分方程。 
 ,其中,
,其中,  表示动力总成的位移矢量,
表示动力总成的位移矢量,  表示左悬置、右悬置、后悬置与车架三个弹性节点的位移矢量。
表示左悬置、右悬置、后悬置与车架三个弹性节点的位移矢量。 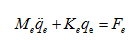
 分别是系统质量矩阵和刚度矩阵,可以由系统动能表达式和系统势能表达式推导而来。
分别是系统质量矩阵和刚度矩阵,可以由系统动能表达式和系统势能表达式推导而来。  是激振力矢量。
是激振力矢量。  (2)
(2) 表达式如下:
表达式如下: 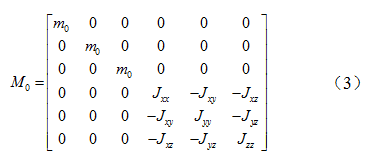
 为动力总成的各个转动惯量和惯性积,均可通过测试得出。
为动力总成的各个转动惯量和惯性积,均可通过测试得出。 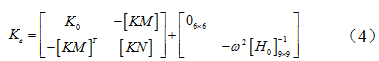
 为加速度导纳矩阵,可由锤击法或激振器激励试验获得。
为加速度导纳矩阵,可由锤击法或激振器激励试验获得。  和
和  表达如下:
表达如下: 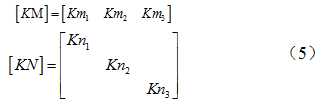
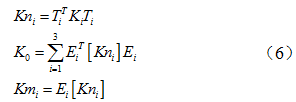
 表示动力总成刚体质心的运动引起刚体上悬置点三个方向运动的位移转移矩阵。
表示动力总成刚体质心的运动引起刚体上悬置点三个方向运动的位移转移矩阵。  矩阵表示每个悬置点处的广义坐标系与局部坐标系之间的夹角欧拉旋转矩阵。
矩阵表示每个悬置点处的广义坐标系与局部坐标系之间的夹角欧拉旋转矩阵。  表示第
表示第  个悬置在局部坐标系下的三个方向的刚度组成的刚度系数矩阵。其中,由于橡胶在低频振动状态下阻尼特性可看作结构阻尼[15],因此此处采用复数刚度表示橡胶特性,本文中通过动刚度测试,选择结构的损耗因子
个悬置在局部坐标系下的三个方向的刚度组成的刚度系数矩阵。其中,由于橡胶在低频振动状态下阻尼特性可看作结构阻尼[15],因此此处采用复数刚度表示橡胶特性,本文中通过动刚度测试,选择结构的损耗因子  。
。  的6个自由度,在质心坐标系下,其运动微分方程为
的6个自由度,在质心坐标系下,其运动微分方程为 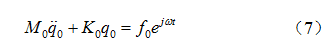
 。发动机悬置处加速度向量
。发动机悬置处加速度向量  。
。  表示动力总成质心到三个发动机悬置点的转移矩阵组成的矩阵。
表示动力总成质心到三个发动机悬置点的转移矩阵组成的矩阵。 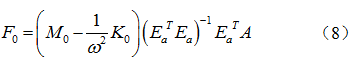


 (N)
(N)  (N)
(N)  (N)
(N) 


 辨识结果对比
辨识结果对比 
 辨识结果对比
辨识结果对比 
 辨识结果对比
辨识结果对比  和振动微分方程(1),可得该系统的稳态响应为:
和振动微分方程(1),可得该系统的稳态响应为: 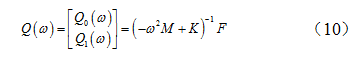
 为三个悬置点处的稳态响应,由此可求得悬置处的支反力稳态响应为:
为三个悬置点处的稳态响应,由此可求得悬置处的支反力稳态响应为: 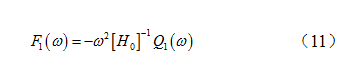
 ,由此可得到座椅加速度响应为:
,由此可得到座椅加速度响应为: 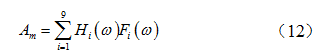
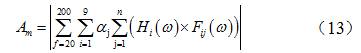
 为加权因子,
为加权因子,  是第
是第  个工况下对应的悬置支反力稳态响应结果。
个工况下对应的悬置支反力稳态响应结果。 
 倍的系统固有频率时,系统才能起到隔振作用。因此动力总成绕曲轴方向扭转的固有频率应小于发动机怠速时的点火脉冲频率的
倍的系统固有频率时,系统才能起到隔振作用。因此动力总成绕曲轴方向扭转的固有频率应小于发动机怠速时的点火脉冲频率的  倍[2,6,8]。因此选取频率:
倍[2,6,8]。因此选取频率:  ,同时考虑到相邻两阶固有频率不能靠得太近。
,同时考虑到相邻两阶固有频率不能靠得太近。 

 情况下,优化后的系统传递加速度均相较初始系统有很大的优化效果,说明结果具有很好的稳健性。
情况下,优化后的系统传递加速度均相较初始系统有很大的优化效果,说明结果具有很好的稳健性。 




