含防扭拉杆的悬置系统硬点选取对解耦分析及工况计算结果影响的研究

平衡扭矩轴系统即TRA三点悬置布置系统，以左右悬置为承载悬置，以后悬置为抗扭悬置，是当前很多中小型乘用车广泛使用的一种悬置布置方式。由于抗扭悬置有两个衬套，就存在两个硬点位置，本文将研究一下硬点选取对解耦分析以及工况计算的结果的影响情况。

图1三点TRA悬置系统

1. 解耦分析及工况计算时硬点选取对计算结果影响的研究

由于抗扭拉杆有大小两个衬套，就有两个硬点位置，在不同的计算工况下，选取的硬点位置是有所不同的，如果是解耦分析，取的是大端衬套硬点位置，这是由于已经把抗扭拉杆的大小衬套的刚度都一起等效到了大端的缘故，什么是等效刚度以及如何通过计算获取可查阅公 众 号文章，也可到IND4汽车人平台购买我上传的系列课程。

本文所研究车型的动力总成的质量为174.38kg，质心在汽车坐标系的坐标为（701.99，67.35，567.5）mm，在动力总成质心坐标系op-xpypzp中的转动惯量（Ixx，Iyy，Izz）和惯性积（Ixy，Iyz，Izx）见表1。各悬置在汽车坐标系的安装位置见表2，悬置设计刚度见表3。

表1质量与惯量

表2 悬置硬点位置

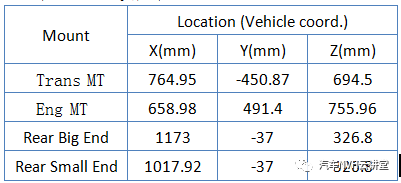
表3悬置设计刚度表

下面给出分别使用大端和小端硬点计算的解耦计算的结果差异。

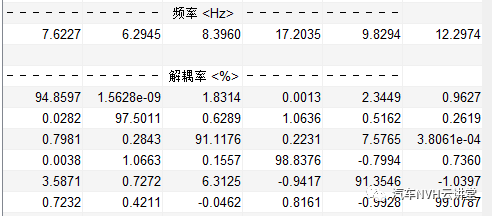
图2大端硬点的模态解耦分析结果

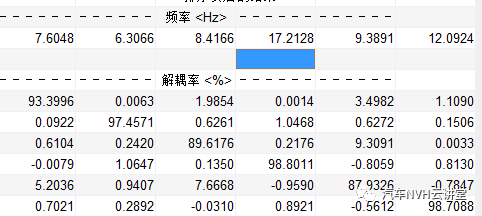
图3小端硬点的模态解耦分析结果

可知模态计算结果差异很小，但Z向及RYY解耦率有一定的影响.

2、硬点选取对载荷工况计算结果的影响

至于工况载荷计算，这里也分别选取了2种典型工况和4种极限工况，通过ADAMS模型（见图10）来计算动力总成的位移和各悬置在其弹性主轴方向的位移及力。进而来分析选取不同位置的计算结果差异。

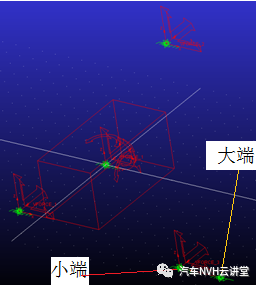
图4 28工况载荷计算模型

2.1典型工况

典型工况1为动力总成质心在yp方向有3mg的载荷（m为动力总成的质量，g为重力加速度）；典型工况2为动力总成质心在垂直方向有3.5mg的载荷，yp方向有2mg的载荷。两种工况下，作用在动力总成上的力和力矩见表1。利用不同拉杆模型（大端或小端）计算得到的动力总成位移和各悬置在弹性主轴方向的位移及力见表2到表5。

各种工况下作用在动力总成上的力和力矩见表11。利用不同的简化拉杆模型计算得到的动力总成位移及各悬置在其弹性主轴方向的位移及力见表12到表5。

表1典型载荷工况

表2典型工况1下的动力总成位移

表3典型工况1下的各悬置的位移及力

表4典型工况2下的动力总成位移

表5 典型工况2下的各悬置的位移及力

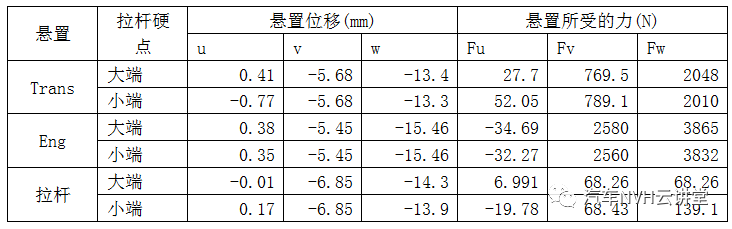
从表2和表4可知，在这两种典型工况下，不同拉杆模型下的动力总成位移基本相同。从表3和表5可知，在这两种典型工况下，主要受力的悬置都为Eng悬置和Trans悬置，且利用不同拉杆模型时，Eng悬置和Trans悬置的受力大小基本一致。同时，大端和小端模型的拉杆受力均较小。因此，当动力总成质心受Y向（侧向）或Z向（垂向）的典型工况力时，将拉杆简化为大端模型或小端模型时，动力总成的位移和各悬置的受力计算结果基本一致。

2.2极限载荷工况

本文选取2种极限载荷工况：（1）大扭矩工况：动力总成质心绕yp（曲轴）方向有大扭矩（发动机最大扭矩的15倍）；（2）碰撞工况：动力总成质心在X向有11mg的载荷。；（3）大侧向加速度工况：在Y向有5mg的载荷；（4）大垂直方向加速度工况：在Z向有5mg的载荷。

表6极限载荷工况列表

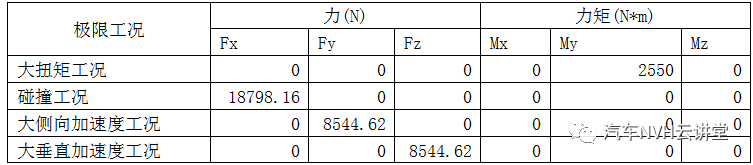
表7极限载荷工况下的动力总成位移

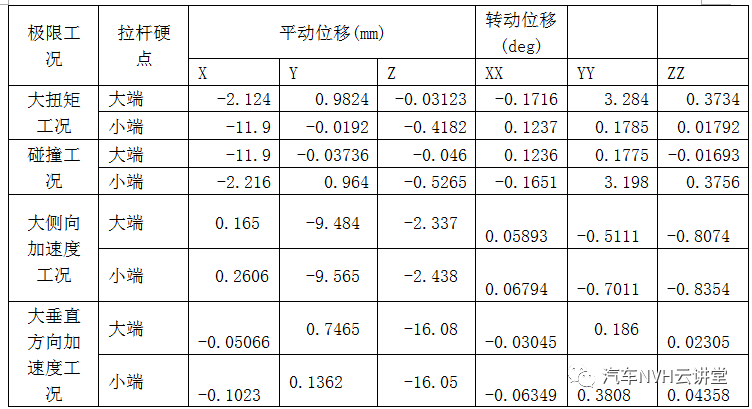
表8大扭矩工况下的各悬置的位移及力

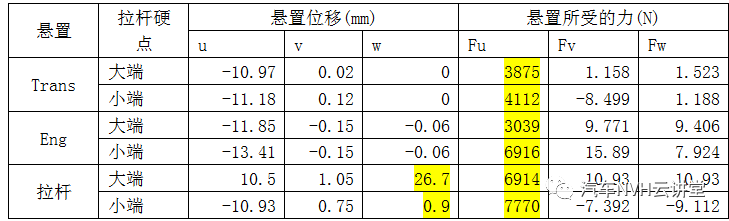
表9碰撞工况下的各悬置的位移及力

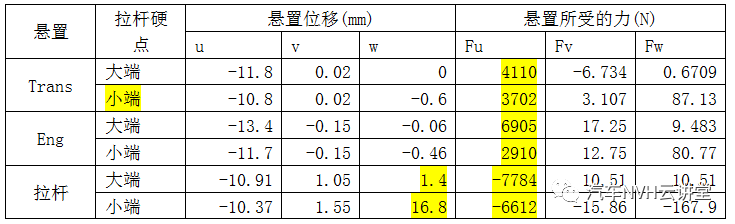
表10大侧向加速度工况各悬置的位移及力

表11大垂直加速度工况各悬置的位移及力

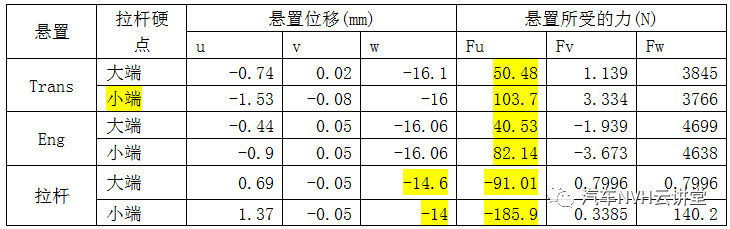
从表7可知，当动力总成受力为大侧向加速度工况或大垂直方向加速度工况时，利用不同拉杆模型计算得到的动力总成位移基本相同。从表8和表9可知，此时Eng悬置和Trans悬置是主要受力悬置，且不同拉杆模型下的Eng悬置和Trans悬置的受力大小基本一致。同时，采用大端和小端模型的拉杆受力均较小。因此，大侧向加速度工况或大垂直方向加速度工况，采用拉杆的大端模型和小端模型时，动力总成的位移和各悬置的受力计算结果基本一致。

从表7可知，当动力总成受力为大扭矩工况或碰撞工况时，利用拉杆的大端模型计算得到的动力总成在X向的平动位移（绝对值）以及YY向的转角与小端模型存在较大差异。从表8和表9可知，在这两种极限工况下，不同拉杆模型的主要受力方向均为u向，且受力大小还有一定差异，特别是发动机侧悬置的受力差异很大，其余方向差异不大。

1. 结论

当动力总成受侧向或垂直方向载荷（包括典型载荷和极限载荷）时，利用不同拉杆模型计算得到的动力总成位移和各悬置的受力基本一致。但当动力总成受力为大扭矩工况或碰撞工况时，不同拉杆模型对动力总成位移的计算结果则有较大影响，小端拉杆模型的动力总成位移更大。同时，不同拉杆模型在w方向的受力大小也有明显的不同，小端拉杆模型的受力更大。