电机缺陷/故障对振动噪声的影响
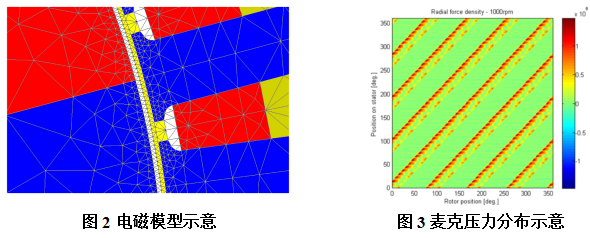
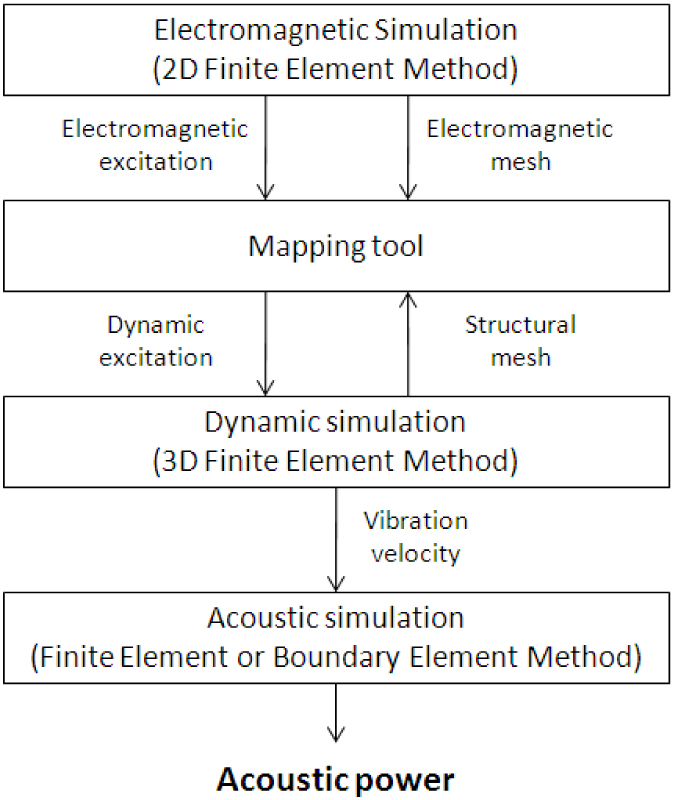
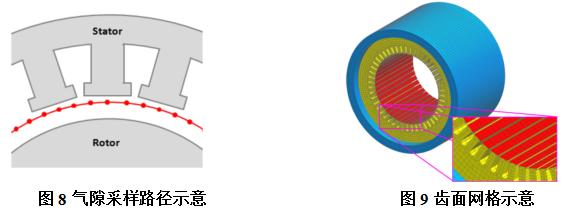
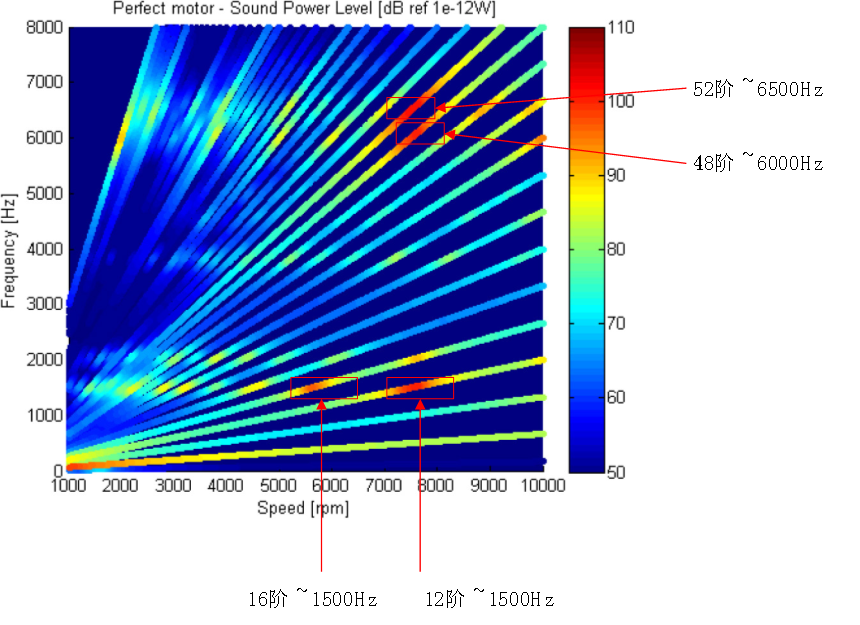
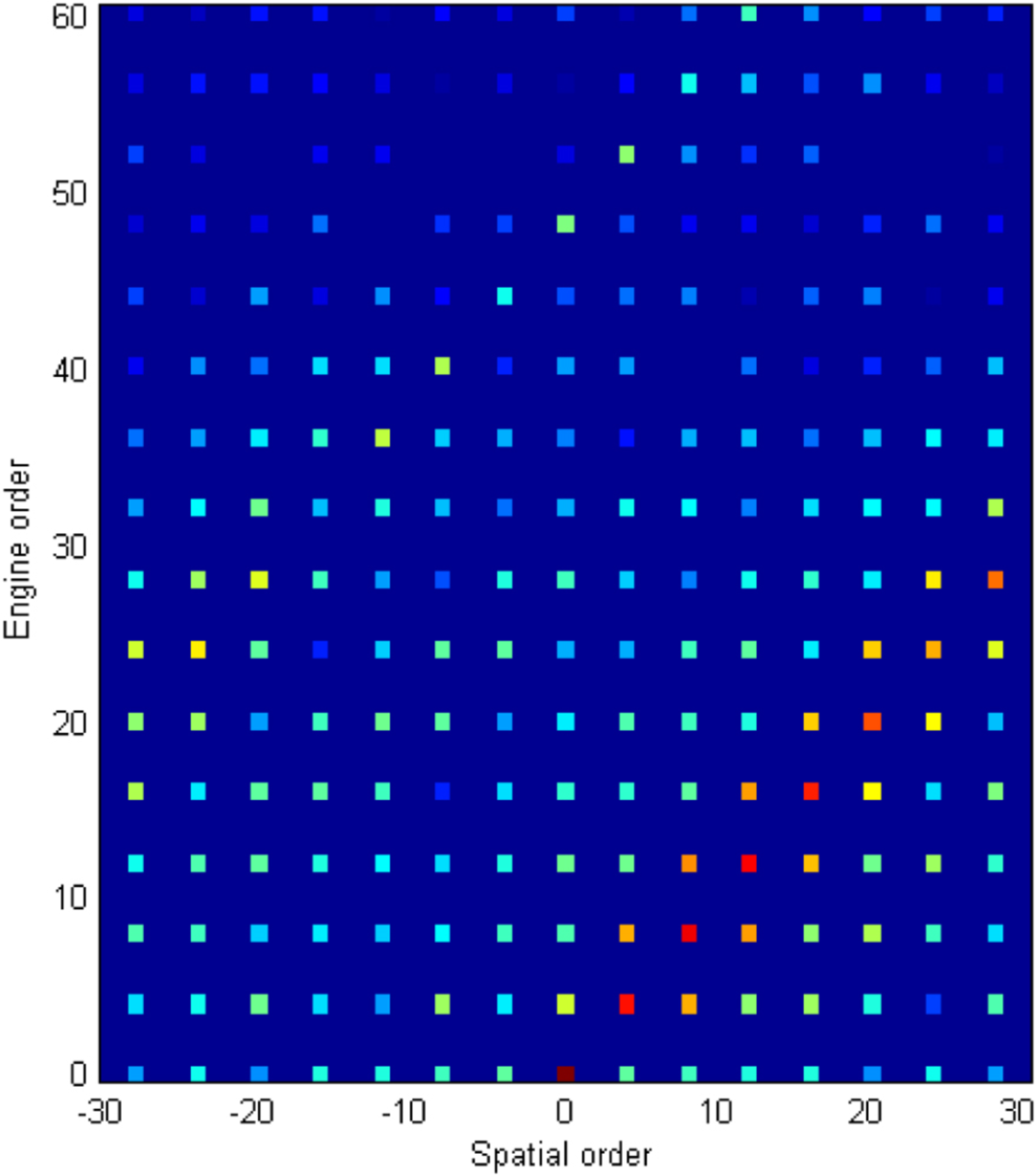
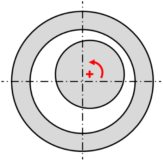
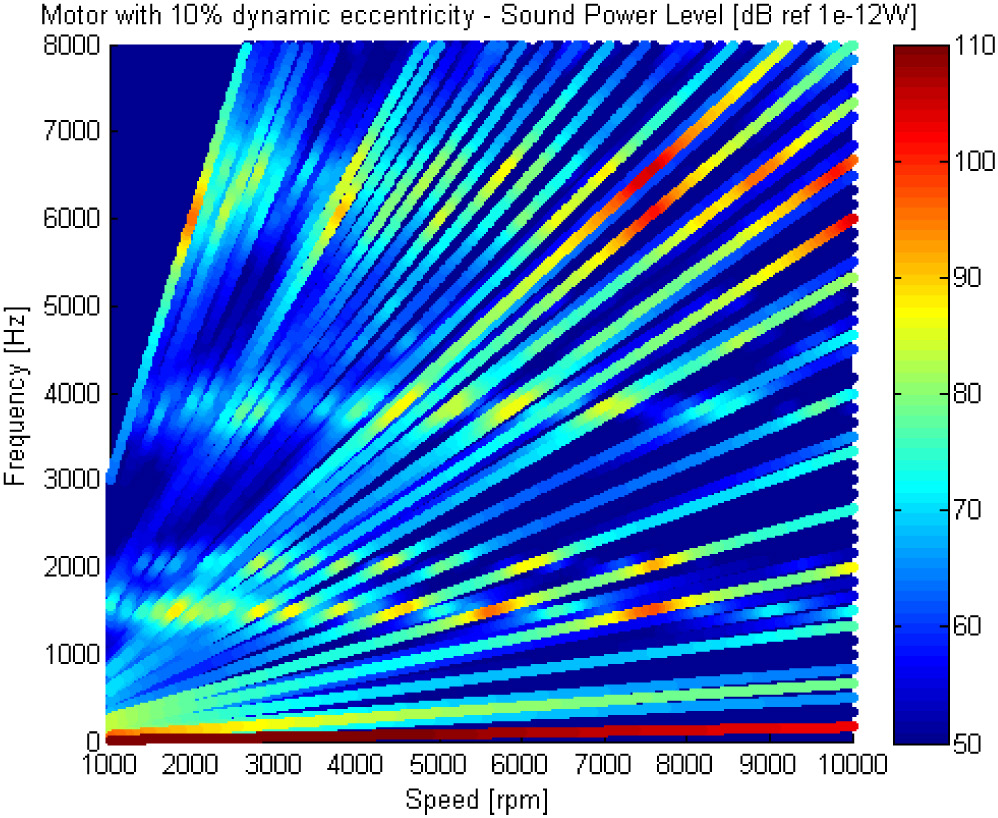
本文首先通过有限元计算方法计算电机阶次噪声,借助电磁力阶次及模态计算结果,分析电磁力阶次与结构模态的耦合特征。在此基础上引入匝间短路、静态偏心、动态偏心三种缺陷,分别对比其电磁力阶次特征与理想电机的差异。并分析对比缺陷导致的电磁噪声差异对比及原因。 计算中选择某表贴式永磁同步电机为例。电机基本信息如表1所示: 电磁模型示意如下图1-2所示,气隙麦克思维压力分布如图3所示。 简化后的电机模型如下图4-5所示。本研究中主要关注径向激励对结构圆柱模态的影响。 在电磁模型和结构有限元模型基础上,提取气隙麦克斯韦压力并将其映射到结构有限元网格上,计算结构在电磁激励下的振动噪声响应。计算流程见下图7所示。 借助图7中计算流程,提取气隙麦克思维压力得到电磁力空间及频率阶次特征如图10所示。在此基础上计算得到噪声结果如图11所示。 结合电磁力阶次特征及噪声计算结果,对主要噪声峰值进行简要分析:12阶~1500Hz处峰值为0阶电磁力激励圆柱二阶模态引起的强迫振动;16阶~1500Hz处峰值为+4阶电磁力激励圆柱二阶模态引起的强迫振动;48阶~6000Hz为0阶电磁力与圆柱0阶模态产生的共振;52阶~5200rpm为+4阶电磁力与结构4阶模态产生的共振。 在电磁有限元模型中提取气隙电磁力得到电磁力阶次特征以及噪声结果如下图13所示: 对比电磁力阶次特征可以看出,增加短路缺陷后电磁力频率阶次特征与理想电机相同;空间阶次则被4,8调制。 从噪声曲线上可以看出,频率44阶处由于调制出了空间±4阶电磁力,导致圆柱4阶模态固有频率处出现噪声峰值;同样,频率48阶处,由于调制出了±4阶电磁力,其在4阶模态处同样出现新的噪声峰值。 静偏心示意如下图15所示,即转子几何中心与定子几何中心不重合,转子旋转中心为转子几何中心。静态偏心时,气隙磁导在时间上不变,在空间上由于偏心的存在引入了新的谐波项。本计算中,设定偏心量为10%气隙厚度。 在电磁有限元模型中提取气隙电磁力得到电磁力阶次特征以及噪声结果如下图16所示: 对比电磁力阶次特征可以看出,增加静态偏心缺陷后电磁力频率阶次特征与理想电机相同;空间阶次则被±1调制。 由噪声计算结果可以看出,由于±4阶空间电磁力被±1调制后,出现新的±3阶空间电磁力,因而在结构3阶模态~3800Hz处噪声峰值出现一定程度提高。由于偏心量相对较小,因而3阶模态处噪声峰值仍然显著小于结构4阶及0阶共振频率处。 动偏心示意如下图18所示,即转子几何中心与定子几何中心不重合,转子旋转中心为定子几何中心。动态偏心时,气隙磁导同时引入时间及空间谐波项。本计算中,设定偏心量为10%气隙厚度。 在电磁有限元模型中提取气隙电磁力得到电磁力阶次特征以及噪声结果如下图19所示: 对比电磁力阶次特征可以看出,增加动态偏心缺陷后电磁力频率阶次特征及空间阶次均被±1调制。 对比噪声计算结果可以看出,动态偏心下,由于频率阶次被±1调制,导致图上出现大量边频,如33,39,45,51等阶次;由于空间阶次被±1调制,导致出现空间±3阶电磁力出现,因而圆柱3阶模态处噪声特征与静态偏心下相似。随着偏心量的提高,变频处及圆柱3阶模态处噪声峰值将进一步提高。 电机电磁振动问题是电磁力频率阶次和空间阶次,结构模态阶次与频率耦合作用的结果。当频率一致且阶次一致时,电磁力与结构将存在显著共振,进而导致严重的振动噪声问题。 分了三种缺陷类型对电磁力及振动噪声的影响,可得到以下结论: a) 匝间短路导致的不平衡反应在的电磁力阶次特征上:电磁力空间阶次以电机极数2p进行调制;频率阶次不变; b) 静偏心反应在的电磁力阶次特征上:电磁力空间阶次以±1进行调制;频率阶次不变; c) 动偏心反应在的电磁力阶次特征上:电磁力空间阶次以±1进行调制;频率阶次以±1进行调制。 往期相关推荐
相关文章,在仿真秀官网搜索:
基于LMS Test.Lab动力吸振器在整车振动噪声控制中的应用
本公 众 号新能源汽车相关文章汇总(截止到2020年6月15日)
618钜惠即将结束!悬置系统仿真系列视频课程活动期间优惠学习!
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-13
最近编辑:1年前
作者推荐