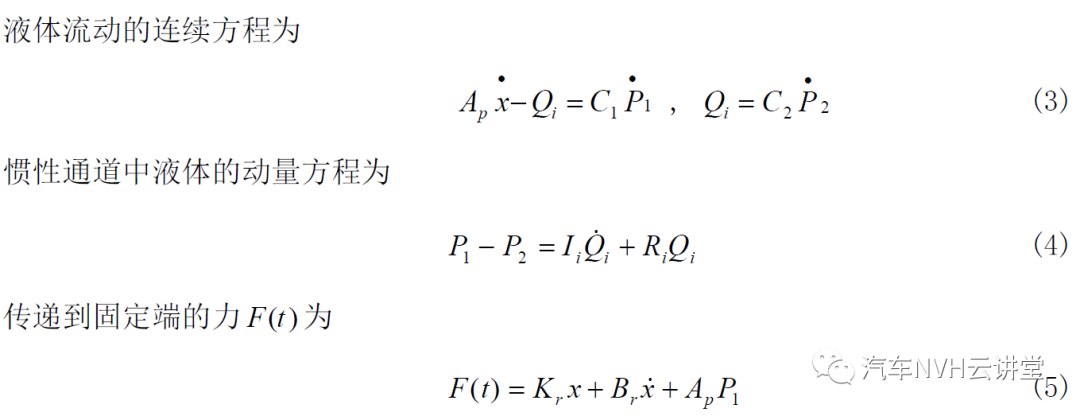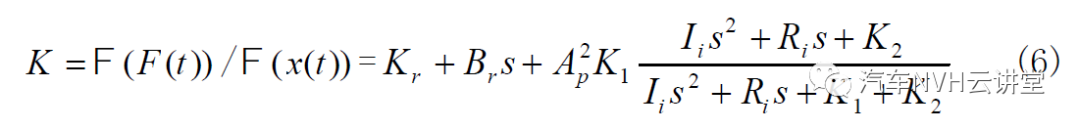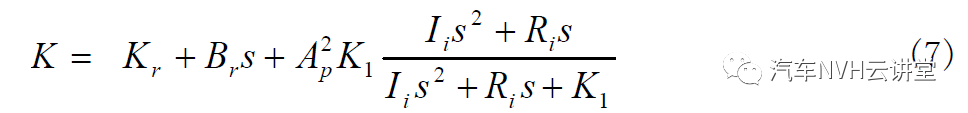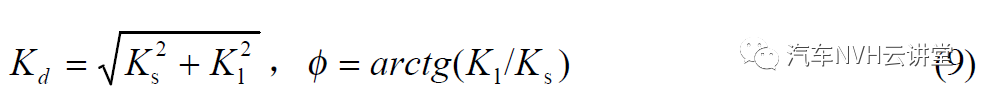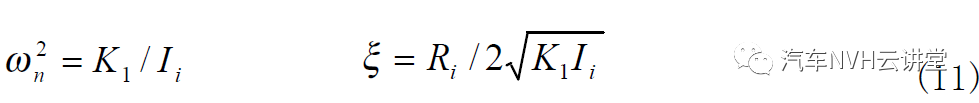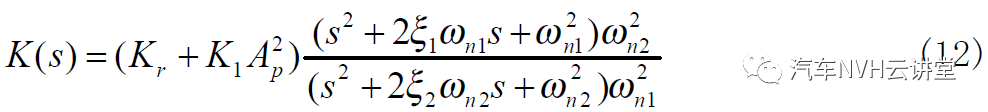液阻悬置集总参数模型动态特性的仿真与影响因素分析
摘要:集总参数模型是汽车动力总成液阻悬置动态特性仿真分析的的重要模型,本文的介绍了液阻悬置动态特性分析的集总参数模型及其特点,计算分析了集总参数模型中的物理参数的变化对液阻悬置动态特性影响的一般规律,讨论了物理参数的变化特性及其计算与实验方法的特点与局限性。以惯性通道式液阻悬置为例,建立液阻悬置动态特性分析的集总参数模型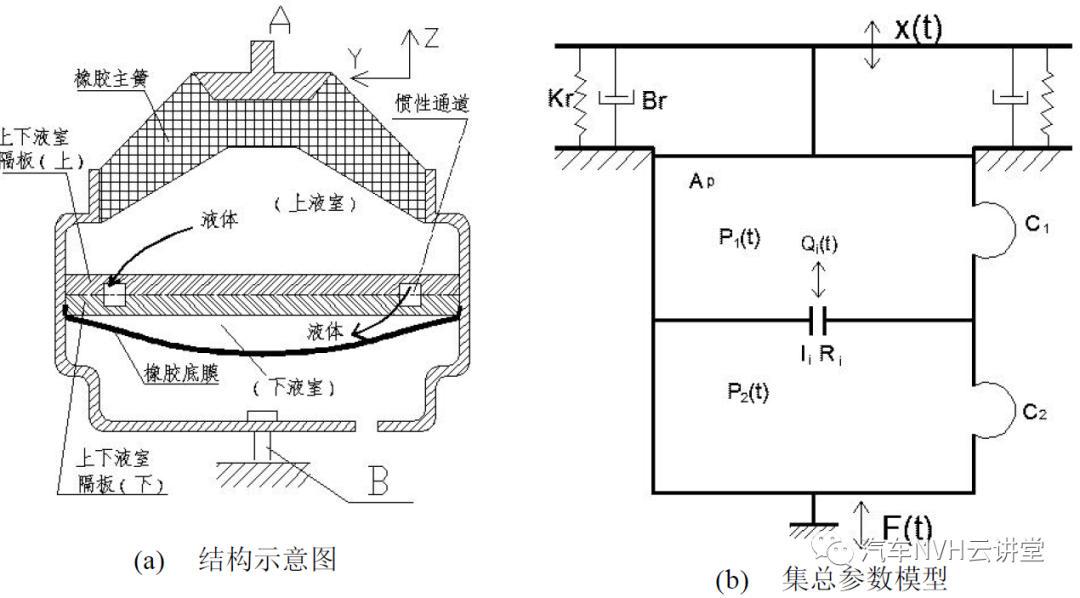
惯性通道式液阻悬置的结构示意图和集总参数力学模型如图 1 所示。橡胶主簧的作用有二个,一是承受动力总成的静、动态载荷,因此具有刚度 K r 和阻尼 Br ,二是起到类似活塞的作用,使液体在上、下液室之间来回流动,用等效活塞面积 Ap 来表示其特性。另外,橡胶主簧在泵吸液体的过程中,有一定的膨胀变形,橡胶主簧的这种膨胀特性用上液室的体积柔度或者体积刚度来表示,体积刚度 K 的定义为: (1)
(1)
即体积刚度等于上液室压力的变化ΔP 与液室体积的变化ΔV 的比值,其单位为 N / m5。体积刚度的倒数称为体积柔度( C = 1/ K ),单位为 m5/ N。
橡胶底膜主要起密封作用,在液阻悬置工作时,有较大的膨胀变形,其膨胀特性用体积柔度C 2 表示(与此对应的体积刚度为 K 2 = 1/ C2 ),由于橡胶底膜的厚度很薄(通常为 2mm 左右),因此,可以认为 C 至少比C 大两个数量级[ ],或者认为下液室的体积刚度 K2 为零。惯性通道中液体的特性用集总参数 Ii 和 Ri表征,分别表示惯性通道中液体的质量惯性系数(又称液感,单位为 kg/ m4)和惯性通道对液体流动的流量阻尼系数(又称液阻,单位为 N.s/m5),此二参数的定义为 (2)
(2)
上式中, mi 为惯性通道中液体的质量(kg), p 为液体的密度, Li 为惯性通道的长度,
ξ为与速度的一次方成正比的阻尼系数(N.s/m), A 为惯性通道横截面的面积(m2)。集总参数模型中的系统变量有:施加于橡胶主簧上端的位移激励 x(t) 和传递到悬置固定端的动反力 F (t ) ;上、下液室的平均压力用 P1 (t) 和 P2 (t) 表示,液体流径惯性通道的流量用Qi (t ) 表示。
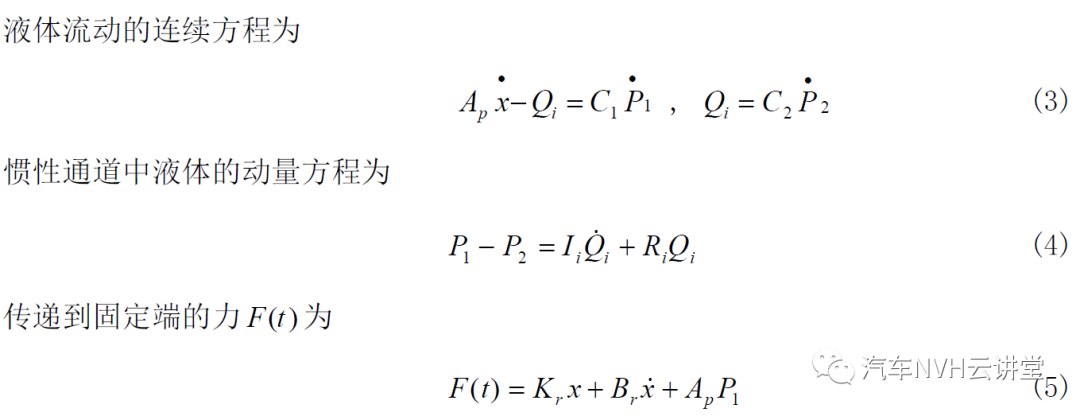
方程(3)~(5)为惯性通道式液阻悬置线型模型的一般表达式,它们仅适用于低频激励的情况。由方程(3)-(5)可得惯性通道式液阻悬置的复刚度为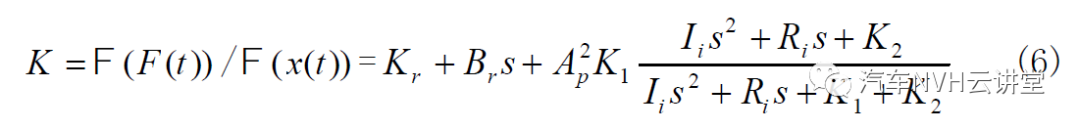
本文液阻悬置的底膜很薄(一般为 2mm 左右),主要起密封作用,因此,下液室的体积刚度 K 2 很小,可以忽略不计。令 K2 = 0,代入(3-44)式,有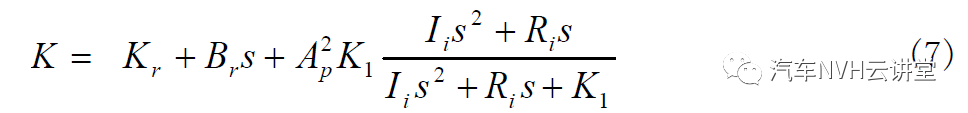
此公式与文献[ ]给出的惯性通道式液阻悬置的复刚度一样。假定正弦位移激励为x(t) = X 0 sin( m0t ) ,将 s = jω 带入(7)式,并进行简化即可得到液阻悬置在m = m0 时的复刚度上式中, K s 为存储刚度, Kl 为损失刚度,动刚度 Kd 和滞后角小 的定义为: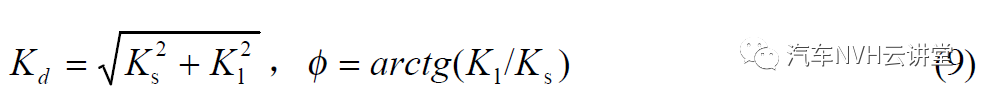
动刚度反应了在一定的激振频率下,响应力的幅值与激振位移的幅值比;而滞后角反应了位移滞后于力的角度,表征隔振元件阻尼的大小,工程上常用阻尼系数 C 表示,定义为:
由公式(8)~(10)可见,影响液阻悬置动态特性集总参数模型的物理参数有:橡胶主簧的刚度( Kr ),橡胶主簧的等效活塞面积( Ap ),上液室的体积刚度( K1 ),惯性通道中液体的质量惯性系数( I i )和流量阻尼系数( Ri );而质量惯性系数又与惯性通道的尺寸参数和液体的比重有关,流量阻尼系数与液体的粘度、惯性通道的尺寸和形状等有关。由于橡胶主簧的阻尼系数很小,对液阻悬置性能的影响可以忽略不计,因此可以令Br = 0 。令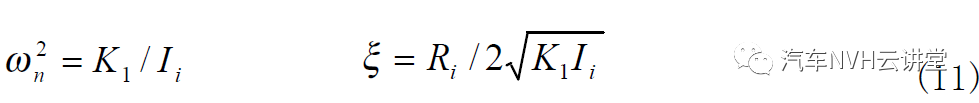
则惯性通道式液阻悬置的复刚度的计算公式(7)可以写成如下的形式:
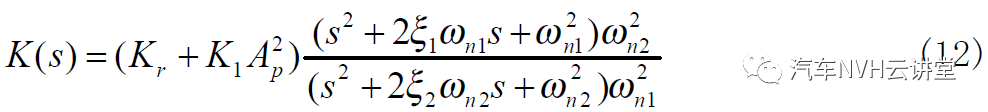
图 为惯性通道式液阻悬置的动刚度和滞后角的实验曲线,其中参数 f n1 (= ωn1 / 2π) 、f n 2 (= ωn 2 / 2π ) 是利用表 1 中的公式计算的到的。从图中可以看出,滞后角出现峰值的频率 f * 在 fn1 (ωn1 / 2π) 和 f n 2(ωn 2 / 2π) 之间,此公式揭示了体积刚度、橡胶主簧的刚度和惯性通道的尺寸参数与滞后角出现峰值频率的之间的关系。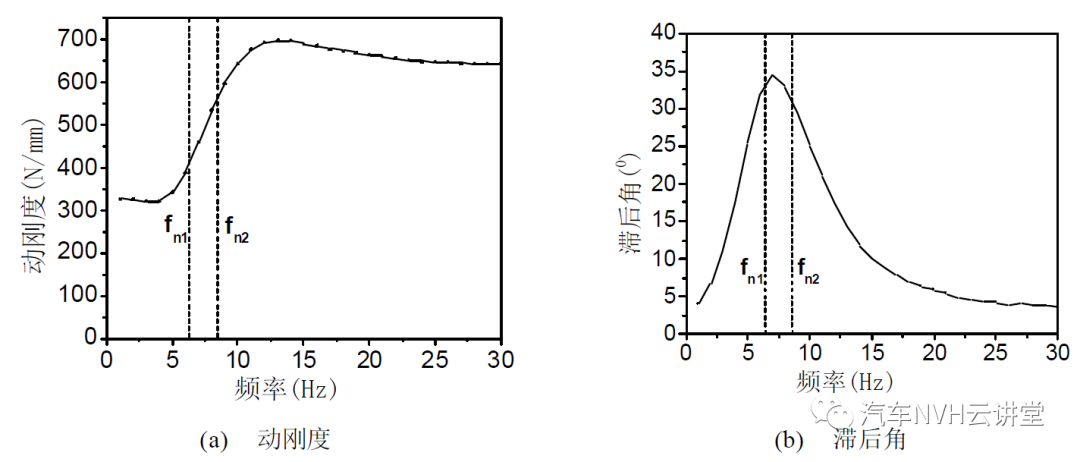
2.1 集总参数模型中物理参数的变化对液阻悬置动态特性的影响
假定当集总参数模型中的某一物理参数变化时,其它物理参数的值不变,讨论集总参数模型中物理参数的变化对液阻悬置的动刚度( Kd ),滞后角(φ),阻尼系数( C )和滞后角出现峰值时的频率( f Max )的影响规律。大量的计算和实验结果表明,橡胶主簧的阻尼 Br 对液阻悬置动刚度和滞后角的影响可以忽略不计,因此在设计液阻悬置时,不用考虑橡胶主簧的阻尼对液阻悬置性能的影响。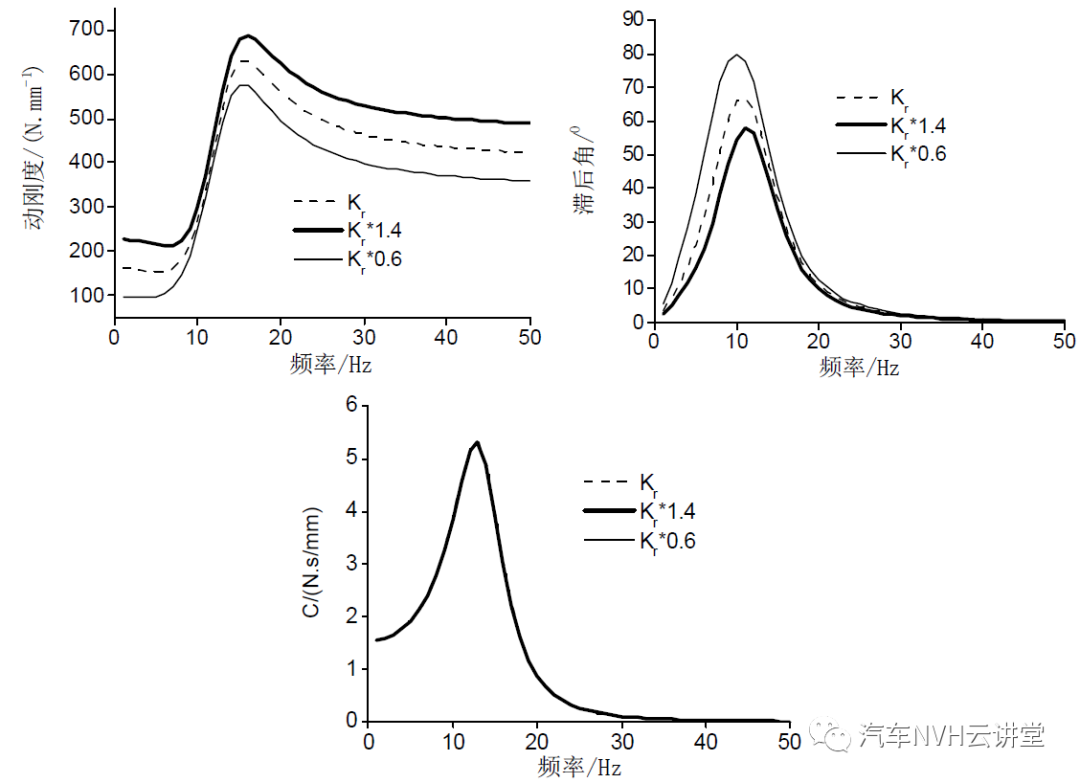
由3图可见,增加橡胶主簧的刚度,液阻悬置的动刚度增加而滞后角减少,滞后角出现峰值的频率增加。橡胶主簧刚度的变化对液阻悬置的阻尼系数没有影响。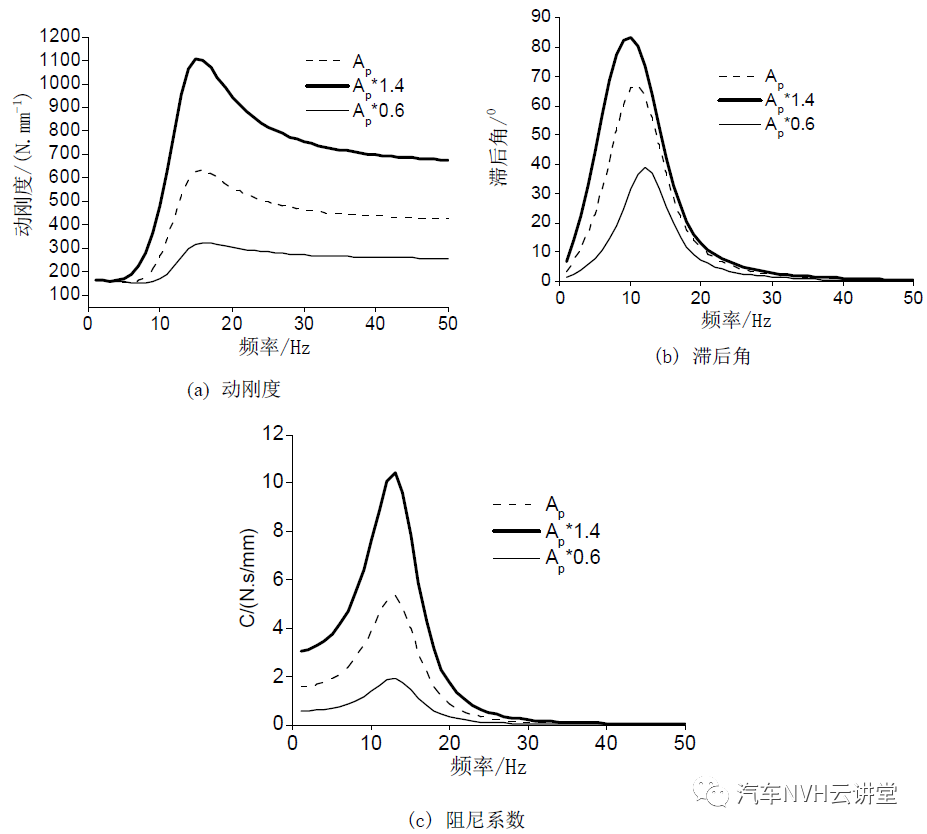
由 4 图可见,橡胶主簧的等效活塞面积增大时,液阻悬置的动刚度。滞后角和阻尼系数均增加,但滞后角出现峰值时的频率下降。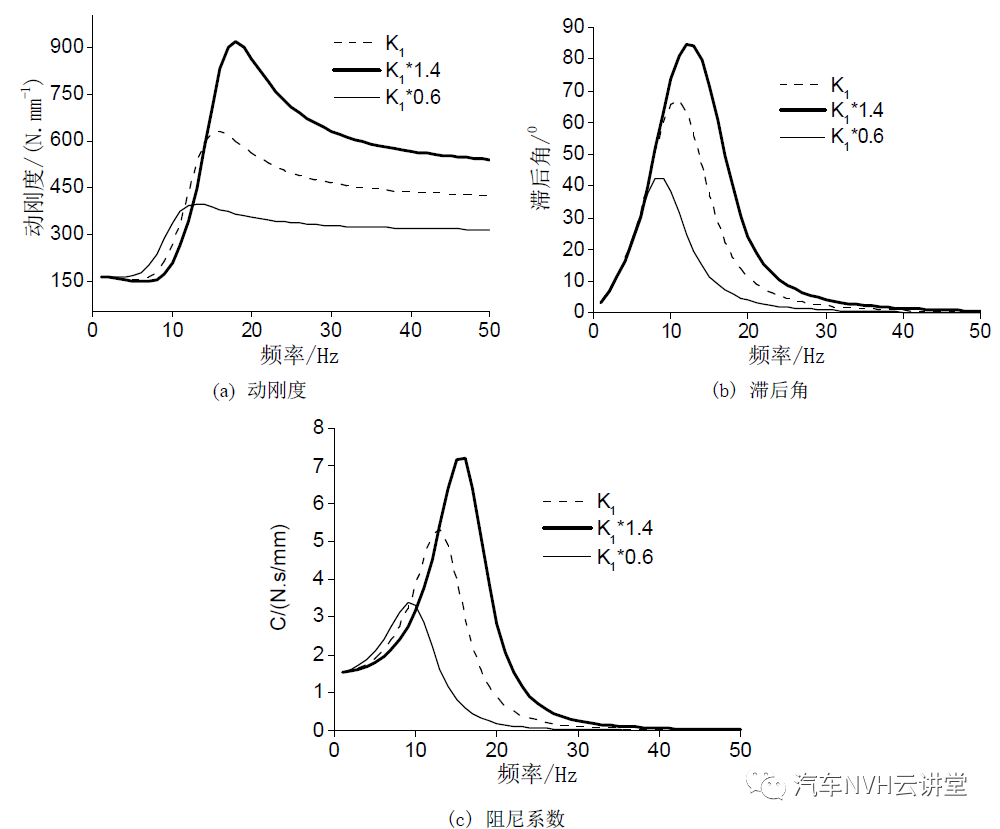
由 5 图可见,当上液室的体积刚度增加时,动刚度、滞后角和阻尼系数均增加,滞后角出现峰值时的频率也增加。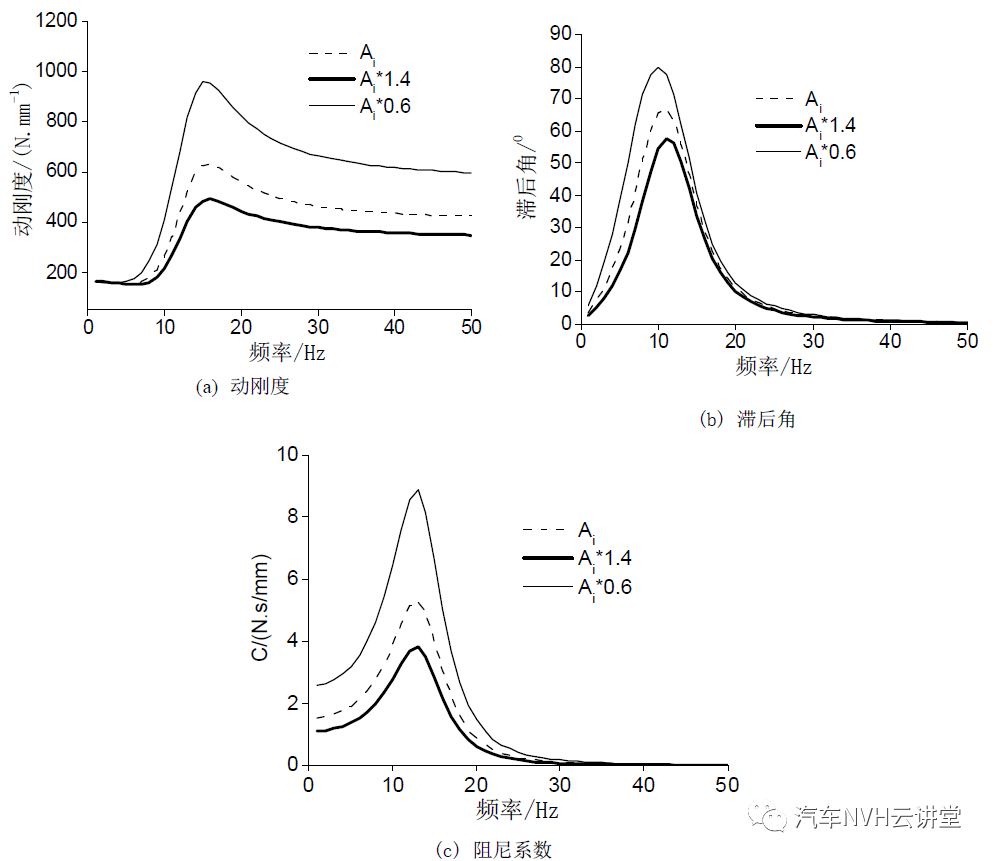
由 6 图可见,当惯性通道的横截面积增加时,动刚度、滞后角和阻尼系数均下降,当滞后角出现峰值时的频率增加。
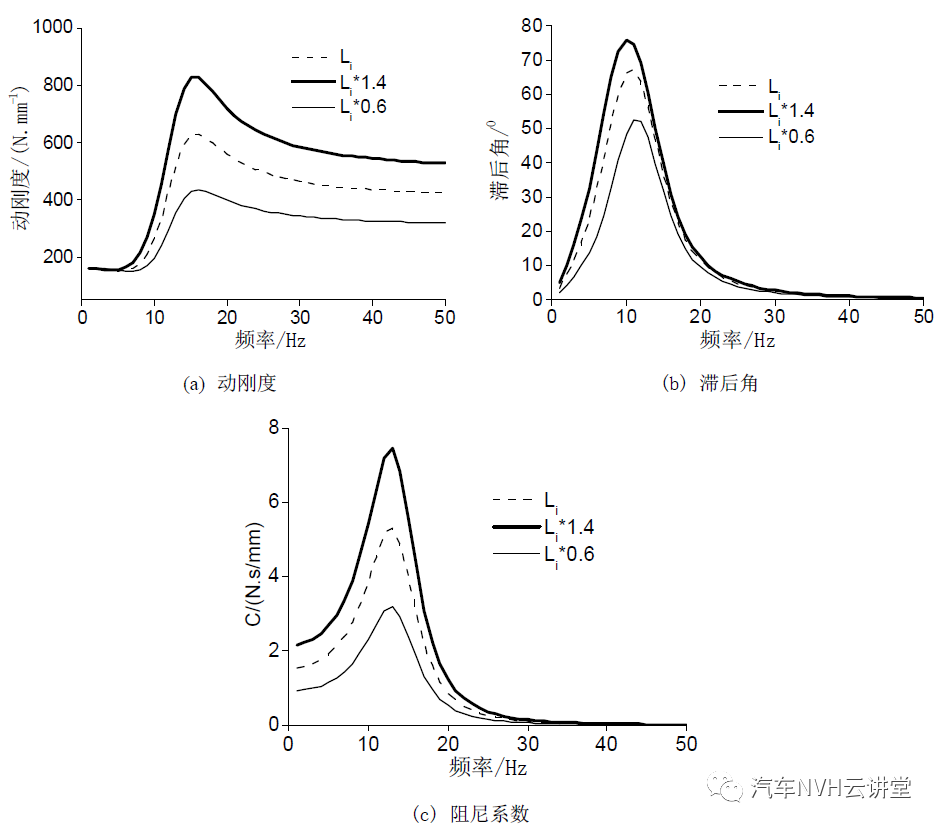
由图 7 可见,当惯性通道的长度增加时,动刚度、滞后角和阻尼系数均增加,滞后角出现峰值时的频率下降。对比图 和图 可见,惯性通道的长度对液阻悬置性能的影响与横截面积对液阻悬置性能影响的规律是相反的。
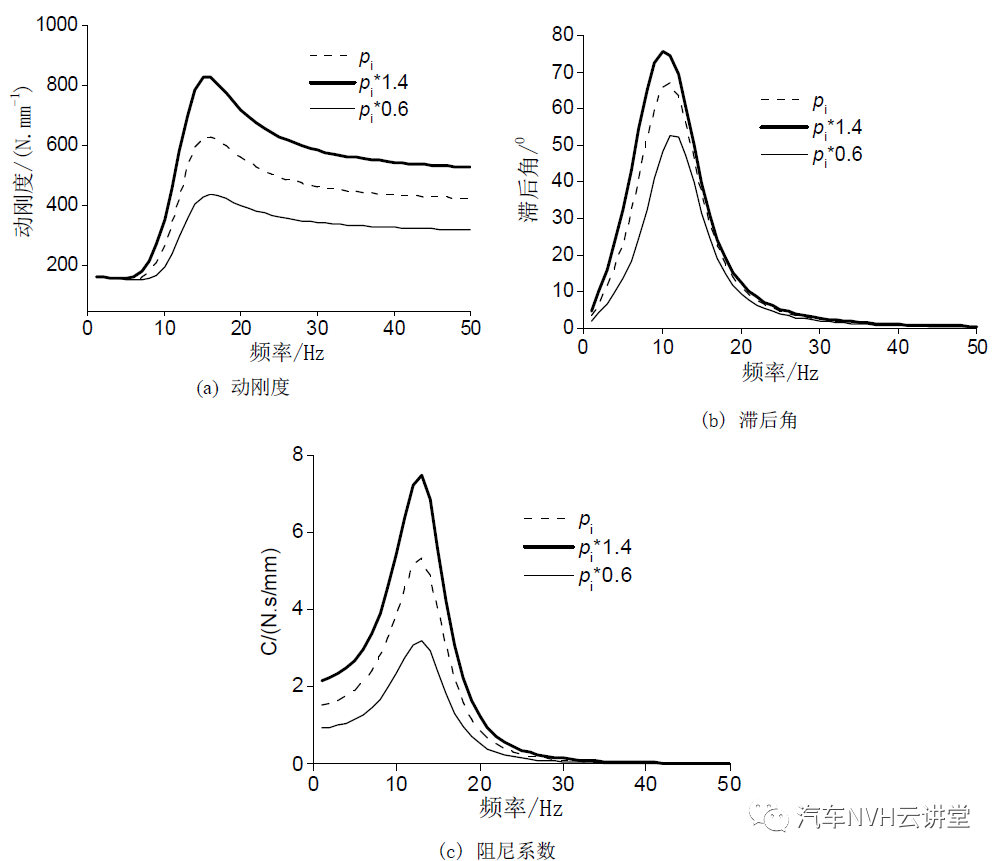
由图 8 可见,当液体的密度增加时,动刚度、滞后角和阻尼系数均增加,当滞后角出现峰值时的频率下降。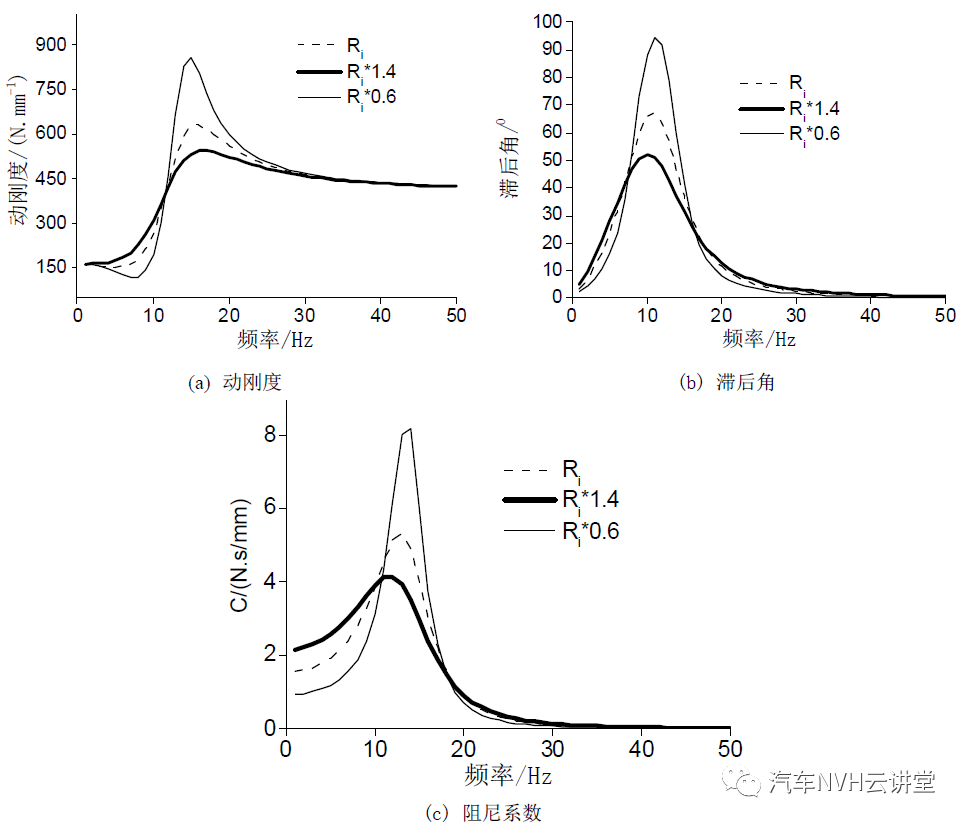
由图 9 可见,当流量阻尼系数增加时,动刚度、滞后角和阻尼系数均减少。流量系数的变化不影响滞后角出现峰值时的频率。综上所述,液阻悬置集总参数模型的物理参数对液阻悬置性能影响的一般规律如表2所示。表 2 集总参数模型物理参数的变化对液阻悬置性能的影响的一般规律
图14分别给出了惯性通道-解耦盘式液阻悬置(以下称液阻悬置 1)和惯性通道式液阻悬置(以下称液阻悬置 2)在低频、大振幅和高频、小振幅激励时动态特性的实测曲线。由图可见,两个液阻悬置在收到低频、大振幅激励时,两者的动刚度和滞后角曲线变化不大,因此,对惯性通道-解耦盘/解耦膜式液阻悬置的低频动特性分析时,不用考虑解耦盘/解耦膜对其动态特性的影响。当液阻悬置受到高频、小振幅激励时,在 150Hz 以下的频率范围内,液阻悬置 2 的动刚度大于液阻悬置 1 的,但是液阻悬置 1 的滞后角大于液阻悬置 2 的,并且在 100Hz 附近出现了较大的峰值,这是解耦盘及其互连液体的惯性所引起的。因此,在液阻悬置中引入解耦盘或者解耦膜,将使其动刚度在一定的频率范围减小,但其滞后角增加。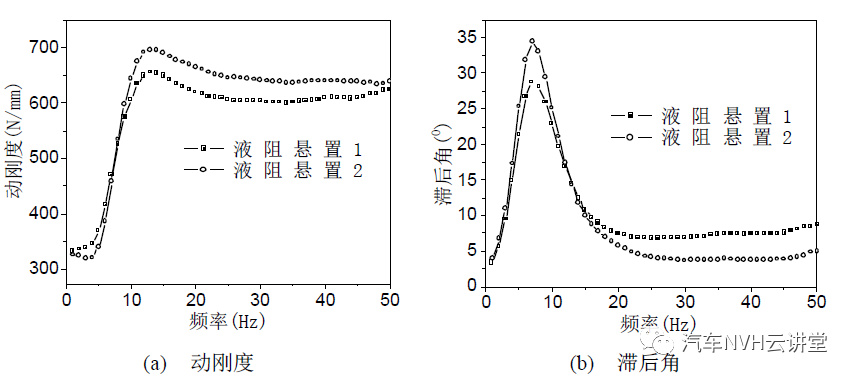
图 14 液阻悬置 1 和 2 的低频动态性能的比较
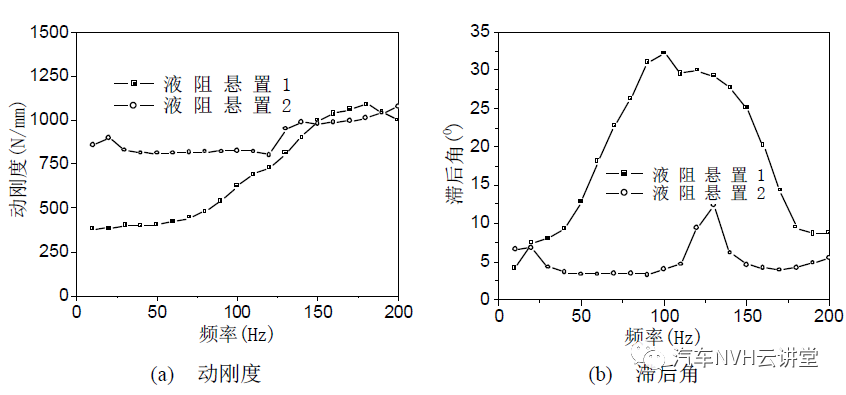
液阻悬置在一定振幅的激励下,由于其橡胶主簧类似于活塞,而使液体在上、下液室之间流动。当液阻悬置收到高频、小振幅激励时,为了使其在一定的频率范围内动刚度较小,而要求液体不流经惯性通道,在液阻悬置中引入解耦盘或者解耦膜结构,正是为了达到该目的。因此,解耦盘或者解耦膜能容如液体的容量是液阻悬置高频动态特性的一个重要考虑点。对解耦盘,其自由行程可由下式确定。
上式中, Ap 为橡胶主簧的等效活塞面积, Ad 为解耦盘的面积, xm 为激振振幅。在对液阻悬置的高频动态特性进行评价时,其激振振幅 xm 一般取 ± 0.1mm。
对于解耦膜,可容如的液体的体积与解耦膜的体积刚度有关,期望解耦膜所承受的压力和其体积刚度的变化曲线,如图 15所示。对解耦盘和解耦膜式两种解耦方式,一般认为解耦膜的引入对液阻悬置性能的改善有较大的好处,但解耦膜的设计、制造要比解耦盘的设计制造复杂。往期相关推荐
相关文章,在仿真秀官网搜索:
液压悬置气穴噪声(Cavitation Noise)影响因素及解决对策
利用三维有限元建模,通过迭代过程识别液压悬置的频率相关参数特性。 著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-13
最近编辑:2年前

 (1)
(1) (2)
(2)