田口鲁棒设计用于汽车动力总成悬置系统
关键词:悬置系统 田口鲁棒设计 隔振 鲁棒性优化
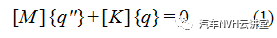
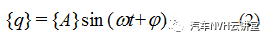
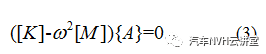
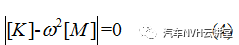
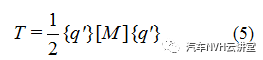

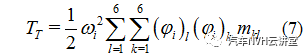



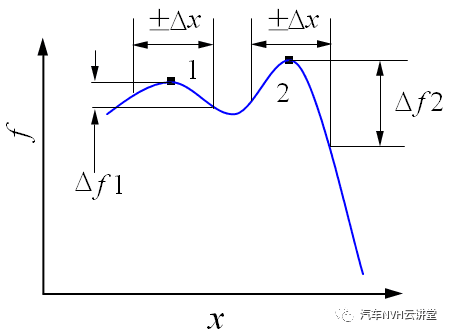
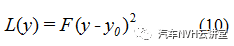
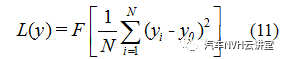
 (12)
(12)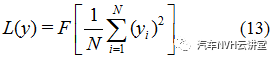
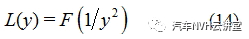

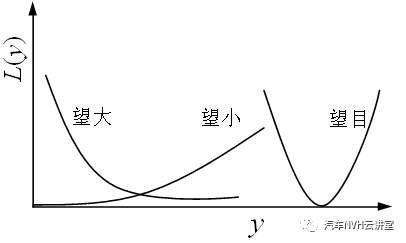

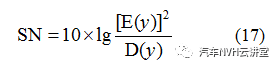











往期相关推荐
相关文章,在仿真秀官网搜索:
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-04-14
最近编辑:2年前
作者推荐
¥168
5.0
还没有评论
相关推荐
最新文章
热门文章
关键词:悬置系统 田口鲁棒设计 隔振 鲁棒性优化
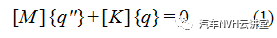
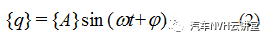
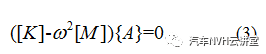
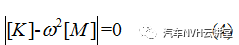
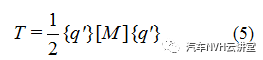

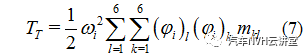




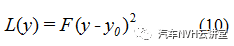
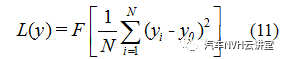
 (12)
(12)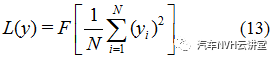
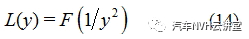















往期相关推荐
相关文章,在仿真秀官网搜索: