考虑安装误差的客车悬置系统的隔振研究

1年前浏览520

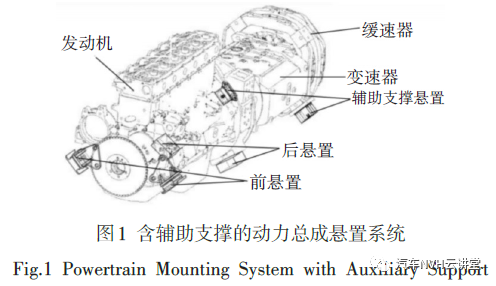
摘要：含辅助支撑客车动力总成悬置系统是一个超静定力学系统，安装误差可能导致系统振动恶化。通过建立客车动力总成悬置系统超静定力学物理模型，推导出相应的数学模型；通过MATLAB计算，对安装误差引起的悬置系统受力状态进行了分析；针对安装误差引起的悬置元件预载荷的变化，通过MTS台架对不同预载荷作用下悬置动刚度进行测试，对不同安装误差动力总成悬置系统固有频率和解耦率进行了分析，结果表明安装误差一定程度上使固有频率和解耦率偏离设计值；为减小安装误差对悬置系统影响，提出了辅助支撑悬置刚度设计的参考计算方法。

关键词：动力总成悬置系统；振动；辅助支撑；安装误差；客车；超静定

1 引言

汽车动力总成通过悬置元件安装在车架上，构成动力总成悬置系统。悬置系统的设计要满足对动力总成的支撑和限位作用，还要尽可能隔离发动机振动向车身传递和路面冲击传到动力总成。

客车发动机多数采用后置后驱、纵向布置，动力总成悬置元件通常以气缸中心线对称布置。在大中型客车上，变速器末端还安装有缓速器，用于辅助制动。安装缓速器后，整个动力总成长度较大，为减小动力总成内部的弯矩应力，通常在前悬置和后悬置的基础上，在缓速器位置布置辅助支撑悬置，构成五点或六点悬置系统，如图1所示。

含辅助支撑的动力总成悬置系统，从动力总成侧面看，是一个三点支撑的过定位系统，与无辅助支撑相比演变成超静定力学问题。若前悬置、后悬置和辅助支撑悬置在安装过程中存在误差，车辆静态时悬置元件存在内部应力。这间接使得动力总成内部存在应力，同时各悬置元件受到非常规预载荷作用，各悬置的动刚度与设计值出现较大偏离，悬置系统振动耦合加剧，悬置系统隔振性能变差，动力总成振动恶化。有不少学者针对客车动力总成悬置系统振动及隔振设计展开研究，而针对含辅助支撑的悬置系统存在的问题目前尚未见文献报道相关研究[1-4]。

2 动力总成悬置系统静态力学分析

2.1 不考虑安装误差的系统力学模型

以某款大巴典型的动力总成悬置系统为研究对象，两前悬置位于发动机前端，两后悬置位移飞轮壳下部，两辅助支撑位于缓速器下面。前悬置、后悬置和辅助支撑均与发动机汽缸中心线所在平面为对称面布置，所有悬置均为橡胶悬置。

将动力总成悬置系统进行必要的抽象简化以便建立数学模型。悬置元件的质量远远小于动力总成的质量，忽略不计[5]；发动机的安装倾角较小，假设发动机是以水平安装；动力总成的一阶弹性体模态频率远大于悬置系统刚体模态频率，假设动力总成为刚体[6]。悬置元件对称布置，从动力总成悬置系统的侧面看，可以将系统简化成一个三点支撑的平面力学模型，如图2所示。图中：F1—前悬置支撑力；F2—后悬置支撑力；F3—辅助支撑力；O—质心位置；G—系统重力；L1、L2和L3—前悬置、后悬置和辅助支撑到动力总成质心的距离。

Fig.2 Plane Mechanics Model of Powertrain Mounting System

根据力和力矩的平衡原理，有如下关系：

F1 + F2 + F3 = G （1）

F1 L1 = F2 L2 + F3 L3 （2）

动力总成同一平面受到三个力的作用，属于超静定力学问题。依据平衡方程（1）（2）尚无法求解各悬置点的受力状态。动力总成为刚体，悬置元件的变形和力之间存在一定的关系。假设安装没有误差，即动力总成吊装下落过程中，与前悬置、后悬置和辅助支撑悬置元件刚好接触；稳定落下后，由于悬置元件刚度的差异，各悬置变形也不一样，悬置元件在发动机长度方向的剪切变形非常小，忽略不计，如图3所示。图中虚线部分表示动力总成刚好与悬置元件接触时的位置，实线部分表示受力稳定后的位置。

在动力总成静止状态，假设前悬置、后悬置和辅助支撑悬置的变形量分别为a、b和c，则根据相似三角形定理，可得：

各悬置的变形量为：

式中：k1、k2和k3—前悬置、后悬置和辅助支撑在竖直方向上的刚度。根据式（1）～式（6），得到前悬置、后悬置和辅助支撑在竖直方向的受力为：

根据式（7）～式（9）可知，在悬置点安装位置确定的情况下，各悬置所受的力由各悬置的刚度共同决定。以辅助支撑刚度为横坐标，各悬置受力为纵坐标，通过MATLAB编写程序计算，得到各悬置受力随辅助支撑刚度变化的曲线，如图4所示。悬置系统设计过程中，可以通过辅助支撑的刚度选择对前悬置和后悬置的受力情况进行调整。

2.2 考虑安装误差的系统力学模型

在实际中，悬置支架加工制作有一定误差，车架也有一定的变形，在动力总成的安装过程中，动力总成落下时不能按设计的理想状态与三个悬置点同时接触。假设动力总成刚好与前后悬置元件接触时，辅助支撑悬置元件已变形Δx，Δx 可以是正值，也可以是负值。动力总成悬置系统元件的变形情况，如图5所示。根据相似三角形的定理，可得：

联合式（1）、式（2）、式（4）、式（5）、式（6）、式（10），可得各悬置受力与安装误差Δx之间的关系：

式中：i=1，2，3—前悬置，后悬置和辅助支撑。

2.3 安装误差对悬置系统的力学影响

由于安装误差的影响，在静止状态下，悬置系统在前悬置、后悬置和辅助支撑悬置的支撑受力不均匀，动力总成类似于跷跷板。为研究安装误差对系统受力状况的影响，根据前述选取的研究车型数据，取安装误差Δx在区间［-5，5］之间变化，在MATLAB求解方程组，计算出各悬置点受到的垂向力和安装误差之间的关系，如图6所示。

图6中，误差0mm是理想的设计状态，由图可见随着误差的增加，各悬置点的垂向受力也逐渐增大。各误差点与0点的值会在动力总成内部形成内应力，对动力总成造成不利影响。在±2mm误差区间内，前悬置载荷的变化为9.0%；后悬置载荷的变化为13.7%。

3 悬置系统振动特性分析

3.1 动力总成悬置系统振动模型

从三维空间的角度出发，按上文中的假设简化，同时橡胶悬置元件简化成具有三向主轴的弹性元件[7]，将动力总成悬置系统抽象成一个六自由度的振动模型[8]，如图7所示。根据所研究的车型有（1～6）个悬置元件，1和2为前悬置；3和4为后悬置；5和6为辅助支撑悬置。o2-u2v2w2为悬置元件2的坐标系，u2、v2、w2与悬置元件3个弹性主轴同向，每个悬置元件有各自坐标系，图示中为了图片清晰，仅标注悬置2的坐标。

定义质心坐标系O-XYZ，原点O 在质心位置，X 轴与曲轴中心线平行，指向曲轴皮带轮端；Z轴与气缸中心线平行，指向汽缸盖方向；Y轴根据右手定则确定。动力总成的振动分别为沿着定坐标系X、Y、Z 轴平动的x、y、z 和绕X、Y、Z 转动的θx，θy，θz，定义动力总成的广义坐标系：

根据振动理论建立动力学方程：

式中：x—系统广义坐标；［M］—系统质量矩阵；［K］—系统刚度矩

阵；［C］—系统阻尼矩阵；F—系统广义力矩阵。

3.2 动力总成悬置系统固有特性分析

求解系统固有振动频率时，不考虑阻尼，无阻尼自由振动微分方程为：

矩阵[M]-1[K]的特征值即为系统的圆频率；多自由度振动耦合率采用能量比表示时，当系统以第j 阶模态振动时，主振动方向（第k 个广义坐标）分配到的能量占系统总能量的百分比EPjk为[9]：

式中：（KEk）ωj—主振动方向能量；（KE）ωj—各自由度总能量。

根据所研究车型的参数，在MATLAB编写计算程序并求解，

得到系统的固有频率和解耦率，如表1所示。

由表1可见，动力总成悬置系统各阶振动频率在区间[5，17]Hz内，处于合理的范围[10]，各阶主振动方向的振动解耦率也较高，系统有较好的振动特性。

4 安装误差对系统隔振特性影响

4.1 橡胶悬置动刚度力学特性

悬置系统工作处于动态载荷的环境下，在动力总成悬置系统固有特性的计算中，刚度矩阵［K］由各悬置元件3个方向主轴的动刚度构成。动刚度是弹性体抵抗动态载荷的能力。橡胶悬置元件动刚度主要影响因素有预载荷、振幅、频率和温度，通常橡胶制品的动刚度与预载荷、频率呈正相关，与振幅的大小呈负相关[11]。在动力总成固有特性的计算参数，根据具体动力总成工况选取测试条件。

根据研究对象，在室温状态下，使用MTS弹性体动静刚度试验台架，分别测试同一频率（10Hz）、同一振幅（±2mm），不同预载荷状态下的动刚度，前悬置、后悬置和辅助支撑悬置的动刚度如图8所示。测试时选取测试区间内均匀分布的几个点，采用曲线拟合的方法可以得到任意预载荷加载下的悬置元件动刚度。由图可见，各悬置元件动刚度随着预载荷的增加有较大增加。

4.2 误差对悬置系统振动响应分析

由前文的分析可知，前悬置、后悬置和辅助支撑受安装误差影响，各悬置垂向力的有较大变化。动力总成静态下悬置元件载荷即为悬置元件动刚度测试时的预载荷，安装误差间接的引起了悬置元件动刚度的变化。根据前文结论，不同安装误差各悬置元件有不同的预载荷，再根据前文测试的数据，在拟合的曲线上可以得到相应的动刚度。通过编程求解得到动力总成悬置系统固有频率和解耦率随误差变化曲线，如图9、图10所示。

由图9可见，在x，y，θy和θz方向频率变化不大，在z 和θx方向振动频率有一定的变化，而这两方向是动力总成主要的振动方向，也是隔振设计重点关注的方向，安装误差会使得系统实际固有频率与设计值出现偏差，系统振动恶化等情况。

由图10可见，在y 方向和z 方向，动力总成悬置系统的解耦率随着安装误差的变化而变化，在安装误差Δx为负值时，解耦率有明显的下降，这会使得系统在主要振动方向z隔振率变差。

4.3 辅助支撑刚度设计要求

由前面的分析可知，含辅助支撑的动力总成悬置系统，安装误差会给动力总成带来内部应力，同时给系统隔振性能带来诸多不利的影响。这些影响本质上是由于误差引起的载荷变化造成的，且各悬置载荷的变化与辅助支撑的刚度相关，因此辅助支撑悬置刚度的选择尤为重要。刚度选择过小，辅助支撑起到的支撑作用有限，刚度选择过大，安装误差会使动力总成内应力和悬置系统的隔振性能变差。

为减小安装误差对系统造成的影响，辅助支撑的刚度必须满足一定条件，假设安装误差在±2mm内，前后悬置垂向载荷的变化要小于±10%，运用数学表达有如下关系：