汽车电驱动系统由电机、减速器、控制器等部件构成,其主动噪声源包括机械噪声以及电磁噪声。其中机械噪声由减速器激励、轴承激励、转子偏心激励引起;电磁噪声主要由气隙磁密产生的旋转力波,作用在定子铁心上,引起结构振动进而向外辐射噪声。
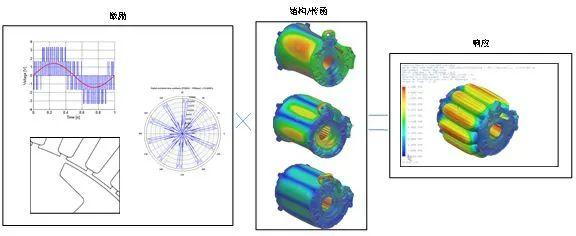
在对电驱动系统进行仿真分析时,通常分为:载荷提取;结构有限元建模;振动响应计算;噪声计算四个环节,其基本原理可由下图简要表示:
提取电磁力的常见方法有虚功 法与麦克斯韦张量法,虚功 法计算原理相对复杂,但其能够相对准确提取电磁力,且对网格不敏感;同时能够考虑磁饱和、几何突变等因素下的电磁力;麦克斯韦张量法计算过程相对简单,数据便于编程处理及与其它软件耦合计算,但网格敏感性较高,且计算精度依赖于积分路径的选择。 由上式可知,麦克斯韦压力是空间角度和时间的函数。因而,在提取气隙或者齿面麦克斯韦压力时,得到的是关于空间角度和时间的二维数据。 那么,对磁密数据进行二维傅里叶变换,将得到电磁力的空间与频率阶次。当径向电磁力的空间阶次和频率分别同时等于电机定子圆柱模态轴向阶次和频率时,才会导致定子结构共振。此外,电机电磁振动噪声水平近似与径向力空间阶次的四次方成反比,径向力空间阶次越高,对电磁振动噪声的影响越小。 但如章节一所述,麦克斯韦张量法计算电磁力的精度对网格敏感程度高,且计算精度依赖于积分路径的选择,因而在进行电磁力计算时需要格外注意。同时,进行电磁力映射时,需要格外注意离散数值积分的积分精度以及积分路径的选择。已有大量数据表明,槽口处麦克思维压力的映射方法将对计算结果,尤其是切向激励产生显著影响。 
总成有限元建模是振动噪声计算最基础也是最关键的环节之一。有限元模型直接决定了振动噪声计算结果的准确性和计算效率。其中,两个重要环节分别是,铁心正交各向异性材料参数的获取,以及绕组的简化形式。 
图6 总成有限元模型示意
铁心的材料参数获取方式主要有两种,借助模态测试结果对仿真结果进行校准;建立周期单元,仿真计算叠压材料的等效参数。 有模型修正方法可分为两大类:一是修正结构的有限元系统矩阵,修正对象为质量、刚度等物理矩阵,也称为矩阵型修正方法;二是直接修正结构的设计参数,如密度、杨氏模量等。模型修正的思想为:以实测模态参数和有限元模型作为参考基础,寻找满足特征方程、正交性条件、对称性条件或关联性条件等,且与参考基础最接近的计算模型。基于这个基本思路,在各种不同的假设下,发展了很多修正方法。 
图7 圆柱对不同参数的灵敏度
另外一种方法则是建立下图周期单元,计算其在不同方向的拉伸与纯剪切作用的应力应变,进而得到其等效弹性模型、剪切模量与泊松比。

图8 仿真方法参数识别原理
通常,无论借助仿真还是模态测试结果,均能获得相对理想的参数结果。

图9 模型校准结果
需要关注的是,铁心模态测试通常是在常温下进行的,但电机在实际运行中铁心问题可高达~60~70℃。高温下铁心的材料属性,尤其是阻尼将发生显著变化。因而,在仿真计算时需要格外注意。 绕组等效方式多种多样,比如保留有效绕组,忽略端部绕组;保留有效绕组,将端部绕组等效为圆环;保留等效绕组,端部绕组等效为质量点;省略绕组,将绕组对铁心刚度、质量的贡献等效在定子齿部等等。总的来说,并没有统一的等效方式确定绕组简化方式,而是要根据实际绕组形式或者模态测试结果,尝试相对合理的简化方式。 但需要注意的是,无论使用哪种等效方式,绕组的等效模量通常远低于铜的模量。如简化不合理,那么绕组将出现大量的高阶模态,使模态数量急剧上升。模态数量的上升一方面导致计算时间大大增加,另一方面讲有可能导致模态叠加法得到的计算结果出现异常。另外,如果将绕组对铁心刚度、质量的贡献等效在定子齿部,那么定子齿有可能在高频段出现大量的弯曲的模态,在进行计算时也需要重点关注。 
图10 齿根弯曲模态
总成振动响应计算完成后,可使用有限元或者边界元方法计算其辐射噪声。通常,声学计算是相对比较耗时的过程。一方面,声学建模时,为了满足每个波长内六个节点的要求,通常计算频率越高,声学网格尺寸越小,对应的声学网格数量越大;另一方面,声学计算是以结构的振动速度作为边界条件进行声传播计算。振动响应计算过程中,如果存储总成结构有限元模型中每个节点上的振动位移或速度信息,结果文件会异常巨大。一方面增大了振动响应的计算时间,另一方面,进行声传播计算时,声学软件读取振动结果存储文件,也将是一个漫长的过程。 由声学基本原理可知,辐射声功率与结构表面振动速度存在如下关系: 
因而,总成振动响应计算完成后,通过提取表面振动速度均方值,并使用声辐射系数进行修正,进而得到其声功率结果。

图11 声辐射系数示意
复杂结构准确的声辐射系数通常难以通过解析计算或者,这也正是有限元或者边界元声学软件计算噪声的意义所在。幸运的是,声辐射系数在高频段近似等于1,而我们关注的电驱动系统噪声通常在高频段。认为,认为修正声辐射系数得到的声功率结果是可靠的。借助这种方法,可将整个加速区间不同阶次的噪声计算时长缩短到1小时内。

图12 噪声计算结果
电驱动系统噪声计算是一个计算路径相对较长,计算过程涉及电磁计算、载荷插值、结构计算、声传播计算几个过程。长路径计算往往意味着误差累计,因而容易导致计算结果与实际结果严重偏离。同时,电驱电磁噪声计算过程中做了大量的简化与假设,例如,忽略磁饱和效应在铁心内部节点产生的电磁力;人为选取简易积分路径代替铁心与空气交界面实际积分路径;有限精度的离散数值积分与载荷映射;简化工艺误差对磁场的影响;强耦合过程简化为弱耦合;声辐射系数近似等等。 一系列简化与假设极容易导致计算结果可信度不高。应验了学术圈的那句名言:对于实验数据,通常是除了自己不相信,其它人都相信;对于仿真数据,则是除了自己相信,其它人都不信。 但从另一方面来说,任何一款工业软件都是无数工程师心血的结晶。仿真方法是好的,但也只有认清问题的本质,了解各个工具的边界,并结合实际面临的问题去选择合适、合理的路径,才能真正起到指导设计或者解决问题的作用。