力学仿真笔记——五种常见的屈服准则及其优缺点、适用范围
屈服准则表示在复杂应力状态下材料开始进入屈服的条件,它的作用是控制塑性变形的开始阶段。屈服条件在主应力空间中为屈服方程。
五种常用的屈服准则,它们分别是Tresca准则,Von-Mises准则 ,Mnhr-Coulomb准则,Drucker Prager准则,Zienkiewicz-Pande准则。其中后三种适用于混凝土和岩土材料的准则。
1. Tresca屈服准则
当最大剪应力达到一定数值时,材料开始屈服。这就是Tresca屈服条件,也称为最大剪应力条件。

规定σ1≥σ2≥σ3时,上式可表示为:

如果不知道σ1、σ2、σ3的大小顺序,则屈服条件可写为:
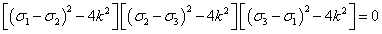
换言之当变形体或质点中的最大切应力达到某一定值时,材料就发生屈服。或者说,材料处于塑性状态时,其最大切应力是一个不变的定值,该定值只取决于材料在变形条件下的性质,而与应力状态无关。所以Tresca屈服准则又称为最大切应力不变条件。
这种模型与静水压力无关,也不考虑中间应力的影响。在平面上屈服条件为一个正六边形,在主应力空间内,屈服曲面为一个正六面柱体。
Tresca屈服准则不足之处就是不包含中间主应力,没有反映中间主应力对材料屈服的影响。
2. Mises屈服准则
当与物体中的一点应力状态对应的畸变能达到某一极限值时,该点便产生屈服,其表达式为:

或
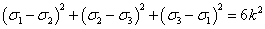
其中, k为常数,可根据简单拉伸试验求得:
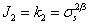
或根据纯剪切试验来确定:

它所代表的屈服面是一个以空间对角线为轴的圆柱体,在平面上屈服条件是一个圆。这时有:
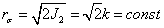
换言之当等效应力达到定值时,材料质点发生屈服,该定值与应力状态无关。或者说,材料处于塑性状态时,其等效应力是不变的定值,该定值取决于材料变形时的性质,而与应力状态无关。Mises屈服准则的物理意义:当材料的单位体积形状改变的弹性能达到某一常数时,质点就发生屈服。故Mises屈服准则又称为能量准则。
3. Mnhr Coulomb准则
Tresca屈服条件和Mises屈服条件主要是对金属材料成立的两个屈服条件,但是这两个屈服条件如果简单地应用于岩土材料,会引起不可忽视的偏差。
针对此,Mohr提出这样一个假设:当材料某个平面上的剪应力τn达到某个极限值时,材料发生屈服。这也是一种剪应力屈服条件,但是与Tresca屈服条件不同,Mohr假设的这个极限值不是一个常数值,而是与该平面上的正应力σn有关,它可以表示为:

上式中,C是材料粘聚强度,Φ是材料的内摩擦角。这个函数关系式可以通过实验确定。一般情况下,材料的内摩擦角随着静水应力的增加而逐渐减小,因而假定函数对应的曲线在σn-τn平面上呈双曲线或抛物线或摆线。但在静水应力不大的情况下,屈服曲线常用Φ等于常数的直线来代替,它可以表示为:
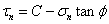
上式就称为Mohr—Coulomb屈服条件。
设主应力大小次序为σ1≥σ2≥σ3,则上式可以写成用主应力表示的形式
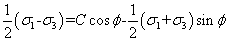
4. Drucker Prager准则
Drucker-prager屈服准则是对Mohr-Coulomb准则的近似,它修正了Von Mises 屈服准则,即在Von Mises表达式中包含一个附加项。其屈服面并不随着材料的逐渐屈服而改变,因此没有强化准则, 塑性行为被假定为理想弹塑性,然而其屈服强度随着侧限压力(静水应力)的增加而相应增加,另外,这种材料考虑了由于屈服而引起的体积膨胀,但不考虑温度变化的影响。故此材料适用于混凝土、岩石和土壤等颗粒状材料。
在主应力空间中,D-P屈服面为一曲面,其表达式为:
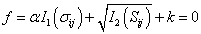
上式:f为塑性势函数,I1(σij)为应力张量第一不变量,I2(Sij)为应力偏张量第二不变量,α,k为材料常数,是材料c,φ的函数,c,φ分别为材料的粘聚力和内摩擦角。
5. Zienkiewicz-Pande准则
Zienkiewicz-Pande 屈服准则是 Mohr-Coulomb 准则的改进,在 p-q 子午面和 π 平面上都是光滑曲线,不存在尖点,在数值迭代计算过程中易于处理,而且在一定程度上考虑了屈服曲线与静水压力的关系以及中主应力σ。是由Zienkiewicz、Pande 等学者在1977 年对 M-C 准则进行了修正与推广时,形成了具有 3 种曲线形式的 Zienkiewicz-Pande 准则(简称 Z-P 准则)。这主要是考虑到M-C 准则在角点处存在奇异性,即其屈服曲线在 π 平面上有尖点,使得计算过程中出现奇异,特别在有限元迭代过程中,在尖角处无法处理的问题。
1. Tresca准则
优点:当知道主应力的大小顺序,应用简单方便。
缺点:
(1) 没有考虑正应力和静水压力对屈服的影响;
(2) 屈服面有转折点,棱角,不连续。
适用:金属材料
2. Mises屈服准则
优点:
(1) 考虑了中主应力σ²对屈服和破坏的影响;
(2) 简单实用,材料参数少,易于实验测定;
(3) 屈服曲面光滑,没有棱角,利于塑性应变增量方向的确定和数值计算。
缺点:
(1) 没有考虑静水压力对屈服的影响;
(2) 没有考虑单纯静水压力p对岩土类材料屈服的影响及屈服与破坏的非线性特性;
(3) 没有考虑岩土类材料在偏平面上拉压强度不同的S-D效应。
适用:金属材料
3. Mohr-Coulomb屈服准则
优点:
(1) 反映岩土类材料的抗压强度不同的S-D效应对正应力的敏感性;
(2) 反映了静水压力三向等压的影响;
(3) 简单实用,参数简单易测。
缺点:
(1) 没有反映中主应力σ²对屈服和破坏的影响;
(2) 没有考虑单纯静水压力引起的岩土屈服的特性;
(3) 屈服面有转折点,棱角,不连续,不便于塑性应变增量的计算。
适用范围:岩石、土和混凝土材料
4. Drucker-Prager屈服准则
优点:
(1) 考虑了中主应力σ²对屈服和破坏的影响;
(2) 简单实用,材料参数少,可以由C-M准则材料常数换算;
(3) 屈服曲面光滑,没有棱角,利于塑性应变增量方向的确定和数值计算;
(4) 考虑了静水压力对屈服的影响;
(5) 更符合实际。
缺点:
(1) 没有考虑单纯静水压力p对岩土类材料屈服的影响及屈服与破坏的非线性特性;
(2) 没有考虑岩土类材料在偏平面上拉压强度不同的S-D效应;
适用范围:岩石、土和混凝土材料
5. Zienkiewice-Pande准则
优点:
(1) 三种曲线在子午面上都是光滑曲线,利于数值计算;
(2) 在一定程度上考虑了屈服曲线与静水压力的非线性关系;
(3) 在一定程度上考虑了中主应力σ²对屈服和破坏的影响。
适用范围:岩石、土和混凝土材料

专注共享CAE仿真软件的安装包、安装破解汉化教程、免费学习教程和技术资料、操作技巧、工程案例以及专业模拟仿真技术等。更多精彩欢迎持续关注***:CAE仿真学社,时刻学习掌握CAE模拟仿真技术!有任何问题、需求请联系我们,有朋友就有未来!
祝您工作、学习和生活愉快!
 精彩无限
精彩无限


欢迎点赞、关注、转发、分享、交流




