仿真笔记——流体网格为什么有边界层划分
边界层是高雷诺数绕流中紧贴物面的粘性力不可忽略的流动薄层,又称流动边界层、附面层。这个概念由近代流体力学的奠基人,德国人Ludwig Prandtl(普朗特)于1904年首先提出。从那时起,边界层研究就成为流体力学中的一个重要课题和领域。

十九世纪末叶,流体力学这门科学开始沿着两个方向发展,而这两个方向实际上毫无共同之处。一个方向是理论流体动力学,它是从无摩擦、无粘性流体的Euler运动方程出发发展起来的,并达到了高度完善的程度。然而,由于这种所谓经典流体动力学的结果与实验结果有明显的矛盾——尤其是关于管道和渠道中压力损失这个非常重要的问题,以及关于在流体中运动物体的阻力问题——这就是达朗伯佯谬。正因为这样,注重实际的工程师为了解决在技术迅速发展中所出现的重要问题,自行发展了一门高度经验性学科,即水力学。水力学以大量的实验数据为基础,而且在方法上和研究对象上都与理论流体动力学大不相同。
二十世纪初,L.Prandtl因解决了如何统一这两个背道而驰的流体动力学分支而著称于世。他建立了理论和实验之间的紧密联系,并为流体力学的异常成功的发展铺平了道路。就是在Prandtl之前,人们就已经认识到:在很多情形下,经典流体动力学的结果与试验结果不符,是由于该理论忽略了流体的摩擦的缘故。而且,人们早就知道了有摩擦流动的完整的运动方程 (Navier-Stokes方程)。但是,因为求解这些方程在数学上及其困难(少数特殊情况除外),所以从理论上处理粘性流体运动的道路受到了阻碍。此外,在两种最重要的流体,即水和空气中,由于粘性很小,一般说来,由粘性摩擦而产生的力远小于其它的力(重力和压力)。因为这个缘故,人们很难理解被经典理论所忽略的摩擦力怎么会在如此大的程度上影响流体的运动。
1904年,Heidelberg数学讨论会上宣读的论文“具有很小摩擦的流体运动”中,L.Prandtl指出:有可能精确地分析一些很重要的实际问题中所出现的粘性流动。借助于理论研究和几个简单的实验,他证明了绕固体的流动可以分成两个区域:
一是物体附近很薄的一层(边界层),其中摩擦起着主要的作用;
二是该层以外的其余区域,这里摩擦可以忽略不计。
基于这个假设,Prandtl成功地对粘性流动的重要意义给出了物理上透彻的解释,同时对相应的数学上的困难做了最大程度的简化。甚至在当时,这些理论上的论点就得到一些简单实验的支持,这些实验是在Prandtl亲手建造的水洞中做的。因此,他在重新统一理论和实践方面迈出了第一步。边界层理论在为发展流体动力学提供一个有效的工具方面证明是极其有成效的。自20世纪以来,在新近发展起来的空气动力学这门学科的推动下,边界层理论已经得到了迅速的发展。在一个很短的时间内,它与其他非常重要的进展(机翼理论和气体动力学)一起,已成为现代流体力学的基石之一。
如果粘性很小的流体(如水,空气等)在大雷诺数时与物体接触并有相对运动,则靠近物面的薄流体层因受粘性剪应力而使速度减小;紧贴物面的流体粘附在物面上,与物面的相对速度等于零;由物面向上,各层的违度逐渐增加,直到与自由流速相等。L-普朗特把从物面向上的这一流体减速薄层叫作边界层。

无攻角平行流沿平板的边界层示意图
由物面向外,流体速度迅速增大至当地自由流速度,即对应于理想绕流的速度,一般与来流速度同量级。因而边界层内速度的法向垂直表面的方向梯度很大,即使流体粘度不大,如空气、水等,粘性力相对于惯性力仍然很大,起着显著作用,因而属粘性流动。
而在边界层外,速度梯度很小,粘性力可以忽略,流动可视为无粘或理想流动。在高雷诺数下,边界层很薄,其厚度远小于沿流动方向的长度,根据尺度和速度变化率的量级比较,可将纳维-斯托克斯方程简化为边界层方程。求解高雷诺数绕流问题时,可把流动分为边界层内的粘性流动和边界层外的理想流动两部分,分别迭代求解。边界层有层流、湍流、混合流 ,低速(不可压缩)、高速(可压缩)以及二维、三维之分。由于粘性与热传导紧密相关,高速流动中除速度边界层外,还有温度边界层。
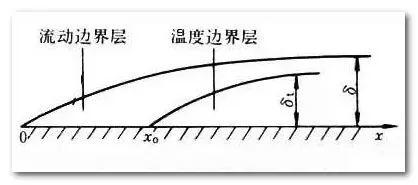
边界层内从物面 (当地速度为零)开始,沿法线方向至速度与当地自由流速度U 相等(严格地说是等于0.990或0.995U)的位置之间的距离,记为δ 。
边界层厚度与流动的雷诺数、自由流的状态、物面粗糙度、物面形状和延展范围都有关系。由绕流物体头部(前缘)起,边界层厚度从零开始沿流动方向逐渐增厚。当空气流的雷诺数为Rex=10时,在距前缘1米处,平板上层流边界层的厚度为3.5毫米。在平滑平板上,层流边界层的厚度。

流体绕物体流动时,在物体的前端或上游部分的边界层,一般是层流边界层。沿曲面的层流边界层。由于外流速度有变化,与平板有所不同,但速度分布大致类似。紧贴物面的速度梯度较大,因而剪应力也较大。物面上的剪应力为:
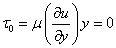
式中, 为流体动力粘性系数。算出了τ0,就可求出物面的摩擦阻力系数和摩擦阻力。但这些计算只能用于分离点以前。

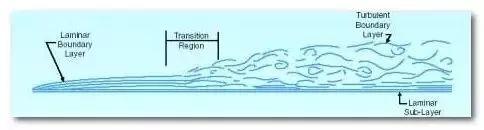
在自然界和工程中,运动物体(如飞机、叶栅等)表面上的流动大部分是湍流边界层。由于湍流是有涡流动,有随机的脉动,流动随空间和时间都在变化,所以湍流边界层的内部结构比层流边界层复杂得多。由于湍流内有垂直流向的动量交换,它在与壁面垂直截面上的速度分布与层流边界层的不同,下端丰满一些。
由实验数据,可把湍流边界层近似地看作由内区和外区组成。这样的分法,是因为靠近壁面的粘性剪应力与压力梯度在这两个区内是截然不同的。内区包括贴近壁面的粘性底层,其中剪应力最大,由许多小旋涡组成,向上是缓冲层,再向上直到边界层外区是大尺寸旋涡组成的动量交换较大的湍流层;外区是从这个湍流层一直到速度与外流极相近的地方。总的来说,内区占边界层全层的20%。

从湍流边界层的研究历史来看,存在着两种理论,它们分别发展又相互关联:一种是统计理论,另一种是半经验理论。
在统计理论中,把流体看做连续介质,把流速、压力等的脉动值看做连续的随机函数,通过各脉动值的相关函数和谱函数来描述湍流流动。按统计平均法,从中找出脉动结构,把各种平均值代入纳维—斯托克斯方程及其他方程,得出所谓雷诺方程。但统计理论主要用于研究均匀各向同性湍流,对湍流边界层流动并不适合。
在另一种半经验理论中,因为湍流边界层方程的数目少于未知量的数目,方程组是不封闭的,因而需要补充一些关系式。由此而产生的一些不严谨的近似理论为半经验理论,这些理论无严格的依据,但对解决工程上的许多问题很有用处。又因为其中有些系数是从实验中求出的,所以用这些半经验理论算出的结果,常与实验较吻合,但它们的适用范围有局阻性。常用的半经验理论有:J.V.布森涅斯克于1877年提出的,用涡粘性系数计算雷诺应力的公式,昔朗特的混合长理论(动量传递理论):G.I.泰勒的涡旋传递理论,卡门的相似理论等。这些半经验理论的缺点是对湍流的内部结构都没有做分析,使用范围有限。
流体流过曲面时,它的速度和压力都有变化。当流速减少时,压力必定增加。由于在边界层内的流体微团有动量损失,如遇到下游压力增加(即有逆压梯度)时,则动量再减少,直到流体微团不能再在物面上前进时就会从物面分离,这一现象叫做边界层分离。气流开始离开物面的点称为分离点。
在实验方面,测分离点位置可用模型表面的油流法、丝线法和用普雷斯顿管等。各国对分离流尤其是对二维非定常流和三维定常流中边界层分离的起始及分离点,线附近流动问题的研究愈益重视,已有一些近似理论如三层结构等,也试提出二维、三维流动的分离判据,研究正在不断深入中。
在应用上(例如对航空飞行器来说),层流边界层的过渡和分离,使机翼等阻力增加和(或)举力减少(甚至失速),因此人们很早就设法使机翼表面光滑,并设计“层流翼剖面”,以维持层流边界层。但这种控制是有限的,所以人们后来采用了许多人工控制边界层的方法,以达到影响边界层结构,从而避免边界层内气流分离,和减少阻力增加举力的目的。实验和理论得出如下的使流体局部加速的几种有效方法:
使部分物面移动;
通过物面上的喷孔(狭缝)吹出流体,以增加表面滞流的能量;
通过物面上的狭缝,吸走滞流,使边界层变薄,以抑制分离;
用不同气体喷射,加速滞流;
变更机翼形状。
在很多工程问题中,控制边界层脱离十分重要。控制边界层脱离的方法很多,但无外乎两大类:
一类是改变物体的形状,控制物面上的压强梯度,从而尽量缩小脱离区,例如采用细长的流线形物面;
另一类是考虑流动的内部因素,增加边界层内流体微团的动量以加强抗逆压力梯度的能力,如:在壁面吹吸流体,延缓分离,减少分离区,达到减少压差阻力的效果。由于流动的分离点和来流的状态有关,因此,在周定点处吹气或吸气的控制方法往往不能满足实际的要求。
近年来,利用微型传感器溅量绕流物面的流动特性(如压强或压强梯度),根据测得的信息,在物面必要的位置实行流动控制,这种带有反馈信息的控制方法称作主动控制。
来源:CAE仿真学社




