【JY】ETABS的非线性直接积分法的设置与应用
ETABS中有两种弹塑性时程分析方法,分别是非线性模态分析法(FNA法)和非线性直接积分法。其中FNA适合于带有少量非线性连接单元的结构,计算速度快是其主要优点,在减隔震分析中多被采用;而非线性直接积分法适用范围更广,适用于除时间相关效应外的所有非线性行为,适用性强是其主要优点,在大震弹塑性时程分析当中多被采用。本文主要介绍非线性直接积分法的相关设置与应用。
1.时程分析的步骤
用户可以通过定义>函数>时程函数,进行时程函数的导入,通常我们可以采用来自于文件的方式将地震波文件导入ETABS中,目前支持的地震波格式主要为.txt或.dat文件。
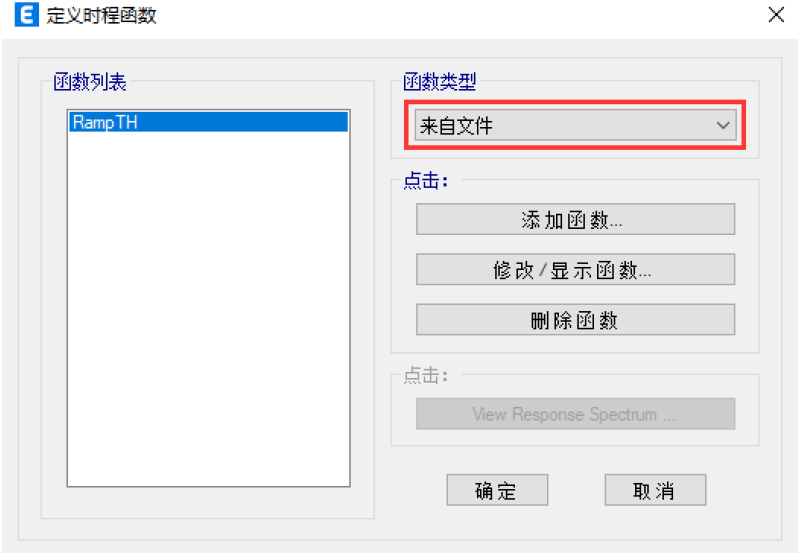
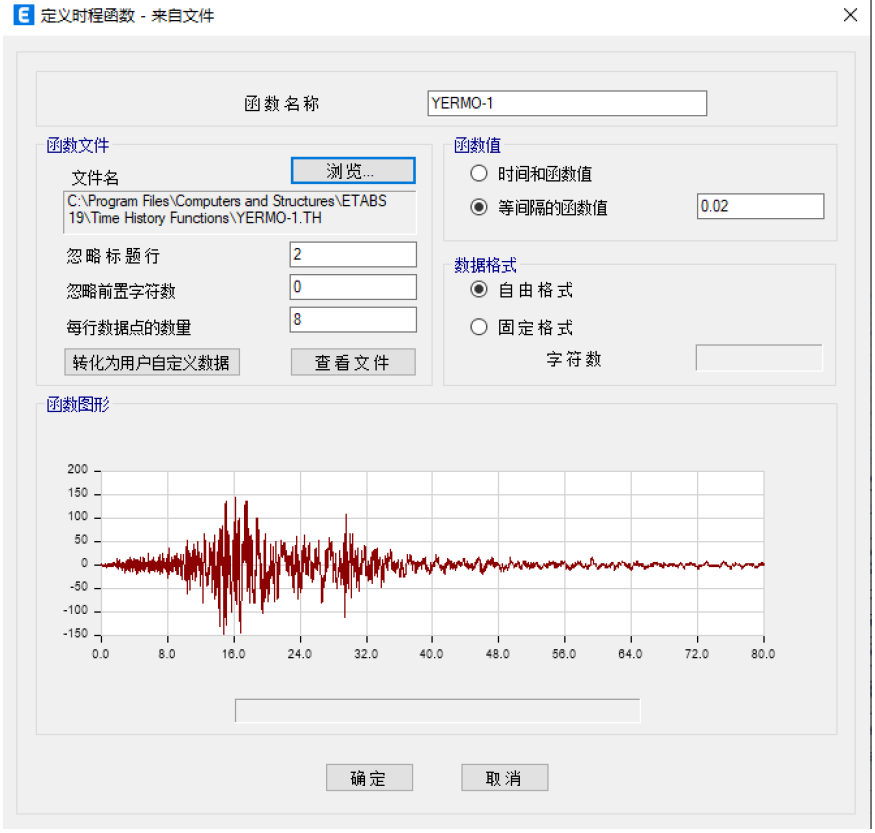
图1 地震波导入
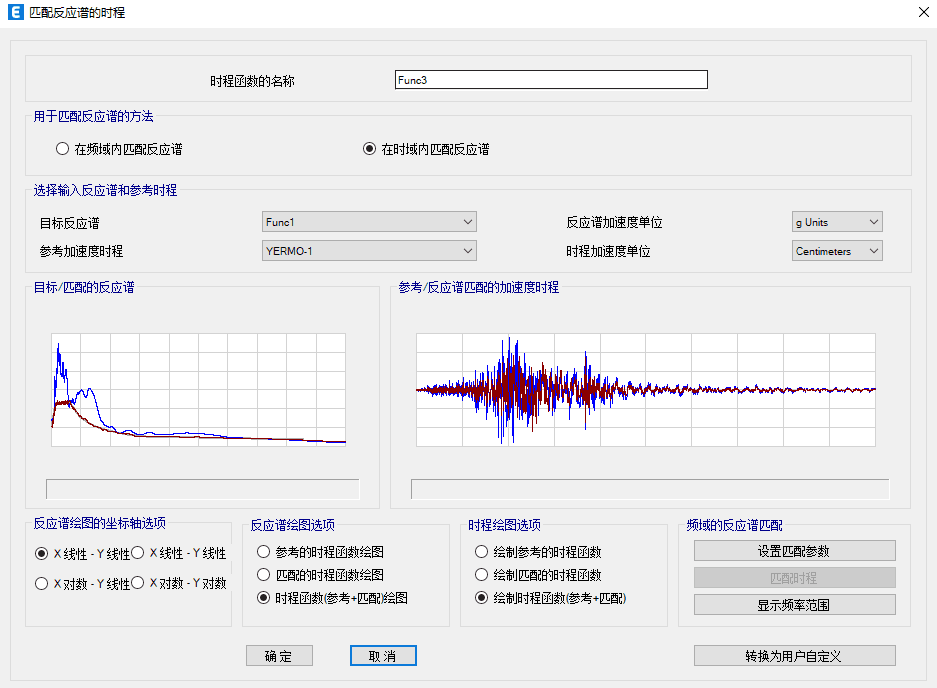
我国规范规定,时程分析中必须要采用一条人工波,ETABS可以通过匹配反应谱的方式生成人工波。ETABS在生成人工波时,不但考虑了人工波要在频谱和幅值上与反应谱吻合,还考虑了地震波的持时特性。从图2中可以看出人工波(红色曲线)与天然波(蓝色曲线)的持时特性吻合得很好。生成人工波的方法有两种,一种为频域方法,另一种为时域方法。一般来讲,时域方法匹配的效果更好一些,但是花费的时间更多。

1.2 初始重力工况
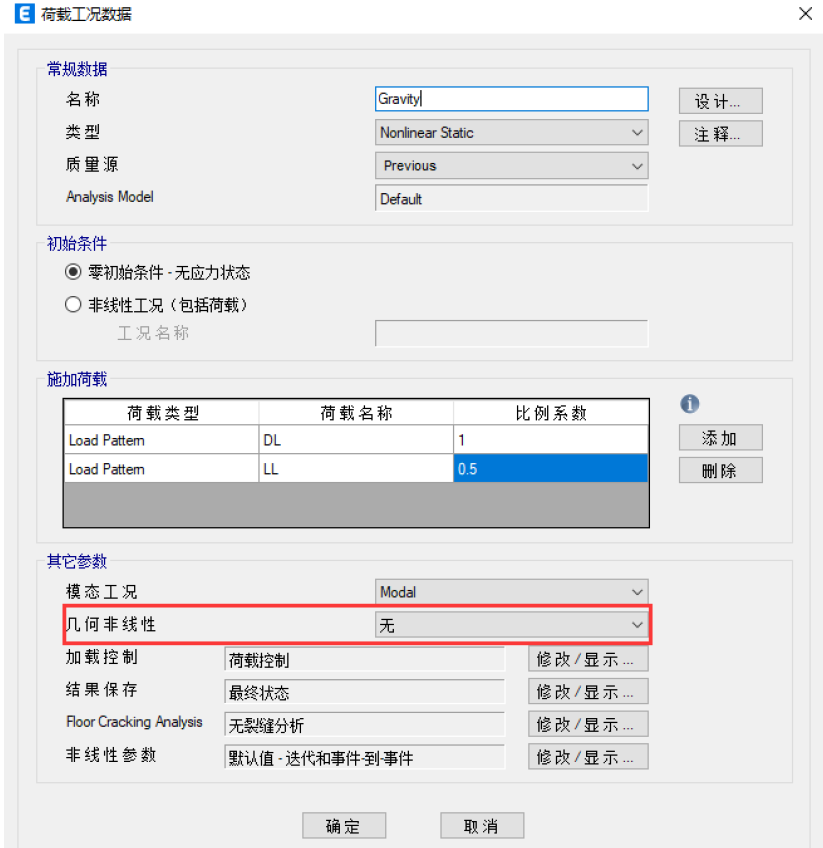
在进行非线性时程分析之前,需要先对结构施加重力荷载,重力荷载通常使用非线性静力工况或者阶段施工工况模拟,某些情况下也可采用非线性时程工况模拟。用户需要注意的是,前置的非线性静力工况或阶段施工工况 应采用与后续的非线性时程工况相同的几何非线性设置,这样可以确保前后工况几何刚度矩阵的一致性,否则可能会出现计算结果异常或无法收敛等情况。用户可以通过定义>荷载工况,工况类型选择“Nonlinear Static”或“Nonlinear Staged Construction”定义重力工况。
用户可以通过定义>荷载工况,工况类型选择“Time History”和“Nonlinear Direct Integration”,添加一个非线性直接积分法时程工况。
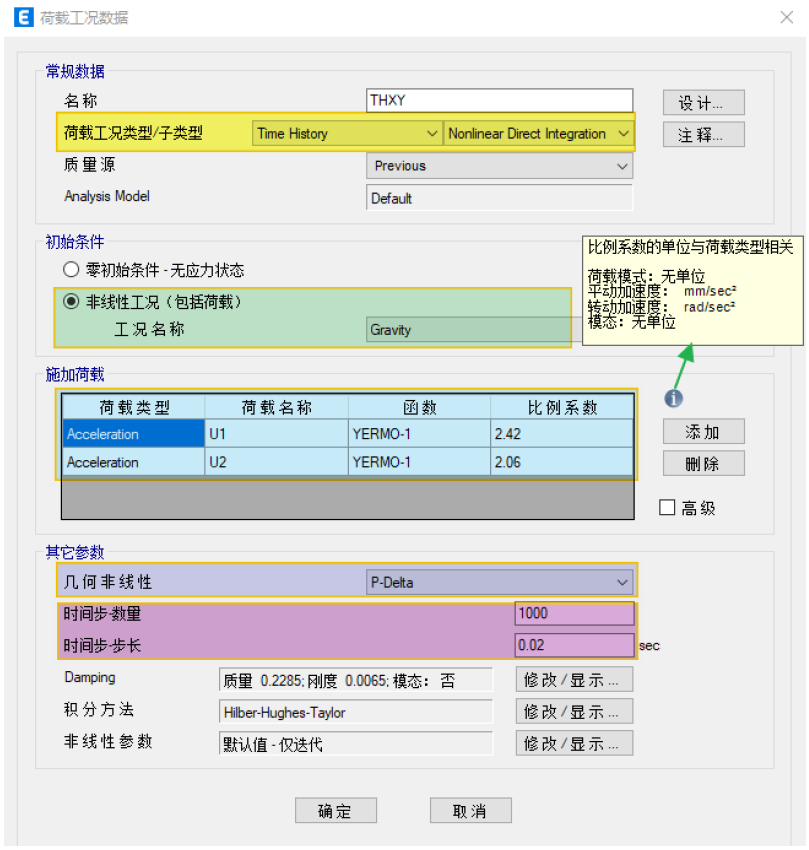
阻尼、时间积分方法和非线性参数设置由于涉及内容较多,在下文中详细展开讨论。
2. 阻尼设置
ETABS中有两种设置阻尼的方式,一种为瑞利阻尼,一种为模态阻尼。瑞利阻尼是在直接积分时程分析中常用的阻尼形式。
ETABS和SAP2000都允许用户在直接积分时程分析工况中采用模态阻尼。当用户采用模态阻尼的形式时,阻尼矩阵按下式确定:
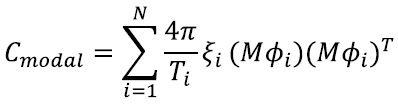
其中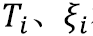 和
和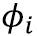 分别是模态i的周期、阻尼系数和振型;N是模态总数,由最大频率控制。图5左图红框部分为瑞尼阻尼设置框。图5左图蓝框部分为模态阻尼设置框,这里需要输入考虑模态阻尼的最大频率值。点击下方按钮弹出图5右图所示对话框,用于详细定义模态阻尼数值。
分别是模态i的周期、阻尼系数和振型;N是模态总数,由最大频率控制。图5左图红框部分为瑞尼阻尼设置框。图5左图蓝框部分为模态阻尼设置框,这里需要输入考虑模态阻尼的最大频率值。点击下方按钮弹出图5右图所示对话框,用于详细定义模态阻尼数值。
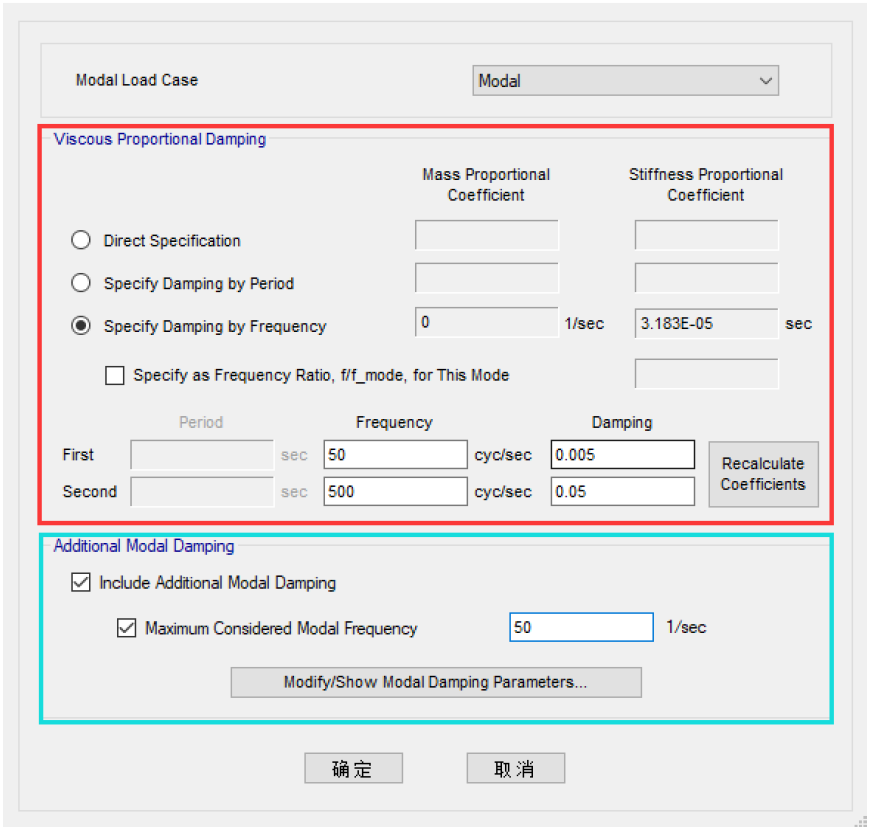
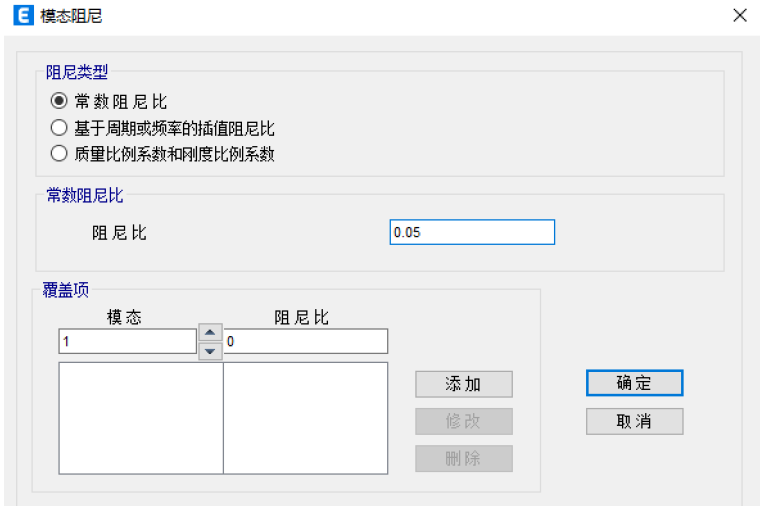
图5 阻尼设置
为验证上述讨论,现对某结构进行非线性直接积分时程分析,阻尼设置分别采用“仅模态阻尼”与“模态阻尼+刚度比例阻尼”的两种形式,为考察阻尼的作用,模型并未包含材料非线性,计算结果如图6中所示。可以看出,如果不考虑刚度比例阻尼的话,高频能量逐渐累积,计算结果整体呈发散状,而考虑刚度比例阻尼后,高频能量被耗散,高频振动被有效控制。

图6 不同阻尼设置下的结构响应
ETABS中包含了多种时间积分方法,如图7,均为隐式算法。
详见可参考学习帖子:
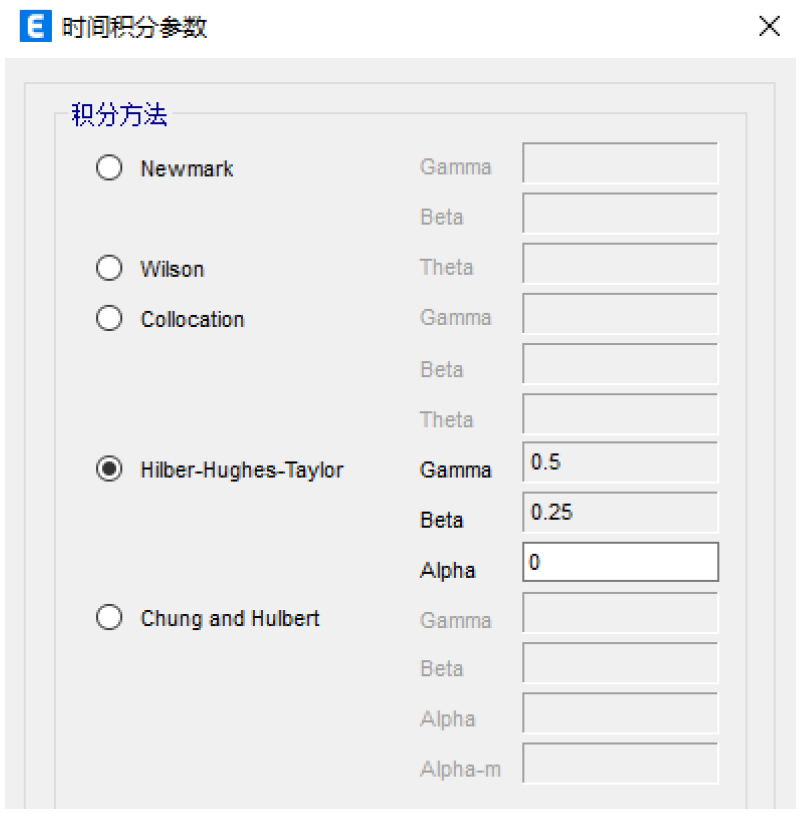
图7 时间积分参数
本文主要介绍Newmark方法和Hilber-Hughes-Taylor α方法。
Newmark方法
直接使用泰勒公式展开可得到下述方程:
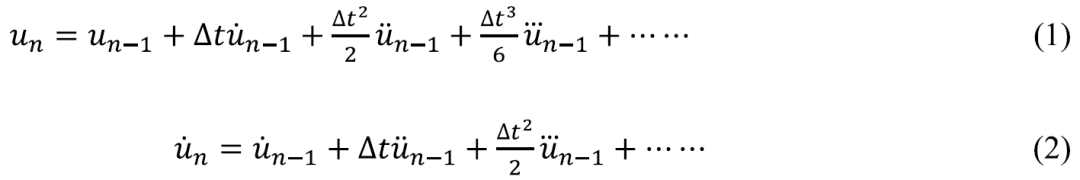
将这些方程截断并以下式进行表达:
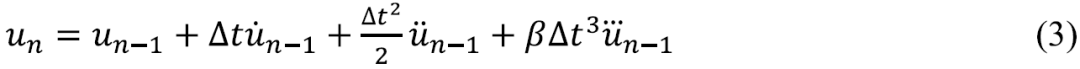
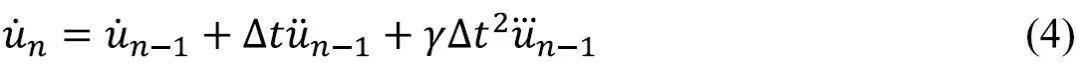
假定加速度在时间步长内是线性的,


当γ=1/2及β=1/4时,Newmark方法与平均加速度法相同,这种方法在Perform3D中被默认采用;当γ=1/2及β=1/6时,Newmark方法与线加速度法相同。当γ大于1/2时,会引入误差,这些误差与数值阻尼和周期延长有关。
Hilber-Hughes-Taylor α方法
α方法是使用Newmark方法求解下列运动方程:

α的取值范围为[-1/3,0),α为算法阻尼,α值越小,阻尼越大,当α等于0时,此方法退化为平均加速度法,无算法阻尼。α值会在高阶模态中产生数值能量耗能,产生类似刚度比例阻尼的效果,但是不相同的是,α值引起的数值阻尼会随着时间步长的减小而减小,对于常规的地震波间隔,α值取为-0.05~-0.02是合适的。这种方法在ETABS中为默认方法,我们也建议用户采用这种时间积分方法,并设置恰当的α值。
4.非线性参数介绍
非线性参数中主要讨论求解策略的选择,目前ETABS提供了三种求解策略:“仅迭代”(Iterative Only)、“迭代+事件到事件”(Iterative Event-to-Event)以及“仅事件到事件方法”(Event-to-Event Only)。
仅迭代(Iterative Only)。ETABS中提供了两种迭代方法,一种为常刚度迭代(如图9左),另一种为NR迭代(如图9右)。这两种迭代方法各有优劣,常刚度迭代法由于切线刚度矩阵只需要计算一次,因此每一次迭代的速度比较快,但所需的迭代步数比较多,适合一些非线性程度比较低,比较容易收敛的结构;NR迭代由于每迭代一次就要生成一次切线刚度矩阵,在此会花费较多时间,但是收敛所需的步数较少,当结构可能出现强非线性,或者需要考虑大位移等效应时,建议采用NR迭代。程序默认常刚度迭代次数为10次,NR迭代次数为40次,程序会优先采用常刚度迭代,如果达到迭代次数而无法收敛则改用NR迭代。
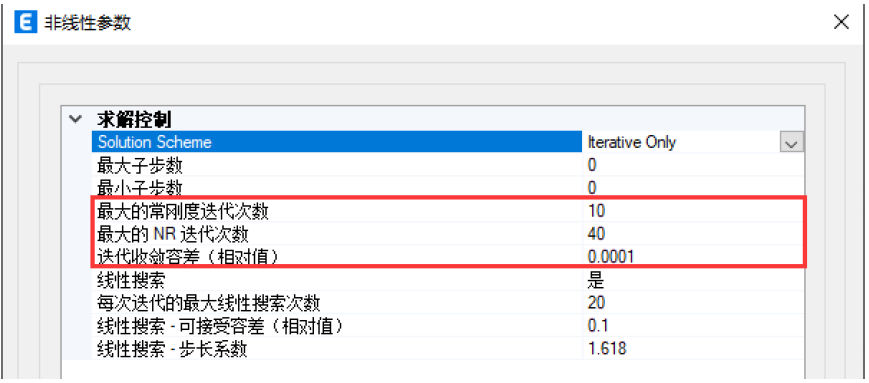
图8 仅迭代的求解策略
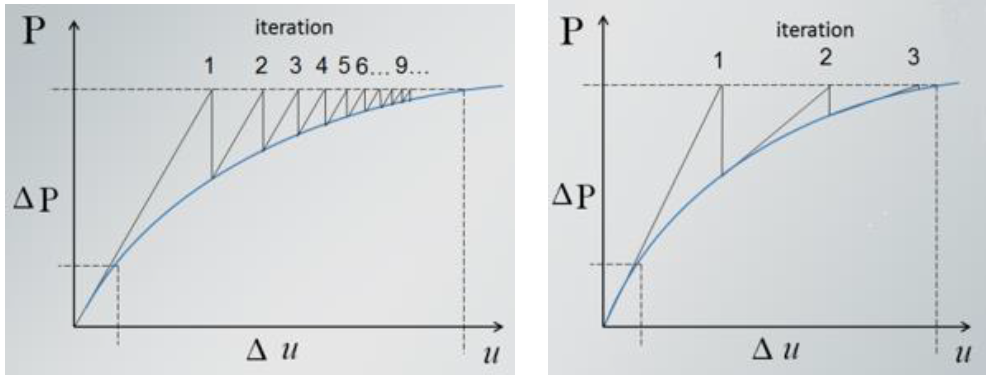
ETABS中采用力的迭代收敛容差,默认的相对容差值为0.0001,这一般来讲是比较小的,对于常规结构0.01~0.001的相对容差值是合适的。适当减小收敛容差对分析的收敛性,以及计算时间的减少都有很大好处,而对精度的损失并不大。但是对于索、膜等需要考虑大位移效应的结构,建议使用默认的相对收敛容差,甚至更小的收敛容差。对于大型模型,“仅迭代”的求解策略是我们比较推荐的,其优点是计算时间短,且有不错的收敛性。
仅事件到事件(Event-to-Event Only)。事件到事件方法是一个更加线性化的算法,这种方法仅在触发“事件”后才修正结构刚度。当构件发生屈服、从铰骨架曲线的B点向C点过渡、卸载等行为时,程序判定触发“事件”。事件到事件的方法每一步会产生微小的不平衡力,但是这些不平衡力并不会在整个时程范围内累积。如果采用“仅事件到事件”方法,不会出现收敛失败的情况,但是用户需要在分析日志文件(.log文件)中查看不平衡力是否可以接受。“仅事件到事件”的方法适用于框架铰、分层壳、具有多段线性塑性/缝/钩/摩擦摆/三摆行为的连接单元。注意,对于使用damper(粘滞阻尼器)单元、Wen塑性单元和橡胶隔振器等连接单元的结构,以及带有索等需考虑大位移的结构不应使用“仅事件到事件”方法。
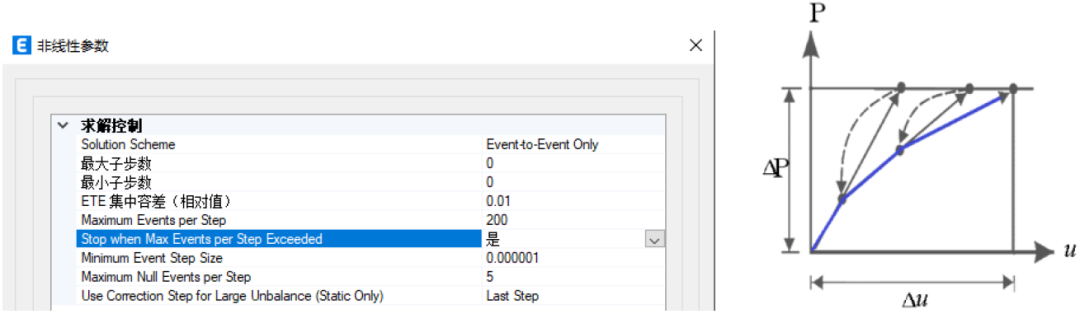
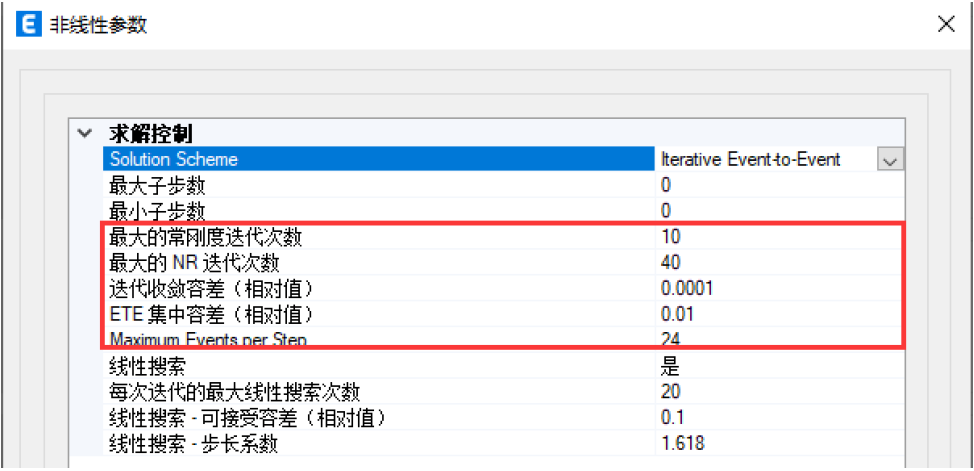
图11 迭代+事件到事件的求解策略
其他的选项设置限于篇幅不再展开,用户可使用默认值,或参考最新版《CSI分析参考手册》进行相关设置。
5.其他注意事项
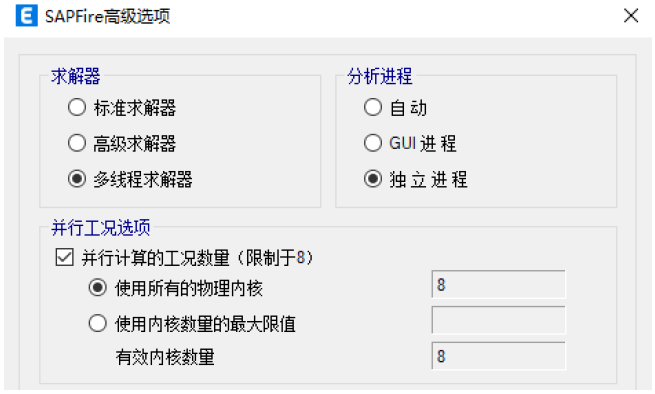
求解器。ETABS中有三个求解器,分别是标准求解器、高级求解器和多线程求解器,可以通过分析>SAPFire高级选项进行求解器设置。一般来讲,我们推荐首先采用标准求解器求解模态结果,由于标准求解器会给出所有警告信息,建议用户处理掉所有警告,然后再采用多线程求解器进行非线性时程分析。提前处理警告信息,不但能提高后期非线性分析的收敛性,也可以大大缩短分析时间,达到“磨刀不误砍柴工”的效果。
此外如果选择了分析进程中的独立进程,程序可以同时运行多个时程工况,时程工况的数量目前不超过8个或CPU物理内核的数量。

铰的模拟。ETABS目前有两种模拟铰的方法,一种是单元属性,另一种是连接单元。用户可以通过分析>非线性铰的分析模型选择铰的模拟方法,如图13所示。这里我们强烈推荐采用单元属性,采用单元属性的收敛性和计算时间均远远优于使用连接单元。采用连接单元的优势在于适用于FNA法,但是FNA法并不适合于大量非线性行为的场合,另外如果存在分层壳、单拉杆件、索或者需要考虑几何非线性的情况下,FNA法并不适用。因此,大多数情况适合采用单元属性模拟铰。
6.小结
本文首先介绍了非线性时程分析的基本步骤。注意,在定义初始重力工况和非线性直接积分法时程工况时,应保持前置工况与后续工况的几何非线性设置一致。
接下来,详细介绍了阻尼参数的设置。使用模态阻尼时,应添加刚度阻尼以耗散高频能量;时间积分法的选择与参数设置,特别是Hilber-Hughes-Taylor α方法中α的作用与取值,适当的算法阻尼可以过滤不必要的高频成分;非线性参数中求解策略的特点与适用情况,“仅迭代”方法,计算速度快,适合大部分情况,“仅事件到事件”方法不会收敛失效,但是需要用户校核不平衡力,而“迭代+事件到事件”方法虽然牺牲了一些计算速度,但是在时间步内会满足收敛容差,是程序的默认方法。
最后介绍了求解器的类型,推荐首先采用标准求解器求解模态结果,处理掉所有警告信息,然后再采用多线程求解器进行非线性时程分析。此外,关于铰的模拟方式,推荐采用单元模拟的方式。



.png?imageView2/0/w/480/h/270)

