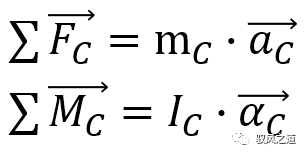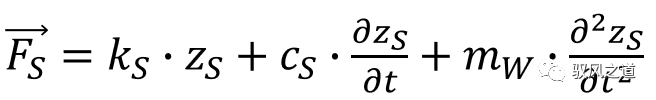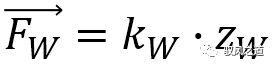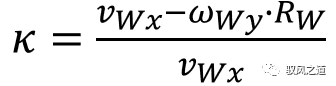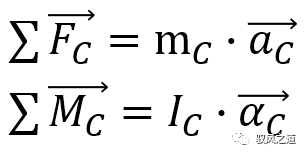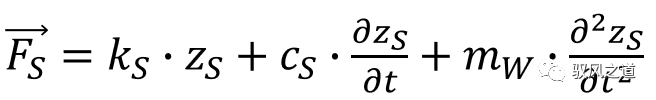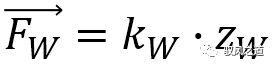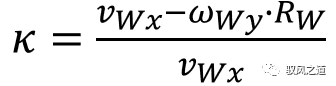车辆动力学的数学描述 - part 2:微分方程
在part 1,讲述了车辆动力学的运动描述,其采用16DOF模型。本文将基于16DOF模型,介绍相对应的微分方程。根据part 1,整车可分为车身、悬挂、车轮三个相对独立的部分进行分别研究。
1 基础说明:
相关下标声明:
2 车身系统
根据理论力学知识,刚体所受所有外力作用,可以等效为一个作用点在质心的作用力和一个绕质心旋转的力矩。对于车身(此处包括发动机、传动系统、底盘组件及车灯、后视镜、电子设备等附属结构,即簧上质量部分),在车辆坐标系中存在: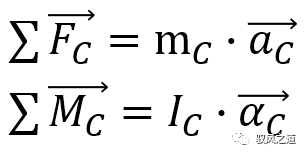
其中,车身受到的作用力包括自身及负载(乘员、货物、燃料等)的重力、空气作用力(阻力、升力、侧向力)、悬挂系统的作用力等3 悬挂系统
在16DOF模型中,悬挂系统被简化为仅在垂直于车身底面方向运动的单自由度弹簧-阻尼系统,其上方和车身下表面连接,下方连接车轮圆心。
对于单自由度弹簧-阻尼系统,可用一维振动微分方程进行描述:
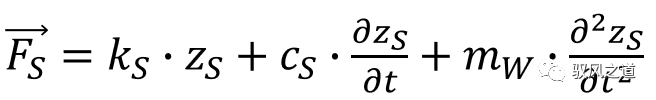
轮胎橡胶和地面接触部分存在缓冲作用,其影响是不可忽略的。对此,采用弹簧系统进行简化和表示,满足关系式: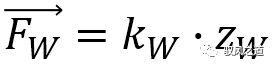
4 车轮系统
车辆运行过程中,车轮不会始终处于纯滚动状态。速度变化时,车轮存在纵向滑动,转向过程中还会存在侧向滑动。由于滑动的存在,轮胎的受力状态会发生变化。对于轮胎的滑移,通常定义两个参数:滑移角和纵向滑移率。滑移角定义为车轮坐标系X轴方向和悬挂系统的车身连接点的绝对速度之间的夹角,如图所示
纵向滑移率定义为滑移速度(车轮圆心纵向速度和旋转线速度之间的差值)与车轮圆心纵向速度的比例,其公式表达为:
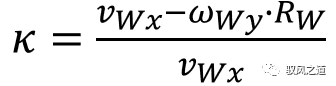
由于轮胎橡胶是强非线性材料,且内部充满气体,其受力状态的影响因素非常复杂,学术界提出了多种不同复杂度的数学模型,由于篇幅限制不进行详细描述。通常轮胎的受力主要影响因素包括轮胎滑移状态、轮胎垂向载荷、车轮倾角、路面状态等。对于赛车等激烈驾驶状态,还需要考虑轮胎气压、轮胎外表面温度乃至轮胎磨损程度等因素。
5 方程求解
从前述部分可知,车辆动力学方程是非常复杂的偏微分方程组,不存在解析解,只能依赖计算程序进行数值计算。
数值计算过程
目前商业上最常用的通用数学计算工具为Mathworks公司的MATLAB。与此同时,MSC Software的ADAMS、达索的Simpack等多体动力学(Multi-Body Dynamics,MBD)仿真软件也内置专业的汽车仿真模块,可方便快速地搭建不同复杂度的车辆动力学模型,并得到了汽车厂商的应用。
ADAMS软件汽车模块宣传图(图源:mscsoftware.com)