【CAE案例】流体振荡器流场模拟
01 研究背景
流体振荡器是没有活动部件的设备,根据流动入口的雷诺数及其几何形状的不同,能够在出口处产生均匀且可预测的频率脉动气流。流体振荡器的应用范围主要包括燃烧控制、改进翼型中的流动分离或减少阻力。

流体振荡器一直是许多实验和数值研究的主题,流体振荡器的CFD数值模拟大多基于雷诺平均方程(Reynolds-averaged Navier-Stokes equations,RANS)。
本案例使用了流体有限元仿真软件进行高分辨率数值模拟,为了能够更好地捕捉到振荡器内部的流场细节,采用了大涡模拟(Large eddy simulation,LES)的方法,以便更好地了解振荡器的流体动力学行为,模拟结果可用作基准测试参考。
02 模型建立
本案例中,振荡器的几何模型如下图所示。

由于康达效应(Coanda Effect),喷嘴产生的射流倾向于附着在壁的两侧之一。
例如,假设在特定时刻射流附着在底壁上,大部分射流将通过底部出口离开振荡器。
随后它的一部分将通过底部反馈回路再循环至入口处,导致射流改变方向附着在顶壁上并最终通过顶部端口离开设备,此过程循环往复,离开流体振荡器的射流即按照一定的频率改变方向。
计算中使用的流体雷诺数(基于入口宽度)为104。参考具有类似几何配置和等效雷诺数的实验工作中,流体振荡器的振荡频率为 15.4 Hz。模拟使用了以下网格:
网格 | 单元数 | 内部面 | 边界面 | 三维平面 |
A | 33355 | 49390 | 67995 | 1 |
A1 | 32425 | 48050 | 66025 | 1 |
B | 333550 | 794085 | 79560 | 10 |
B1 | 324250 | 772325 | 76600 | 10 |
对A、A1网格,计算采用URANS k-omega SST湍流模型,对B、B1网格,计算采用LES Smagorinsky模型,对于B1网格同时使用URANS k-omega SST进行计算,作为对比。
每次计算模拟 40 秒,采用0.001 秒的恒定时间步长,从而总共进行 40000 次时间迭代。
此外,对时间使用二阶差分格式(仅用于 LES 模拟)和 RHS 重建,压力为5,速度为10。对速度采用中心差分格式求解,求解器的参数保留为默认值。最后,将梯度重建改为使用最小二乘初始化(imrgra = 5)的迭代重建。
03 结果分析
模拟结果都很好地描述了振荡器基本的物理特性,并预测了与实验大致相似的振荡频率,不同网格的具体结果有一定差别。
为了比较,绘制了每个出口的流速关于时间的函数图像,并进行快速傅里叶变换分析(FFT),代表性的模拟结果如下图所示。
频率、最大和最小流速列于下表中。由于存在再循环,流速会出现低于零的情况。
湍流模型 | 网格 | 频率 | 最大流速 | 最小流速 |
URANS k-omega SST | A | 13.33 | 0.96 | 0.09 |
URANS k-omega SST | A1 | 14.82 | 1.70 | -0.68 |
URANS k-omega SST | B1 | 14.82 | 0.49 | -0.19 |
no model | B | 13.37 | - | - |
no model | B1 | 15.17 | 0.50 | -0.19 |
LES Smagorinsky | B | 17.19 | - | - |
LES Smagorinsky | B1 | 16.29 | 0.47 | -0.17 |
LES WALE | B1 | 17.78 | 0.48 | -0.17 |
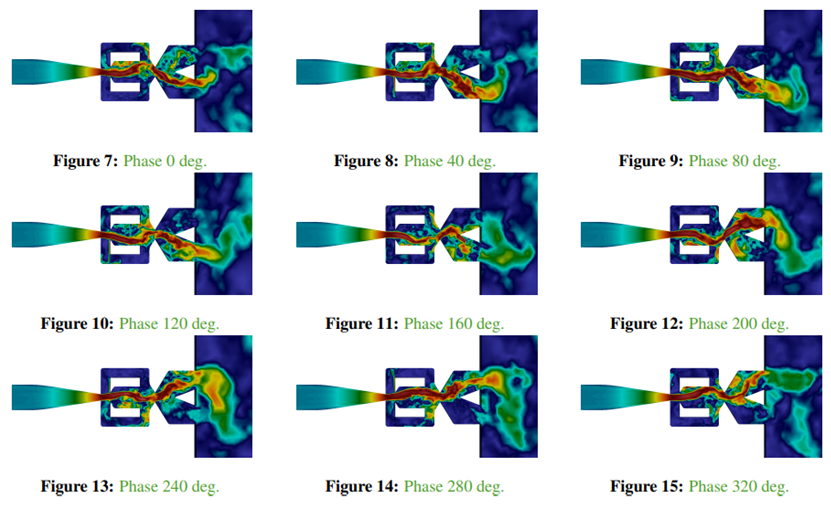
LE模型的模拟结果速度云图如下图所示,可以看出,LES 模型的模拟结果展示了更详细的流体流动状态。
04 结论与展望
通过采用多种网格和湍流模型进行了流体振荡器的数值模拟,验证了流体有限元仿真软件对流体振荡器模拟的适用性和准确性。
URANS k-omega SST 模型和 LES Smagorinsky 模型都能求解振荡器的物理特性,如振荡频率等,其中LES Smagorinsky模型能更好地捕捉到流动细节。
更多资讯可登录格物CAE官方网站
或关注服务号【远算云学院】
期待您的关注