【科研分享】韧性概念之新型阻尼器研发及相应结构需求指标评估
00
小编寄语
Angus' opnion
Hi, 大家好。时光荏苒,刹那间Angus 的假期已经接近尾声,有点不舍。2023年的开头注定又是不寻常的一年。土耳其的7.8级大地震,触目惊心的房屋倒塌,又给结构人上了一课。不管怎样,在过去的一年里,感谢大家的陪伴,也感谢很多分享软件教程的研究生同行们,相信在大家的共同的努力下,OpenSEES 的学习生态和商用价值会逐渐显现,为主流设计师接受,而不是局限于少数人,并一起为提高结构抗震做一些绵薄之力。
今天给大家分享一篇Angus 最新的paper。如果有兴趣,也欢迎和Angus 讨论,非常欢迎大家引用,谢谢支持。引用格式:
Ke K, Yam MCH, Zhang P*, Shi Y, Li Y, Liu S. Self-centring damper with multi-energy-dissipation mechanisms: Insights and structural seismic demand perspective. Journal of Constructional Steel Research 2023 Doi: https://doi.org/10.1016/j.jcsr.2023.107837

01
新型阻尼器研发
Development of newly dampers
随着韧性概念的渐热,各行各业都融合这个概念,韧性经济,韧性城市等等。在结构工程领域,朴素的韧性结构一开始仅用于描述结构的可恢复性,更为直接的,structural resilience 近似等于structural self-centring capacity. 在Angus 认知里,我更倾向于结构的韧性是更高的维度,不仅应该囊括结构的可恢复性,而应该间接等价于结构高性能属性。在基于PT后张拉或者SMA 的材料并联金属屈服机制耗能装置的自复位结构中,研究者经常会遇到一个结构性能的矛盾,自复位和耗能行为。进而,这类自复位结构为了优先确保自复位特征,其耗能行为大多数用modest 来描述。随着研究的深入,很多学者也提出了这类结构的高阶模态影响显著,对主结构不利,楼层加速度较大,对非结构构件安全不利。因此,研究者逐渐意识到,追求复位的同时应该综合的提高的结构的性能。
过去结构抗震相关研究已经说明,结构的地震响应是地震随机性的,即依赖于输入结构的地震的记录,实际上这个结构响应随机性的特征其实也隐含了结构本身对地震种类的敏感,而结构响应对地震种类的敏感则依赖于结构本身的力学属性(常常研究中通过结构响应的离散性来描述)。在可恢复性结构被热捧之前,大多数的结构都可以近似地等效为理想弹塑性系统(即结构滞回规则未丰富化,骨架曲线近似就是线性随动模型)。因此上述地震随机性的异同往往就被认为是地震的随机性。现在学者已经意识到,呈现出不同滞回参数的等待结构体系(结构近似等效,如一阶模态是近似的),在同一个地震激励下,结构的地震响应也是差别很大的。例如,在同一组地震输入下,对于仅屈服后刚度系数不同的结构体系,较大的屈服后刚度系数的结构可以有效的控制结构的高阶振型的不利影响,进而降低结构响应的离散性。听上去这类具有较大或者显著屈服后刚度系数的结构体系较传统理想弹塑性体系具备优势。但在另外一方面,这种具有显著屈服后刚度系数的结构的耗能能力则相对较小屈服后刚度系数的结构显著下降,因此结构的加速度响应则陡然提高,这不利于结构的非结构构件的安全。因此,在研究中,评估结构的性能应该尽量统筹兼顾,当然在必要的时候也要取舍有序。随着这种认知的深入,已经出现一批专门研究不同滞回规则的SDOF和MDOF在不同地震种类下的结构需求指标,进而在结构层次对所提出的结构的抗震性能进行定量的评估。
下面就来讲述这样的案例和写作论文的思想(以问题的形式展开)。
如何构造新型阻尼器?(发现性能进一步提升的空间)
回答这个问题,首先应该整明白为什么要构造阻尼器?我们提出新的阻尼器最快的方法自然是基于以往学者研究基础之上,根据自己所要解决的工程需求(research gap)进行改进,并达到解决研究问题最初设定目标。比如时下,在被动减震方向,阻尼器的研发成了一个热点。通过往结构上安装一个新型的阻尼器(如何按,也是个学问),把以往的设计和评估流程走一遍,文章就很快出来了。这样行文的文章是很多的。所以,你会看到越来越多看似很新颖的阻尼器构造,但是从机理上对现有的工程问题的解决效益不大,到工程应用则更是山长水阔。所以问题的焦点是为什么我们要构造新型阻尼器。对于这个问题的回答,就是我们构造阻尼器特征的方向。比如,Angus 阅读大量的高性能阻尼器支撑结构方面的文献,截至到目前为止,阻尼器支撑结构依然存在的问题如下(注意这里Angus 的研究的阻尼器支撑结构是自复位的,BRB支撑不在我的讨论范围内):尽管近些年学者意识到,同时提高结构的屈服后刚度系数和耗能能力,可以显著提高自复位阻尼器支撑结构的抗震性能(见图1[1])(因为兼顾主要受力构件和非结构构件,降低地震的软弱层风险),但是较大的屈服后刚度会使得阻尼器支撑的承载力较大,导致与阻尼器支撑相邻的构件和节点的需求增加,有增加其局部破坏的风险。此外,这类阻尼器[1]也被很多同行进行优化,但是构造依然是大同小异。Angus 认为在构造上此类阻尼器存在受压稳定性问题,摩擦片两侧是否可以有效持续均匀滑动变形,以及摩擦片的角度和摩擦系数无法解耦,设计可能缺乏灵活性。因此这样的阻尼器支撑的性能存在进一步优化的空间。

图 1 自复位摩擦阻尼器
阻尼器优化思想
意识到上述的问题,那么如何解决这些问题,就是阻尼器优化的指导思想。因此两方面开展优化流程。一是阻尼器的力学性能,二是阻尼器的构造。意识到尽管屈服后刚度可以有效控制结构高阶振型的不利影响,降低结构在地震下响应的离散性,提高结构的可靠性,但是持续的较大屈服后刚度的可能不利于局部构件连接(阻尼器支持结构为例,与支撑相邻的构件和节点域的强度需求较大,在强震下有潜在局部破坏的可能)。是否可以构造一个阻尼器支撑,在骨架曲线上呈现出多线性,如三线性。进而,其对应的支撑结构也是三线性。第一次屈服后刚度较大,用于控制体系的高阶振型影响,然后在预设层间位移角处,进行变刚度,即较小的第二次屈服后刚度,以实现强度和刚度解耦,降低阻尼器支撑对相邻构件或者节点域的强度需求,改善整体结构的受力合理性。其次,针对现在研究较多的楔形摩擦阻尼器存在的受压侧向稳定性,变形协调性和设计的灵活性(保证自复位前提下,摩擦系数和摩擦倾角非解耦,摩擦面倾角需要大于一定值,该值是较大屈服后刚度的一个原因)。是否可以在构造进行改进,通过增设一定复位元件和改变摩擦板布置,以解决上述问题?
Angus 也注意到,有些人学者如Fang[2] 和Qiu [3]在基于文献[1]的基础上,做了一些改进,主要地将竖向的高强螺栓碟簧组合替换成了SMA 螺栓,利用SMA 相变的特征,已经初步实现了变刚度的思想,但是依然没有解决在完全自复位前提下,摩擦系数和摩擦面倾角的耦联,设计过程中灵活性依然存在进一步提升的空间。此外,阻尼器的构造基本和文献[1]一致,受压侧向稳定性以及摩擦板变形协调性依然存在。
针对此,Angus 首先进行了概念设计,设计了如图2构造的阻尼器,基本解决上述的问题。首先在受力机理和构造层面上进行了优化。当然所提出的阻尼器,依然存在很多问题,比如使用的SMA 材料较多,构造较复杂,这些方面,也是作者持续的研究重心。
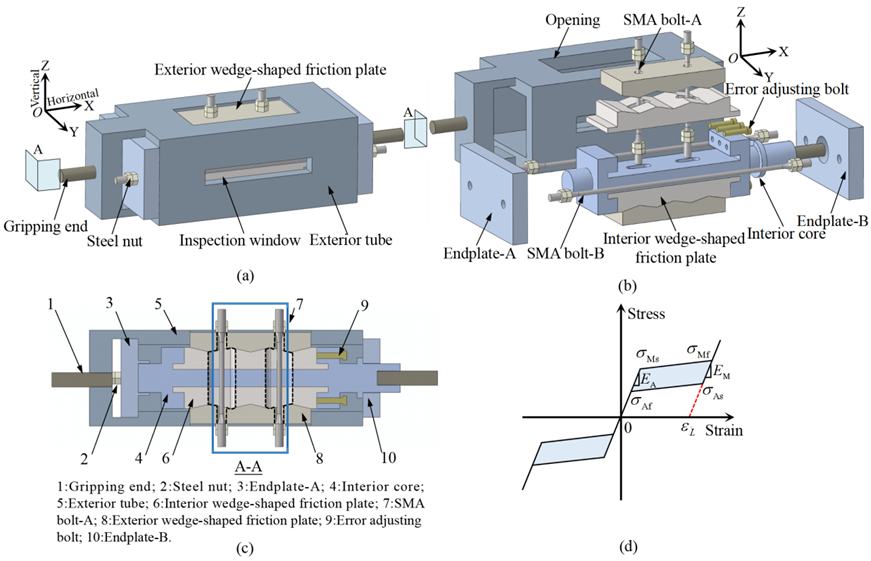
图 2 自复位摩擦阻尼器
所提出的阻尼器的工作原理和滞回曲线如图3和图4所示。
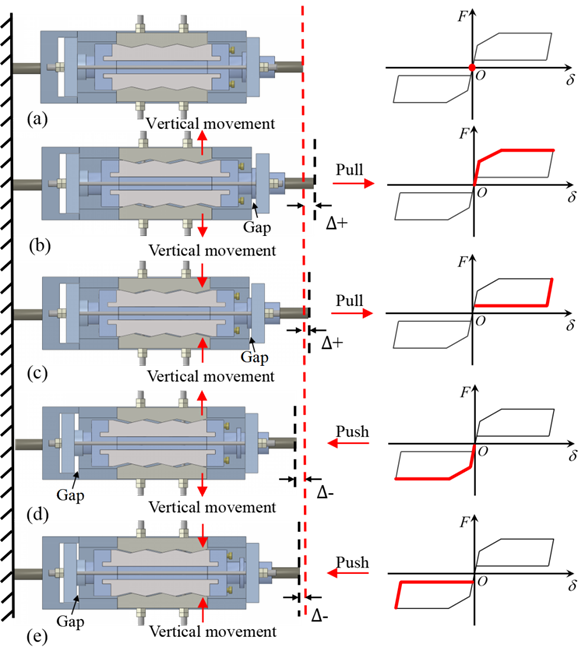
图 3 自复位摩擦阻尼器工作原理

图 4 自复位摩擦阻尼器滞回规则
根据图2-4,可见在构造这个阻尼器的想法是很简单的。如果想要增加侧向受压稳定性,则增加一个外套筒进行限位;为了提高摩擦机制的协调性,将两侧摩擦变为一侧摩擦;为解耦摩擦面倾角和摩擦面系数,增设水平复位元件(目前使用的是SMA,考虑是在提供复位的同时,进一步优化其耗能行为,当然,后期针对其造价高会作进一步优化)。通过概念设计,可以得到所提出的用于描述阻尼器的第二刚度退化的时刻的关键参数(这个参数的取值对结构控制高阶振型的效果是起到关键作用的,参数取值为0,则退化至最初的旗帜性规则,取无限大,则演变为文献[1]的滞回规则)是可调的,因此使得设计可以灵活。
阻尼器性能研究
在概念设计基础之上,为充分理解阻尼器的滞回性能,首先对阻尼器进行了理论分析和数值模拟。首先,根据受力分析,推到了阻尼器的理论滞回模型。阻尼器的滞回模型可以通过以下参考线进行描述。
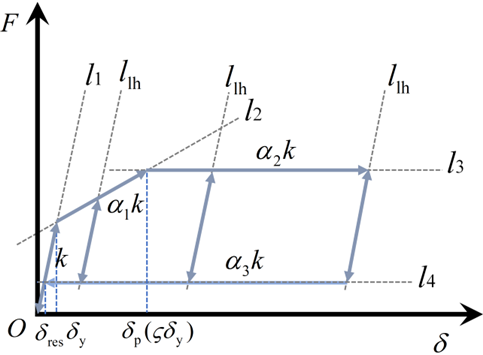
图 5 自复位摩擦阻尼器理论滞回规则
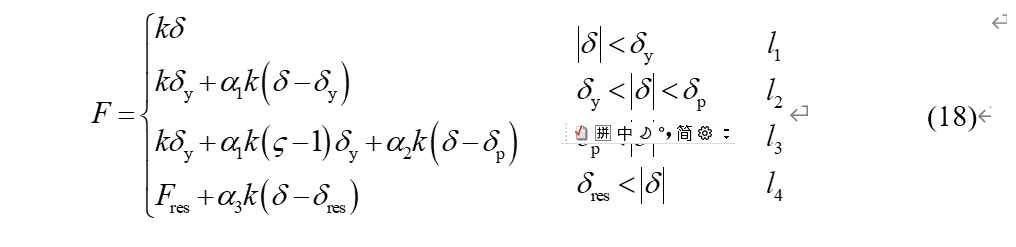
在此基础上建立了数值模型,如下图6,并进行了典型几何参数的参数分析。在此之前,进行了大尺寸SMA 的tension-release 滞回试验,如图7,得到了SMA 材料的材料特征参数。
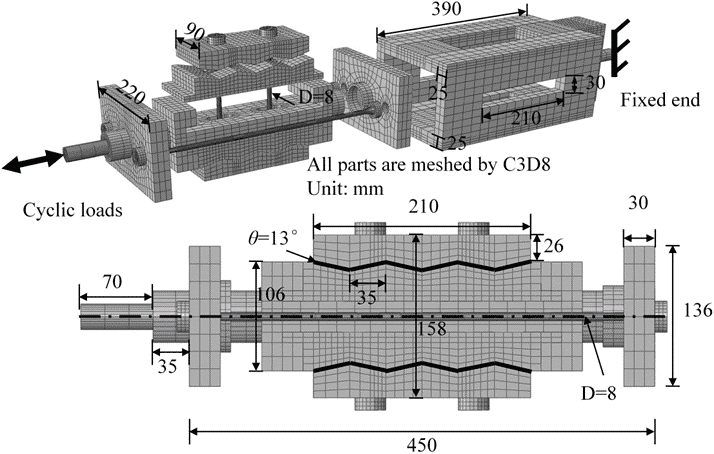
图 6 自复位摩擦阻尼器数值模型
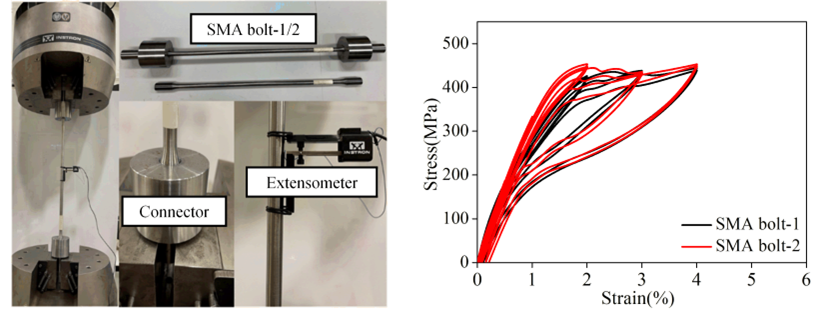
图 7 SMA 螺栓的滞回特征
根据有限元的结果,可以得到典型的滞回曲线对比结果,如下图8,并与理论模型对比如图9。
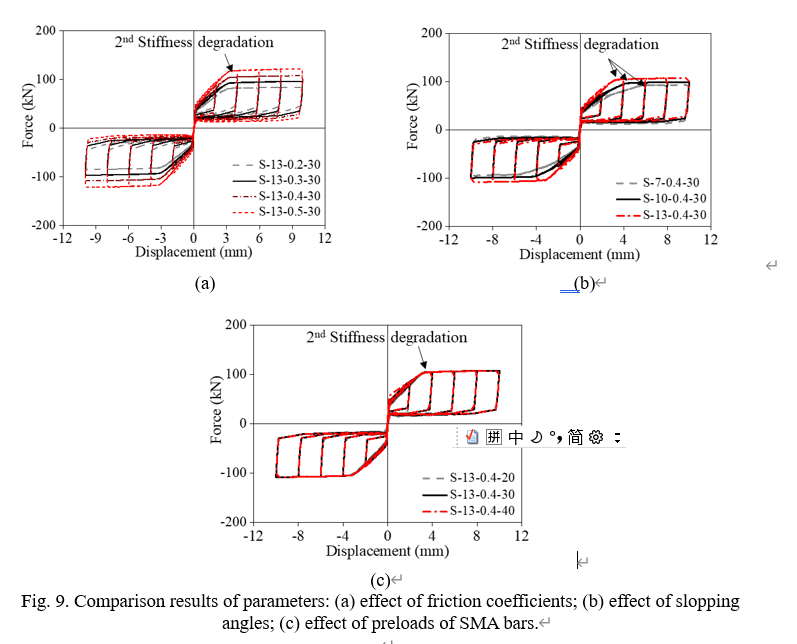
图 8 自复位摩擦阻尼器参数分析结果
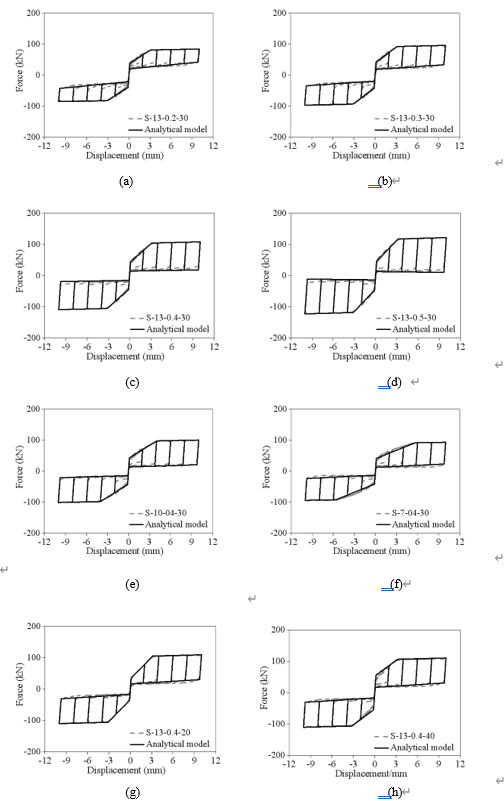
图 9 自复位摩擦阻尼器数值和理论的对比
上述的理论和数值分析,从两方面证实了该阻尼器的概念设计。当然阻尼器的试验验证也是不可或缺,目前第一批试验已经开始,试验试件各部分如下图10,试验结果将会在下一篇paper 中呈现。结合试验,理论,数值三种方法,所提出的阻尼的滞回性能将会被全面深入的理解。根据已有的结果,所提出的阻尼器实现了最初的设想,可以作为新一代高性能阻尼器。

图10 阻尼器试件
02
阻尼器支撑结构的需求分析
demands of braced structures with the proposed dampers
评估一个新型的阻尼器的优劣,从结构层次入手会更加简单和直接。为了说明该阻尼器的工程应用可行性。首先构建了阻尼器的一个应用场景,即阻尼器支撑结构,如图11。

图11 阻尼器支撑结构
阻尼器支撑结构的侧向力完全由阻尼器支撑承担,竖向荷载由重力框架承担。因此我们有理由相信阻尼器支撑结构的滞回规则和阻尼器本身滞回规则形状是一致的,也可以通过前面01节的理论滞回模型来预测,为方便表达,重新表达结构体系的静力滞回模型如下。
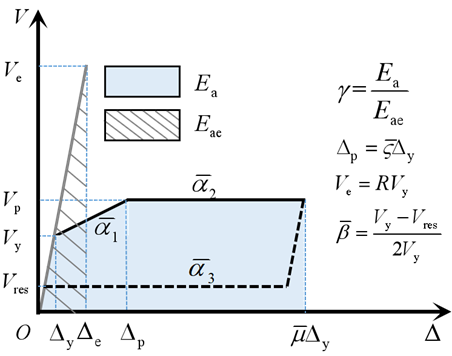
图11 阻尼器支撑结构滞回模型
接下来对阻尼器支撑结构进行需求层面的等延性谱分析,选取结构需求的两个指标:能量修正系数和加速度系数。能量修正系数指标可以用于评价结构的耗能性能;加速度系数可以检测体系的加速度响应。
结构的需求较强依赖于结构的周期,滞回参数的取值以及组合。因此为了合理的评估结构的需求指标,需要对阻尼器支撑结构各滞回参数进行合理地评估。考虑到阻尼器支撑结构侧向力学行为主要由阻尼器支撑提供。因此,了解阻尼器支撑的滞回参数是不可缺少的。以本文的阻尼器为例,构造的阻尼器支撑只是在阻尼器一端串联了一个弹性钢段。因此相比较阻尼器而言,阻尼器支撑仅仅改变了阻尼器的初始刚度。为此,利用01节提出的阻尼器的理论的滞回模型,考虑的参数有SMA 的直径和预紧力,摩擦力系数,摩擦力倾角,阻尼器的初始刚度,一共构建了900个阻尼器的模型,得到了各个滞回参数的散点图,如图12。根据此图可以大致得出阻尼器支撑的各滞回参数的合理变化范围。进一步,阻尼器支撑结构滞回参数的合理范围可以近似预估出来。
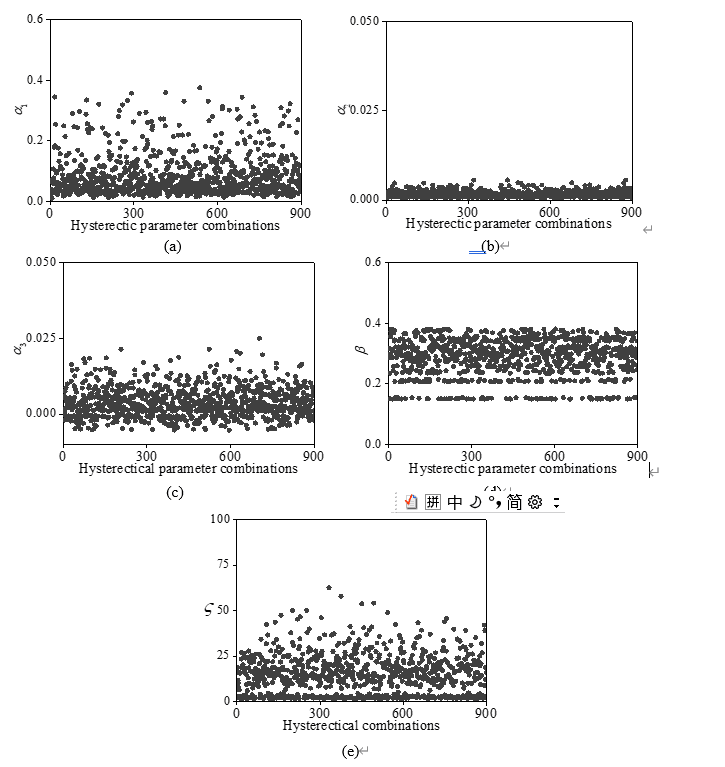
图12 阻尼器支撑滞回参数散点图
等延性ESDOF反应谱分析
首先需要明确的是,本文分析结构的对象是低多层阻尼器支撑结构。假定结构的动力行为可以完全由其一阶模态控制。而其一阶模态的的动力行为可以由其等效的单自由度ESDOF 描述(具有相同质量,周期,滞回参数)。进而结构的能量修正系数和加速度系数均可以通过ESDOF 系统进行求解。考虑到等延性反应谱计算需要占据大量的计算成本,即使利用OpenSEES这种计算效率较高的有限元软件建立的SDOF系统也需要花费一定时间,且OpenSEES 现有的材料库中没有本文提出的阻尼器的滞回模型单轴材料。因此,首先在OpenSEES 中开发了可以描述阻尼器滞回规则的单轴材料,MGSC material. 其次,为了提高ESDOF反应谱的计算效率,利用了Matlab &C++混合编程,建立了一站式计算反应谱各类指标的计算程序,BTESPEC。为验证计算程序的合理性,比较了OpenSEES 和BTESPEC 某一个ESDOF计算案例的动力结果如图13.
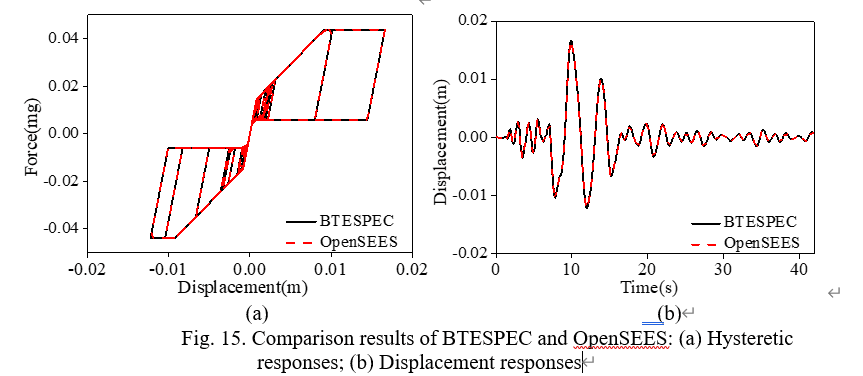
图13 OpenSEES 和BTESPEC计算对比图
基于上述的陈述的基础,开展了大量的代表低多层阻尼器支撑结构的ESDOF系统的谱分析。同时为了和先前提出阻尼器支撑结构(典型旗帜型和带有摩擦的旗帜型,见图14)进行了对比,也展开了其余两类结构的相应谱分析。
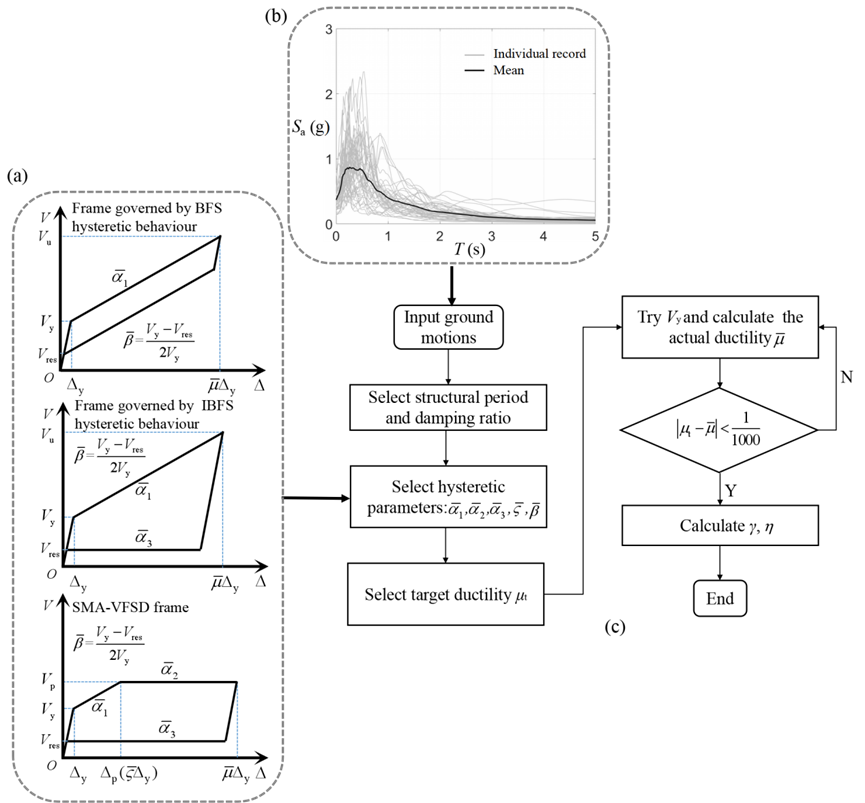
图14 谱分析流程
ESDOF 谱分析结果分析
图15和16呈现的是典型参数下三类结构能量修正系数和加速度系数的对比结果。由图15可知,本文所提出的阻尼器支撑结构的能量系数在目标周期 区间类都是最小的,说明提出的阻尼器支撑结构在三类结构中耗能能力是最好的,可以显著降低地震输入结构的能量。此外,图16可以清楚的表达出,所提出的阻尼器支撑结构相较于其余两类结构可以显著降低结构的加速度响应,进而可以进一步保护非结构构件。

图15 能量修正系数对比结果
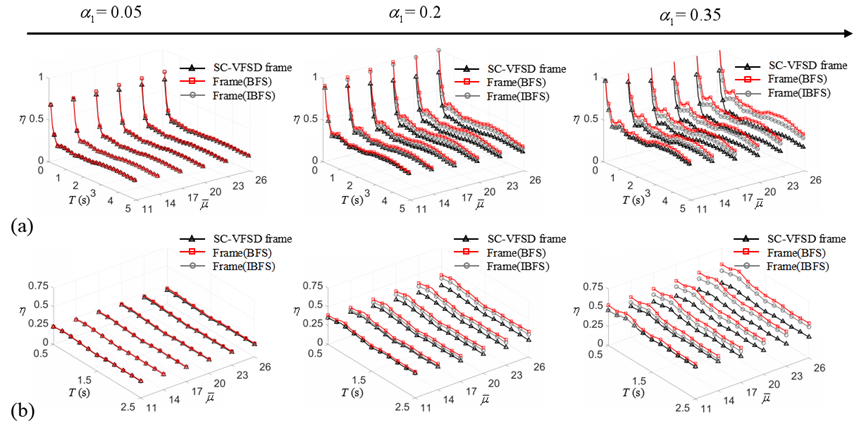
图16 加速度系数对比结果
03
存在的问题和总结
Issues and conclusions
本文从静力的构件层次和动力结构层次对笔者提出的阻尼器以及其潜在的工程应用进行了初步的探索。写本文的初衷是想给后来人一点写作的思路,如何发现研究的gap,如何解决问题,如何评估你解决问题的方法,最后总结。
亟待解决的问题
本文提出的阻尼器支撑结构的抑制高阶振型的有效性需要直接从MDOF系统证明;
本文提出的阻尼器的构造虽然解决了稳定性,但是构造复杂,且成本高;
本文提出的阻尼器支撑的变形能力需要进一步优化。
本文总结
所提出的阻尼器呈现出多阶段耗能特征,且设计参数解耦可以灵活根据其在结构中的需求灵活设计;
理论和数值模拟预测的阻尼器滞回行为结果一致,试验验证正在进行;
ESDOF 谱分析结果表明,相较于以往的两类自复位支撑结构类型,所提出的阻尼器支撑结构耗能能力是最优的,加速度响应是最低的,证实了本文提出的阻尼器的潜在工程价值。





