1D/2D/3D单元仿真精度的对比和研讨
有限元仿真的实质就是将分析对象离散成一个个独立的、相互之间通过节点连接起来的单元的集成,商用CAE软件都能提供各具功能的0D/1D/2D/3D不同维度单元类型,那如何选用才能兼顾计算精度和求解效率呢?很多情况下一个模型既可以采用3D单元,也可以采用2D或者1D单元进行建模、网格划分和求解,那么同样的分析模型而选用不同单元类型,它们的求解精度有何不同呢?
本文以悬臂梁承载后计算其最大扰度为目标,先采用材料力学中经典理论公式进行计算并以此结果作为后续仿真计算的基准值,采用Simcenter Nastran求解器并选用SOL101线性静力学解算方案类型,采用不同的单元类型并分别求解和对结果进行对比,这样直观地判断不同单元类型计算后的精度,进一步研讨1D梁单元特点及其工程应用场合。
1. 理论计算
1.1 模型参数
如图1所示矩形薄壁方管的悬臂梁结构作为本次分析的基础模型,长度为L=0.5m,截面尺寸为40mm×40mm,壁厚为2mm,左端面固定(6个自由度全部固定),右端面承受向下的集中载荷F=100N,计算该悬臂梁最大弯曲扰度ymax(-Y向最大变形位移)。
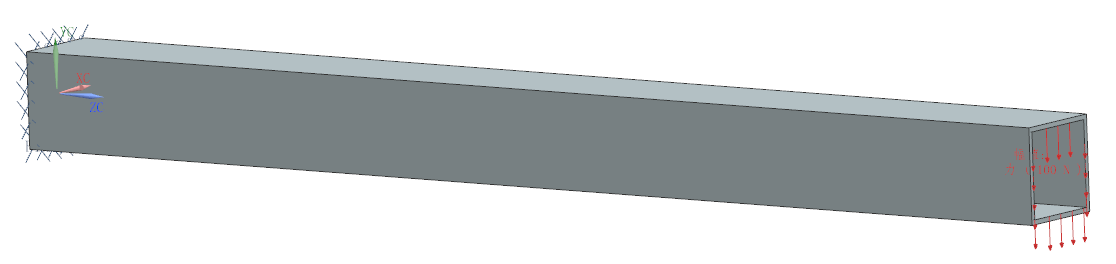
图1 悬臂梁结构及其边界条件示意图
材料设为NX材料库中的Steel,其参与计算的性能参数及其数值主要为:弹性模量为E=206.94Gpa,泊松比为μ=0.288。
提醒两点,一是不管采用理论公式进行计算,还是软件操作过程中数据的手动输入,都需要注意单位的合理换算,二是本案例不计入分析模型自身重量对计算结果的影响,也就是说,大型梁结构件力学性能计算必须考虑自重的影响,并且还要考虑施加环境条件(比如温度的变化)和工况载荷(比如风载)。
1.2 计算方法和结果
根据材料力学中悬臂梁扰度计算的理论公式ymax=F*L3/3*E*I,其中I为矩形薄壁管的截面惯性矩,在建模环境中利用分析分析\截面惯性命令,如图2所示选中截面上的8条棱边线并确认后即可测量截面惯性矩大小为7.3365e+04mm4,进一步把各个参数代入公式后便可得到其最大扰度理论值为ymax=0.2744mm(具体计算过程不再赘述)。
提醒:由于上述模型的截面中忽略了过渡圆弧,因此不能选用《机械设计手册》中提供的矩形截面惯性矩值,即需要采用软件测量命令来实测相应的数值。
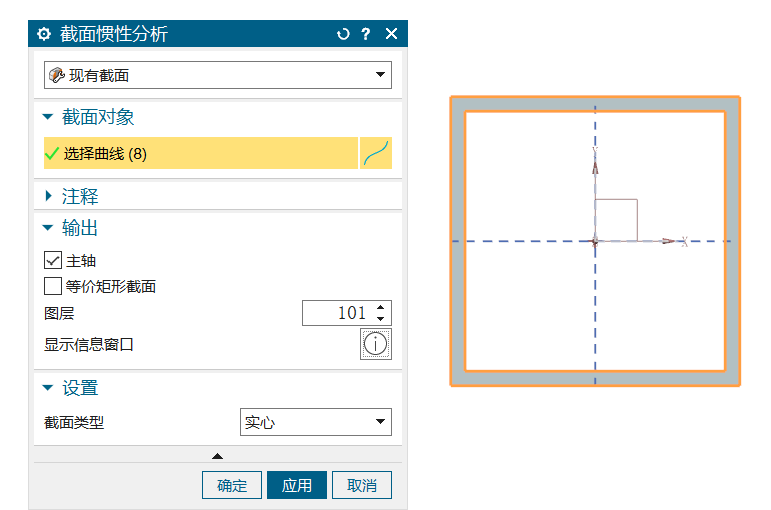
图2 截面惯性分析对话框
2. 采用Simcenter Nastran计算
2.1 采用3D单元计算
3D单元有四面体、五面体和六面体三大类型,而每个类型单元又有1阶和2阶之分(同样大小的2阶单元相比于1阶单元,节点数量更多,所以其计算精度更高,但计算时间和成本大大增加),考虑一般性本次计算采用六面体8节点1阶单元CHEXA(8),单元大小为1mm,通过仿真计算得到的Y向(负方向)最大位移云图,如图3所示,最大变形位移为0.283mm。

图3 3D单元计算的位移云图
建议在上述基础模型基础上,修改3D单元类型(包括不同阶次)、单元大小后再进行求解,查看结果的变化情况。
2.2 采用2D单元计算
2D单元包括CTRIA3(三角形3节点)、CTRIA6(三角形6节点、2阶单元)、CQUAD4(四边形4节点)和CQUAD8(四边形8节点、2阶单元)等类型,本次计算采用CQUAD4 单元,单元大小为5mm,通过仿真计算得到的Y向(负方向)最大位移云图如图4所示,最大变形位移为0.284mm。
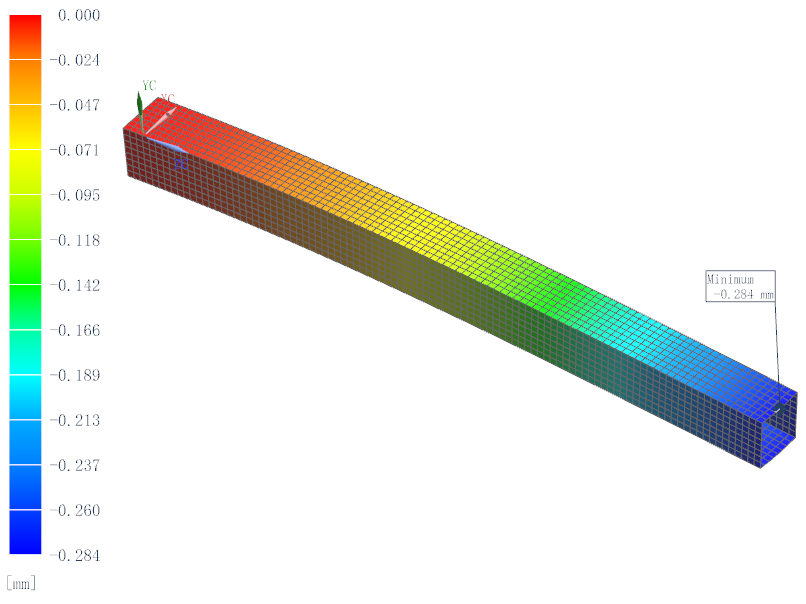
图4 2D单元计算的位移云图
建议在上述基础模型基础上,修改2D单元类型、单元大小后再进行求解,查看结果的变化情况。
2D单元类型主要应用在薄壁和壳体类零件,上述悬臂梁具有等截面的特点并且长度比截面尺寸大得多,就可以采用以下的1D梁单元来仿真,这样减少了单元和节点的数量。
2.3 采用1D单元计算
1D梁单元包括CROD、CBAR、CBEAM和CTUBE等单元类型,本次计算采用CBAR单元,节点数量为5,通过仿真计算得到的Y向(负方向)最大位移云图如图5所示,最大变形位移为0.279mm。
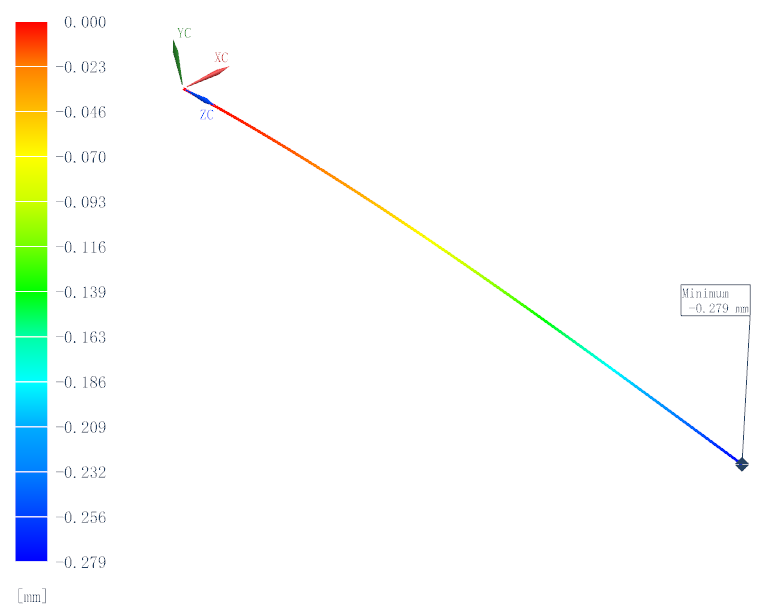
图5 1D单元计算的位移云图
建议在上述基础模型基础上,修改1D单元类型、单元或者节点的数量后再进行求解,查看结果的变化情况。还可以查看1D梁长度方向任何位置截面上的变形和应力结果。
学习上述具体操作流程和求解方法,可以登录仿真网并关注笔者发布的相关教学视频课程:《NX CAE/Simcenter 3D入门基础课40讲》(免费)、《NX CAE/Simcenter 3D静力学分析基础入门41讲》、《NX CAE/Simcenter 3D提高专题_术语案例演示4讲之自适应网格划分》和《NX CAE入门与提高(三):NX Nastran网格划分关键技能》。
3. 结论和研讨
5.1 比较和结论
如表1所示为上述悬臂梁同一个模型不同单元类型的单元数量、节点数量、计算结果和误差的对比,其中误差是以理论计算结果(0.2744mm)为基准进行计算的。
表1 不同单元类型计算结果的比较
序号 | 单元类型 | 单元数量 | 节点数量 | 计算结果(mm) | 误差(%) |
1 | 3D/ CHEXA(8) | 152000 | 228456 | 0.283 | 3.13 |
2 | 2D/CQUAD4 | 3200 | 3232 | 0.284 | 3.50 |
3 | 1D/CBAR | 4 | 5 | 0.279 | 1.82 |
上述计算和结果的对比说明:对于模型和截面均为简单的悬臂梁,采用3种不同单元类型计算的结果误差均小于工程应用公认的5%以内,并且在计算这类等截面、长度很长的悬臂梁(包括细长构件)承受纯弯曲受力分析中,采用1D单元计算的精度更为精确,同时大大降低了计算成本,换句话说,分析杆/梁结构为主要特征的复杂模型力学性能,采用1D梁单元来模拟结构,在不失结构真实性的前提下较好地兼顾了计算效率,这正是模型简化和前处理的基本要求。
当然,1D梁单元并不能适合多维度和多结果的工程场合,比如不能用于梁结构承受扭转工况和弯扭组合等受力工况,非等截面梁结构和不规则三维模型的结构分析也无法采用1D梁单元进行仿真计算等等。
5.2 说明和研讨
(1)本文演示的悬臂梁为矩形空心管,如果悬臂梁为实心体,那么分别采用1D/2D/3D单元进行建模和求解,各自的计算结果以及和理论值之间的误差又有何变化呢?同样需要按照上述方法进行实操并进行对比。
(2)在建筑、桥梁等桁架结构以及工程设备中的门架、框架、钢架和网架的受力分析中,往往采用以1D单元类型为主的建模方式便于大大简化模型。如图6所示为润扬大桥南汊桥底下检修装置受力分析的应力云图,该结构由100多根钢制型材组成,总长达到了20m,采用了线框建模和1D单元类型的网格划分进行计算,达到了有限元分析的最佳效果。
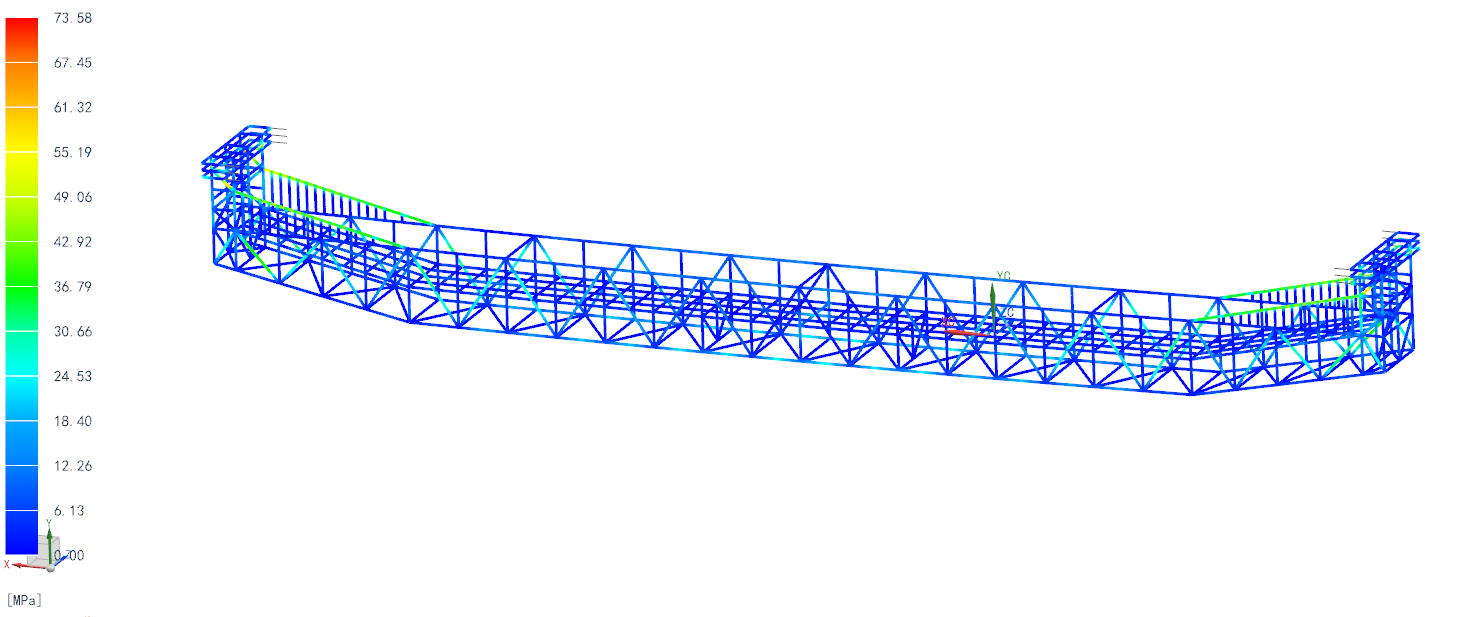
图6 润扬大桥南汊桥检修装置分析云图
(3)简化模型是CAE前处理的必要阶段,对于三维实体零件,采用3D单元来模拟最为真实但最为耗时,因此一些应用场景下可以采取如下的简化处理方法:非回转但结构对称的零件采用拆分体以及进行对称约束来处理;回转零件采用剖分体(一般在ZX平面)并选用2D轴对称单元来处理;旋转叶片类零件采用绕旋转轴剖分N等分并采用循环对称来处理,这些简化和处理都是兼顾求解精度和效率的有效方法。
(4)实际工程中弹簧、轴承、阻尼器和减振器等功能结构,以及螺栓连接、铆接、焊接和粘结等工艺结构也需要选用1D单元形式进行建模和模拟,如果对它们进行2D或者3D单元的网格划分,那么计算成本大大增加,并且有些场合难于实现,也实无必要。
(5)实际工程中很多产品结构是0D/1D/2D/3D各类单元的装配和连接,网格划分后的单元/节点数量达到了百万甚至千万级以上的规模,这类大型数模分析更多的关注是计算效率及其成功率,意味着简化模型和单元降维操作成为了最为关键的前处理步骤。






