ABAQUS:圆柱直齿轮齿根应力校核
“ 由于各类专用传动分析软件在对锥齿轮以及双曲线齿轮的齿根应力计算支持度均不足的原因,就需要使用通用有限元数值计算软件来进行校核。但是使用通用有限元软件究竟该如何得到理想的结果则需要仔细研究。此系列文章将从本文开始,从最简单的圆柱直齿轮开始,使用ABAQUS和KISSSoft进行对标分析,寻找一套鲁棒性良好的分析方法,用于后续的锥齿轮或双曲线齿轮齿根应力校核。”
本文使用的齿轮案例来源于KISSSoft提供的示例文件01 Spur(ISO 6336).Z12。
其基本数据如下图:

其基准齿廓如下图:

01
—
KISSSoft圆柱斜齿轮齿根应力校核
该齿轮对的工作状态如下:
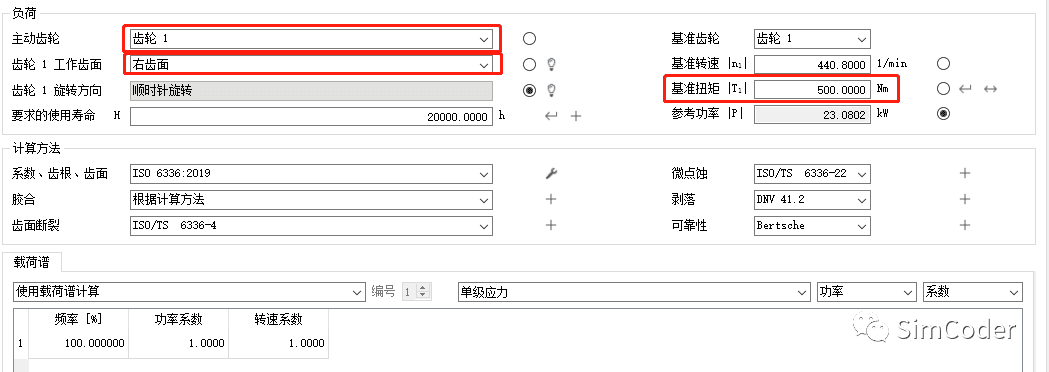
小齿轮为主动齿轮,其右齿面为工作齿面,工作扭矩为500Nm。
接触分析计算齿根应力:
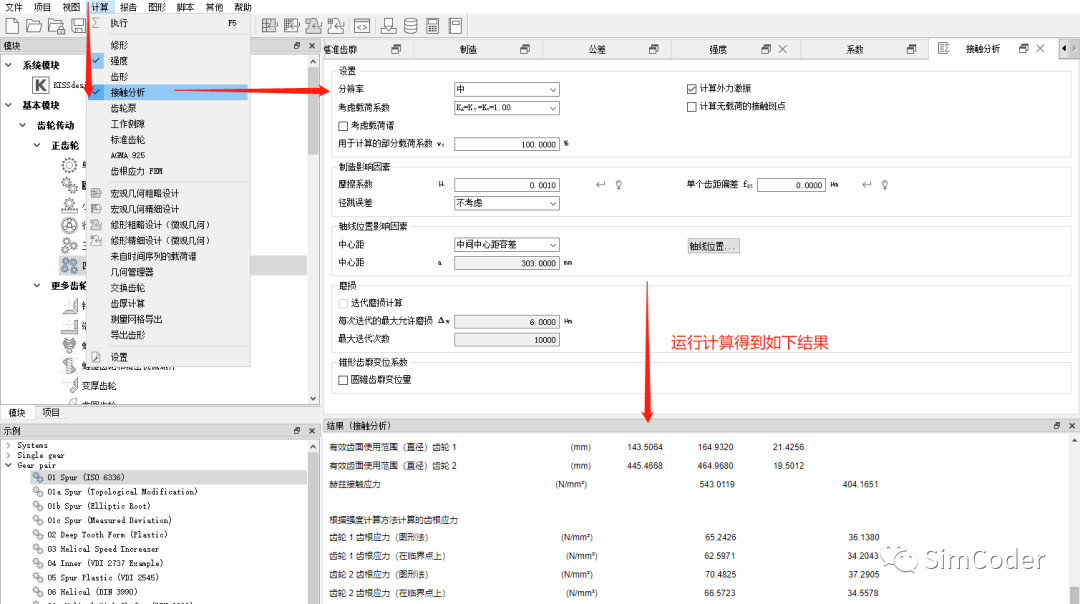
计算得到的最大主应力如下图:
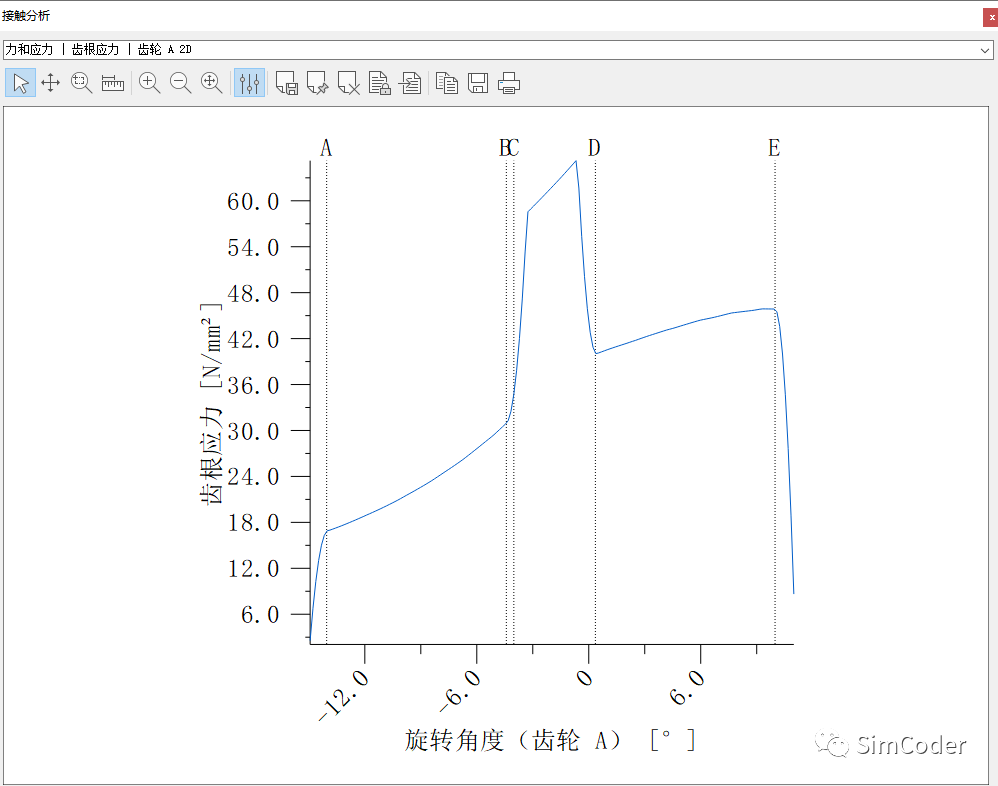
FEM法计算齿根应力:
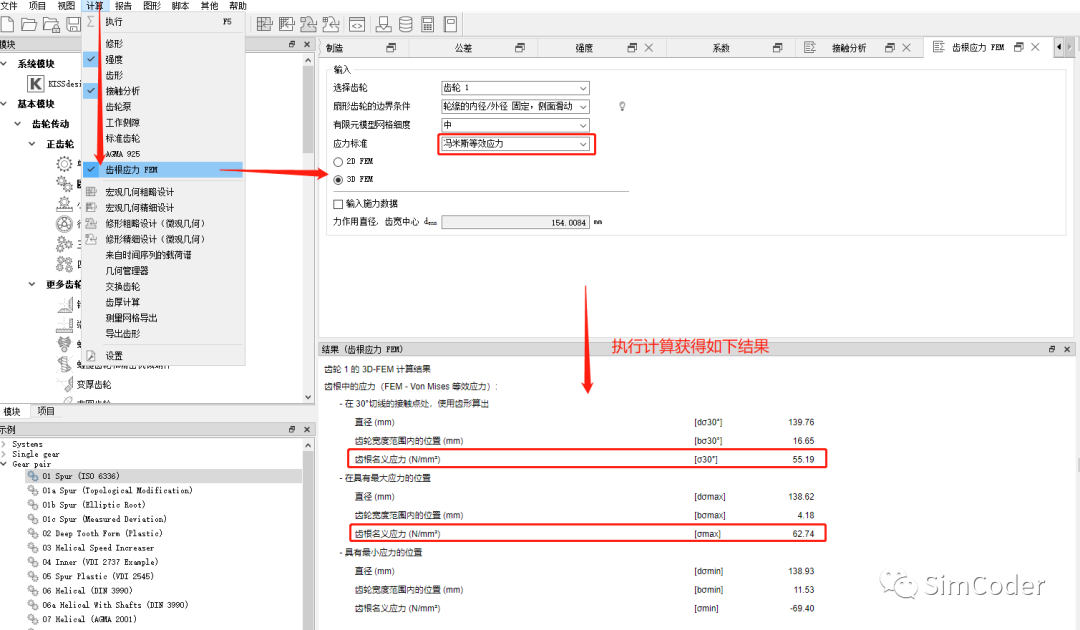
查看最大应力在齿宽方向的分布:
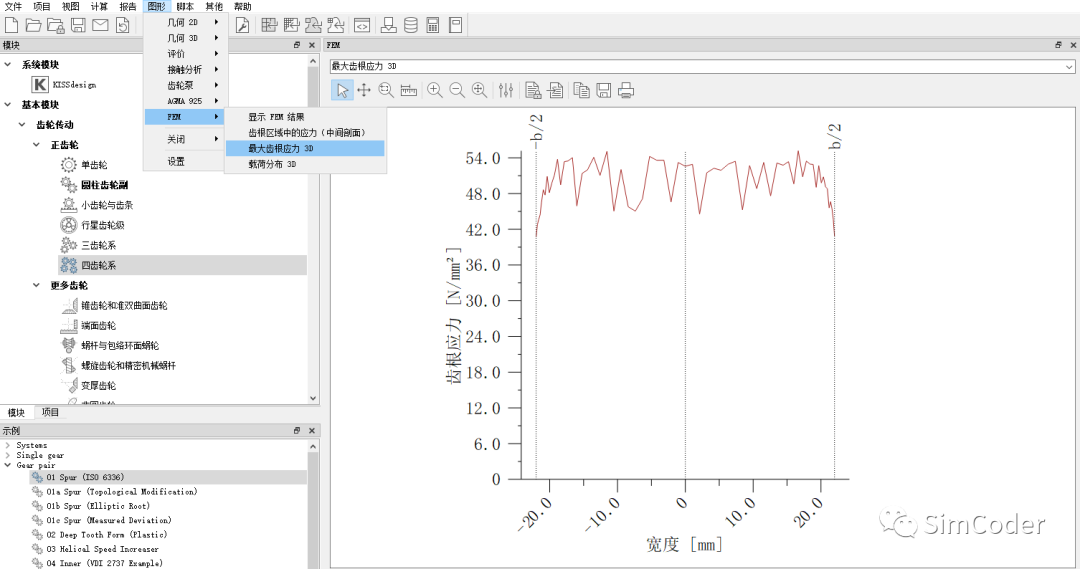
中间剖面的vonMises应力分布:
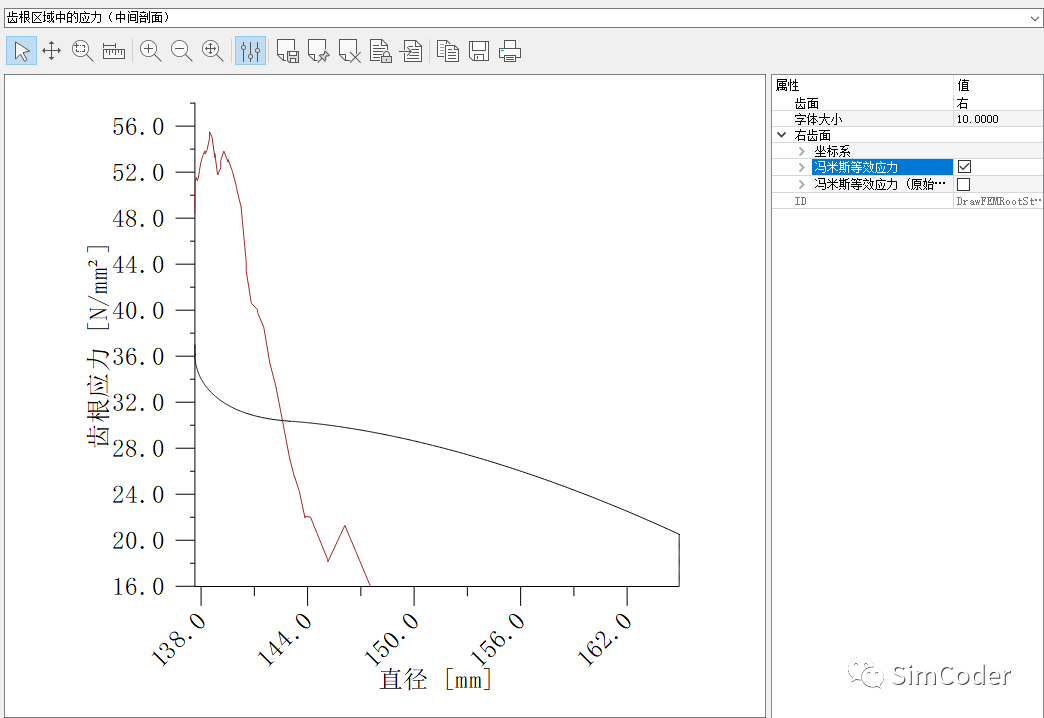
显示FEM结果:

上述两种计算方法得到的结果一致性良好,工作齿面的齿根处最大主应力为65MPa,vonMises应力为55MPa。
02
—
ABAQUS不同单元类型计算齿根应力
ABAQUS中的单元简介:
全积分:当单元具有规则形状时,在数值积分过程中所采用的高斯(Gauss)积分点数目能够对单元刚度矩阵中的插值多项式进行精确积分。“规则形状”指的是单元的边相交成直角,且中间节点位于边的中点。完全积分的线性单元在每个方向有2个积分点,完全积分的二次单元在每个方向上有3个积分点。在承受弯曲载荷作用时,完全积分单元容易出现剪切闭锁现象,造成单元过于刚硬,即使划分很细的网格,计算精度仍然较差。
缩减积分:比完全积分单元在每个方向上少使用一个积分点,因此称为减缩积分。减缩积分单元可以缓解完全积分单元可能导致的单元过于刚硬和计算挠度偏小的问题。如果希望得到的是应力集中部位的节点应力,则尽量不要选用线性减缩积分单元(例如 C3D8R),原因是线性减缩积分单元只在单元的中心有一个积分点,相当于常应力单元,它在积分点上的应力结果是相对精确的,而经过外插值和平均后得到的节点应力则不精确。线性减缩积分单元存在“沙漏模式”(hourglassing)的数值问题,有可能过于柔软。二次减缩积分单元也可能出现沙漏模式问题,但在正常网格中沙漏模式不会扩展出去,如果网格足够细化,就可以保证计算精度。除了大应变的弹塑性问题和接触问题之外,一般情况下二次减缩积分单元是应力/位移问题的最佳选择。
非协调:非协调单元将增强单元变形梯度的附加自由度引入到线性单元中,以避免单元交界处的位移场出现重叠或裂隙。在弯曲问题中,非协调单元的计算精度很接近二次单元的结果,而计算代价远远低于二次单元,但是如果单元形状较差,非协调单元的分析精度会下降。在使用非协调单元时,应在所关心的关键部位分割(partition)出一个形状规则的区域(例如在应力集中部位),在此区域内生成高质量的四边形(Quad)或六面体(Hex)单元网格(各个角尽量为90°),会得到较好的分析结果。
使用结构化网格划分方式,严格把控网格质量,并对齿根处进行网格细化,齿根圆角处划分为8个单元。在分析中为小齿轮指定不同的单元类型(线性、二次,以及相应的缩减积分、全积分、非协调)。

线性缩减积分单元计算结果vonMises:33.92MPa,MaxPrincipal:41.8MPa:

线性全积分单元计算结果vonMises:48.24MPa,MaxPrincipal:50.53MPa:
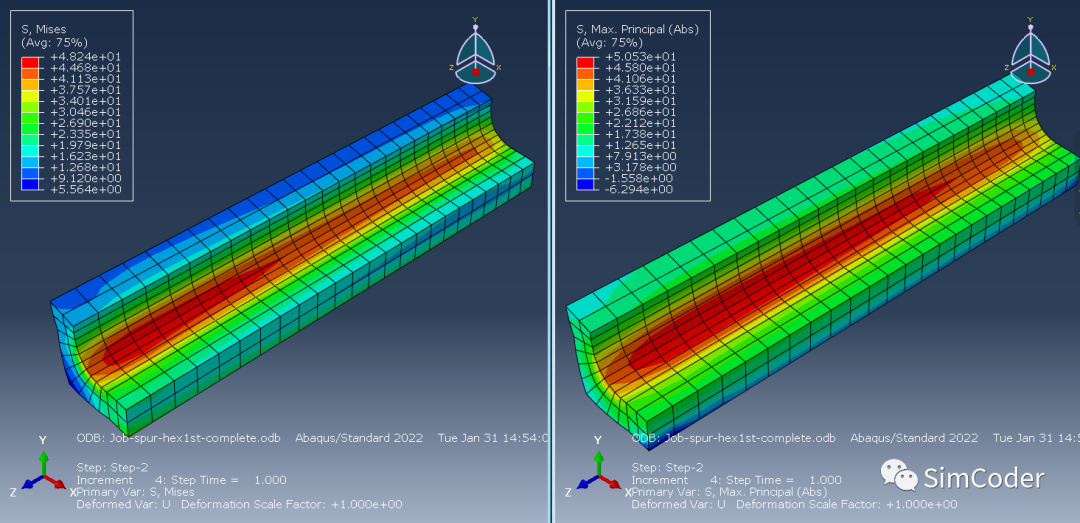
线性非协调单元计算结果vonMises:47.24MPa,MaxPrincipal:57.56MPa:
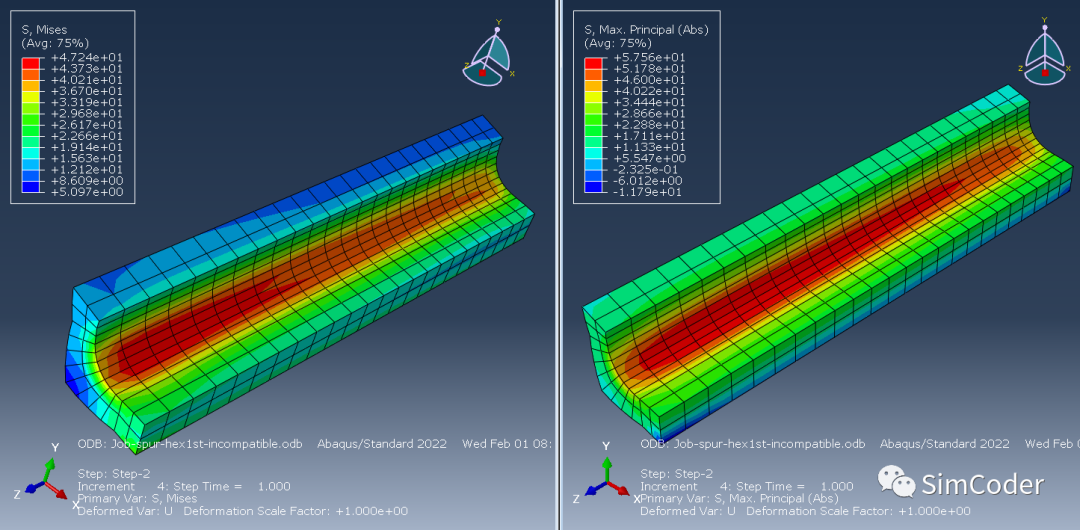
二次缩减积分单元计算结果vonMises:50.59MPa,MaxPrincipal:58.34MPa:
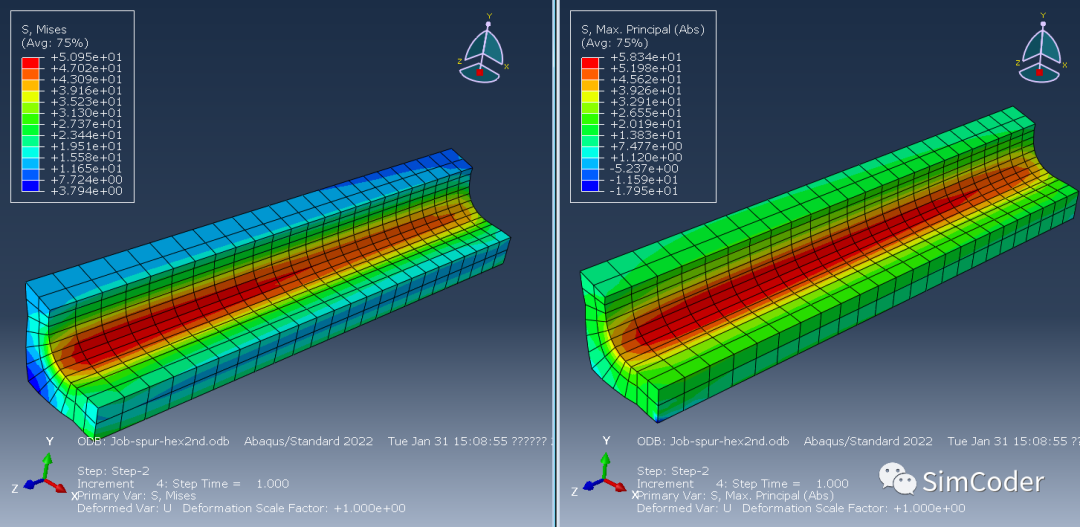
二阶全积分单元计算结果vonMises:54.26MPa,MaxPrincipal:64.9MPa:

从上述分析结果可以看出网格细分程度还有所不足,分析结果受到单元类型的显著影响。
03
—
ABAQUS使用adaptive remesh计算齿根应力
ABAQUS的adaptive remesh可以根据计算结果的应力梯度自动细化网格,当达到设定的收敛值时,完成计算。
使用该功能时,需要将小齿轮的齿面单独切分出来,以避免齿面过高的赫兹接触应力导致计算收敛困难。赫兹接触应力的校核收敛所需的单元尺寸过小,详见ABAQUS:两圆柱赫兹接触应力校核。
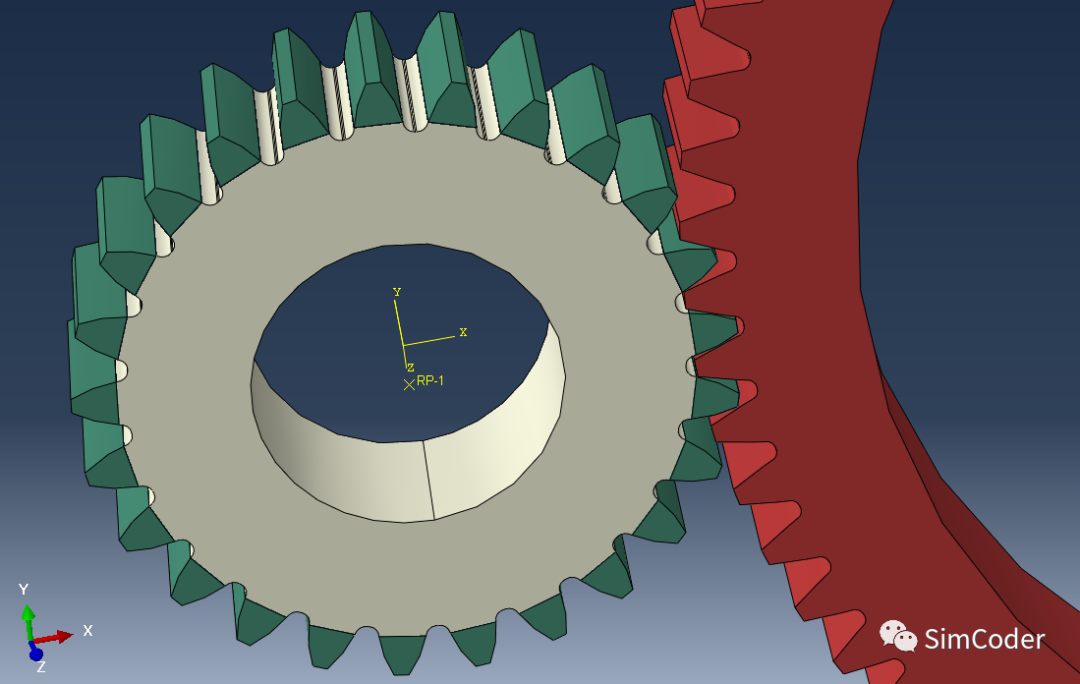
adaptive remesh设置方法:
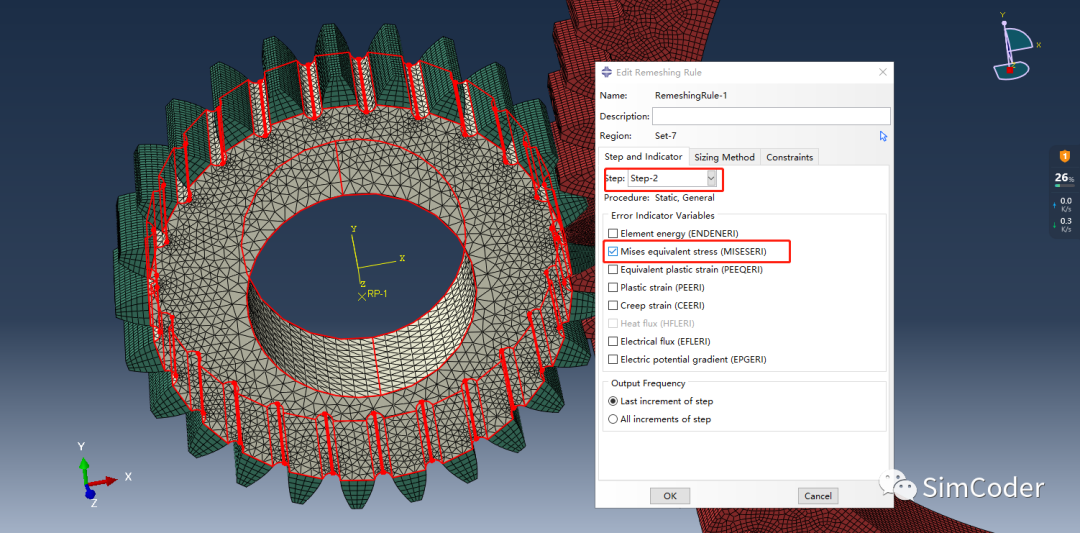
在step 1中,给予小齿轮一个微小的转动角度,以使得接触对生效,step 中正式开始计算,所以我们要指定载荷步为step 2,并且指定收敛指标为vonMises应力。
提交计算:
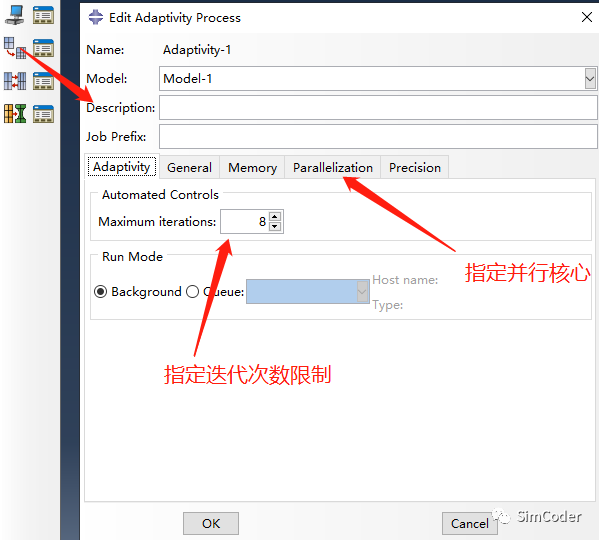
adaptive remesh收敛时计算结果vonMises:56.87MPa,MaxPrincipal:64.47MPa:
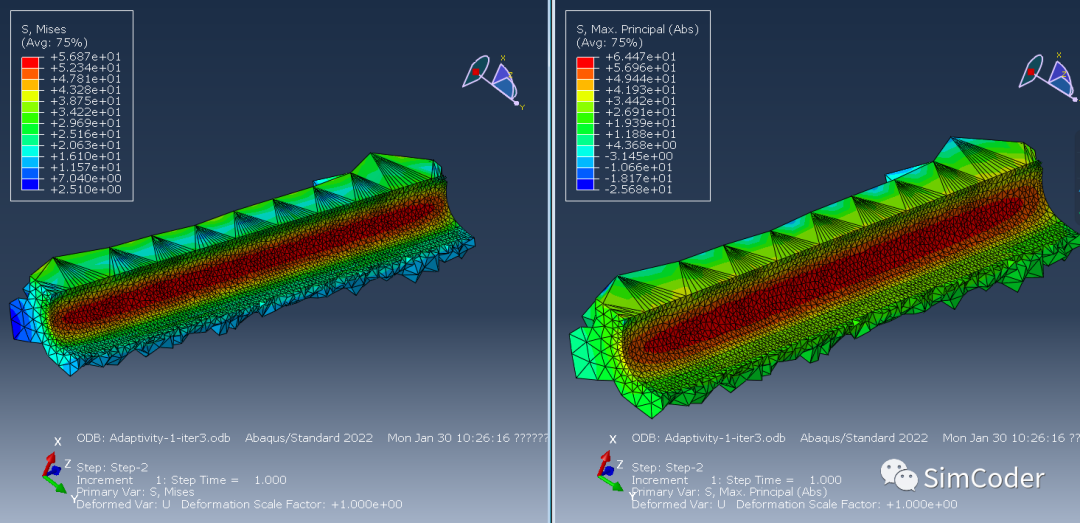
由计算结果可见,其与二阶全积分单元计算结果基本一致。
04
—
总结
| 计算方法 | vonMises应力(MPa) | 最大主应力(MPa) | 备注 |
| KISSSoft | 55 | 65 | 对于简单直齿轮,以此为精确解 |
| ABAQUS线性缩减积分 | 33.92 | 41.8 | 网格不足导致求解结果误差较大 |
| ABAQUS线性全积分 | 48.24 | 50.53 | 网格不足导致求解结果误差较大 |
| ABAQUS线性非协调 | 47.24 | 57.56 | 网格不足导致求解结果误差较大 |
| ABAQUS二阶缩减积分 | 50.59 | 58.34 | 网格不足导致求解结果误差较大 |
| ABAQUS二阶全积分 | 54.26 | 64.9 | 对标效果良好 |
| ABAQUS adaptive remesh | 56.87 | 64.47 | 对标效果良好 |
综上所述,齿轮齿根应力校核对网格密度高度敏感,齿根处8个网格略显不足,需要使用二阶单元全积分才能获得精确的结果。也就是说如果采用线性单元,则需要16个网格才能获得高精度的求解结果。




