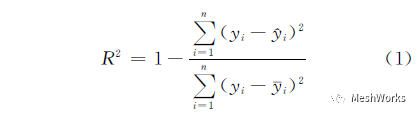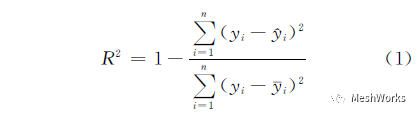基于网格变形技术的车身改型多目标优化
杜倩倩1,陆善彬2
(1.同 济大学 汽车学院 ,上 海201804;2.吉 林大学 汽车工程学院 ,吉 林长春)
摘 要 :文章结合灵敏度分析理论从汽车白车身中筛选出最佳的形状和厚度设计变量,并运用优化超拉丁立方模型构建在设计空间内均匀分布的样本矩阵 ,进而对由网格变形商用软件MeshWorks生成的样本模型进行模拟计算,通过Matlab软件拟合高精度的四阶响应面模型,运用改进的非支配排序遗传算法(NSGA_II)以改型车白车身扭转刚度提升10% 作为约束,以弯曲刚 度和车身质量作为目标进行多目标优化。研究表明,通过网格变形技术建立的形状参数和厚度参数并结合相关的优化理论可以有效地实现车身性能的多目标优化,得到的Pareto最优解集可以在汽车改型设计的初期为设计者提供重要的参考依据。关键词 :网格变形 ;形状优化 ;多目标优化 ;改进的非支配排序遗传算法 ;响应面模型 目前,加快新车型研发进程仍然是现代汽车工程面临的主要挑战之一。新车型的开发方式主要有开发全新车型和基于原有车型进行改型设计2种。后者由于周期短、成本低而被汽车制造商广泛采用。在传统的车身改型设计中,需要反复修改几何模型并将其转换为有限元模型进行分析计算,耗费大量的时间和精力,对设计性能的改进也有较大的局限性。 而运用网格变形技术的汽车改型设计,可以对原有车型的有限元模型进行直接修改,从而方便快 捷地建立各类特征参数(包括厚度参数、形状参数 等),弥补了以 往的车身结构优化多以尺寸优化为主的缺陷,结合计算机辅助工程 (CAE)仿真实验可以对改型车进行多目标的性能优化,一次性获得具有相对最优性能的有限元模型的 Pareto最优解集,从而有效地减少对几何模型的修改次数。设计者可以根据市场竞争车 型的对标结果,并综合考虑市场需求、经济性、工艺性等信息,从 Pareto最优解集中选取相对满意的结 果。最后由计算机辅助设计 (CAD)部门构建几何模型,真正地实现CAE引导汽车设计。 变形技术是将一个给定的二维或者三维物体的几何形状连续、光滑地变成目标几何形状 ,实现两者之间的渐变和过渡[1]。变形技术在几何造型 和计算机动画制作领域中应用较多[2],目前在CAE 领域中主要用于某个结构件的形状、板件厚度和焊点间距等参数的设计改进 ,将其完整系统地用于汽车的改型设计及形状优化[3]的实践还比较少。 文献[4]运用网格变形技术改变白车身有限元模型的形状和尺寸,并成功预测了新车型的性能指标;文献[5]运用网格变形技术对板条轨道的 疲劳寿命进行可靠性设计优化;文献[6-7]运用网 格变形技术对车身的计算流体动力学(CFD)性能进行了优化;文献[8]应用网格变形技术设置车身板件的形状参数, 并对车身性能进行了多目标优化;文献[9]研究了汽车车身结构的多目标优化设计理论;文献[10]通过建立白车身参数化模型 ,针对车身动态和静态性能进行多学科优化;文献 [11]运用神经网络近似模型和非支配排序遗传算法相结合对车身进行多目标优化。 本文以某乘用车的改型设计为例,按照企业要求将整车加宽、加 高、加 长一定的尺寸,再通过网格变形技术对改型车白车身局部结构进行形状和厚度的综合参数化设计 ,并结合四阶响应面近 似模型和改进的非支配排序遗传算法(NSGA_II)对车身的部分静态性能进行多目标优化,所得结果可在一定程度上为初期的汽车改型设计提供重要的参考。1 网格变形实现车身变形
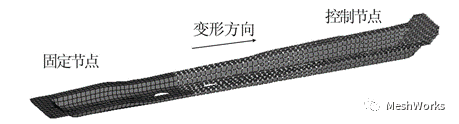
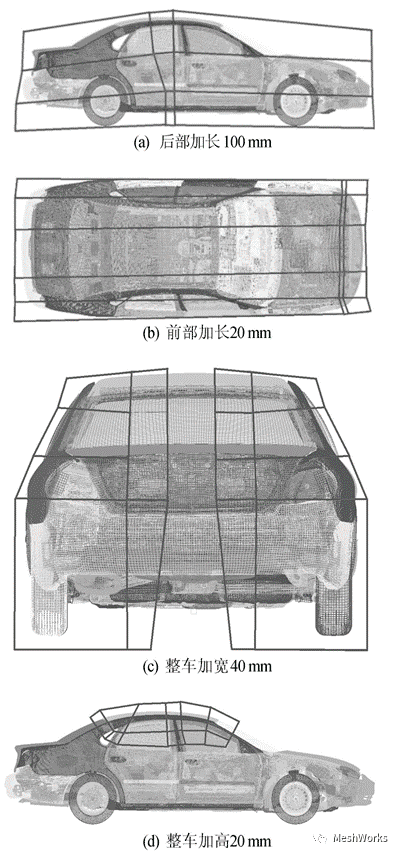
有限元模型的网格变形实质上是以一定表述形式来实现网格节点的运动。其表述形式主要有数学形式和有具体目标形状的几何形式,网格变形技术中的节点可以分为控制节点、可变形节点和固定节点[12]。 控制节点的平移、旋转、缩放等运动可带动可变形节点的运动,从而驱动所需的网格变形。 目前实现网格变形的方法主要有间接控制块方式和自由变形方式2种。间接控制块方式是通过建立至少3个控制块单元包裹并关联变形区域,在相应的控制块单元上选取恰当的控制节点,通过可变形节点和固定节点来实现网格变形,如图1所示。 自由变形方式的网格变形则可根据形状变形要求,直接选取变形区域的网格节点可变形节点 和固定节点分别作为控制节点,并选择合适的变形运动模式和方向,通过光滑变形获得理想的目标形状,如图2所示。商用软件MeshWorks为网格变形提供了较为快捷和友好的操作界面。在基于平台车型的新车型开发模式下,网格变形操作应保证基础车型的白车身主体结构以及车身分块和 焊接关系等特征不发生改变 ,而对车身结构的整 体或者局部结构进行修改,以实现整车的加长、加高和加宽,同时对局部板件形状和板件厚度进行参数化优化设计,以实现基于原有平台车型的系列化设计。 本文中整车的变形是通过间接控制块的方式来实现的,在建立控制块单元时尽量避开主要安装孔的部位,以保证安装匹配要求并减少工艺上的重新开模,降低成本。 根据汽车制造商对新车型的市场定位和竞争车型的整车参数,并综合考虑整 车造型的空气动力特性,本文拟定的变形方案如下:(1)整车加长。 纵梁前端加 长20mm;顶 盖后部,后座椅之前,B柱之后加长100mm。(2)整车加宽。传动轴通道两侧与纵梁之间(不改变主要安装孔的部位)各加长20mm。(3)整车加高。顶盖与 A、B、C柱上端加长20mm。2 改型车白车身静态性能分析
本文主要对改型车的白车身进行板件形状和厚度的参数化设计优化,首先对其白车身静态性能进行有限元模拟分析。 白车身静态性能[13]主要包括车身质量m、白车身弯曲刚度Kw 和扭转刚度 Kn等,其值分 别为 367.1kg、5632.373 N/ mm、14874.039N·m/(°)。 其中,扭 转刚度基本满足要求,而弯曲刚度较小,质量较大,因此本文将白车身质量和弯曲刚度作为优化目标,为了实现车身综合静态性能的提升,将扭转刚度在原来基础上提高10%作为约束。 在实际的工程应用中,考虑到汽车白车身的 模态频率通常在局部结构的改进优化中变化微小,通常先确保车身质量 、弯曲刚度和扭转刚度等达到目标要求后,对优化后的新模型进行模 态频率的验证计算以提高优化效率。因此本文暂不考虑车身模态频率在优化过程中的变化。参数优化设计如下:s.t. 扭转刚度>16361.443N·m/(°);3 灵敏度分析筛选变量
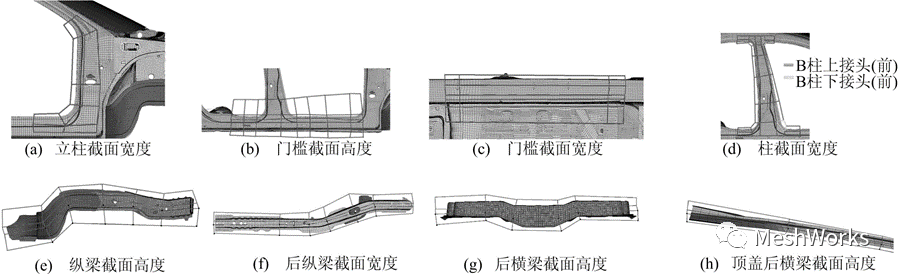
为了减少仿真程序的调用以减少优化时间、 降低成本,因此在进行多目标优化之前运用灵敏度分析的方法筛选出灵敏度较高的设计参数作为设计变量。 根据经验选取20个对车身静态性能有较大影响的形状变量,运 用MeshWorks的网格变形模块建立20个形状参数,用S1 ~S20 表示,其中左右对称的形状参数作为一个参数进行处理,见表1所列。本文车身静态性能对形状变量的灵敏度分析采用的方法是 通过只改变1个形状变 量而保持其他变量不变,统计每个形状变量对关注指标的贡献率来实现的 。分别将每个形状变量沿变形方向移动15mm,计算车身静态性能指标的变化率[14],统计结果见表2所列。本文中车身局部形状的长度、宽度、高度方向分别定义为与车辆坐标系X 轴、Y 轴、Z 轴同向。由表2可知,对 质量贡献较大的是B柱截面长度、门槛截面高度、后纵梁截面宽度、后纵梁截面高度;对弯曲刚度贡献较大的有门槛截面宽度、B柱截面长度、后 纵梁截面宽度、立柱截面长度、 门槛截面高度;对扭转刚度贡献 较大的有后纵梁截面宽度、后纵梁截面高度、后横梁截面长度、顶盖后横梁截面长度 ;B柱上下接头的形状在概念设计阶段为造型设计者提供参考信息。因此共筛选出10个形状参数作为形状设计变量,分别用X1~X10表示,见表3所列。变量的取值范围设为控制节点运动的极限位置,其变形示意图如图4所示。 本文关于厚度变量的筛选是通过Isight软件来完成的。 初步根据经验选取白车身35个板件厚度变量,分别用T1 ~T35 表示。采 用拉丁超立方抽样的方法选取样本点后进行模拟分析计算,根据变量和计算结果进行板件厚度的灵敏度分析,分析结果如图5所示。由图5可得出,对车身质量贡献较大的是T35前围板厚度、T31后纵梁外板厚度、T22纵梁内板厚度和 T17顶盖加强内板厚度、T6B柱内板厚度(对称)、T10门槛外板厚度(对称);对车身弯曲刚度贡献较大的有 T26后地板厚度、T25 前地板厚度、T12侧围板(对称)厚度和T19顶盖后横梁外板厚度;对车身扭转刚度贡献较大的有T12 侧围板厚度、T26后地板厚度、T13地板加强横梁板厚和T31轮罩外板厚度。统计结果后选取12个厚度变量,见表4所列。4 车身质量和静态刚度多目标优化
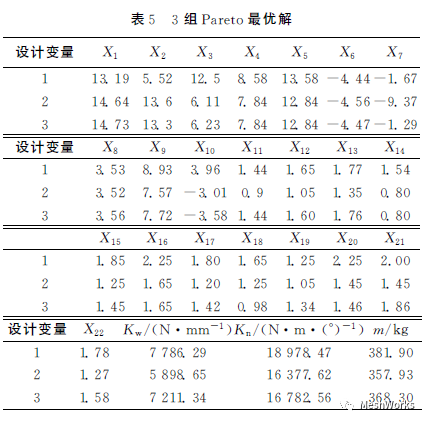
近似模型方法是通过数学模型的方法逼近一组输入变量(独立变量)与输出变量(响应变量)的方法,在工程优化中,运用近似模型仿真可以减少仿真程序的调用,提高优化效率[15]。 本文运用拉丁超立方模型对22个形状和厚度变量抽取 135个样本点,考虑到形状和厚度2种类型的变量与2个目标函数之间响应关系的复杂性 ,因 此建立四阶响应面模型来综合拟合形状和厚度变量与2个目标函数之间的响应关系。它可以较好地逼近复杂的函数关系,具有良好的鲁棒性。本文运用Matlab编程建立四阶响应面模型, 其中形状变量X1对2 个目标函数的响应面模型,如图6所示。响应面模型的拟合精度可用复相关系数的值来检验[15]。复相关系数R2的定义如下: NSGA_II算法的基本方法是由当代父代群体进行交叉和变异得子群体,并将2个群体合并[16]。将获得的新群体按照目标函数的Pareto最优关系两两进行比较后产生多个依次控制的前沿层。属于不 同 的 Pareto层 的个体可通过评价 Pareto优越性来评价个体的优劣;属于一个Pareto层的个体可利用NSGA_II中导入的拥挤距 离和拥挤距离排序的方法对个体进行排序,具有更大的拥挤距离的个体更优秀[16]。NSGA_II在非支配排序中,接近Pareto前 沿 的个体才被选择,使Pareto前进能力增强。 本文针对车身刚度和轻量化的多目标优化数学表达式如下: 本文中设置NSGA_II的种群规模为100,进 化代数为100,交叉概率为0.8,变异概率为 0.1。 获得的 Pareto前沿如图7所示。 得到的Pareto最优解集中共有40组最优解,其中3组见表5所列。由图7可以看出,由NSGA_II获得的Pareto前沿的连续性和均匀性都比较好 ,其一个Pareto最优解需要2.8次评价,寻优效率较高。对Pareto最优解集进行分析得出:在比原改型白车身扭转刚度提高10%的约束下,得到的 Pareto最优解 集中,最大弯曲刚度为7786.29N/mm,相对于变形前的5632.373N/mm增加了38.24%,最大扭转刚度为18978.47N·m/(°),比原来增加了27.59%,对应的质量为381.9kg,比原来的367.1 kg仅增加4.03%,最小弯曲刚度为5898.65N/mm,至少提高4.73%,最小的扭转刚度为16377.62N·m/(°),比原来增加10.11%,对应的质量为357.93kg比原来减轻2.5%,因此,本文的优化效果是较为显著的。本文对由NSGA_II算法得到的Pareto最优解集中的部分最优解运用MeshWorks生成优化模型进行了有限元仿真计算,检验得到的最优解与仿真值的相对误差均在10%以内。为保证改型车的白车身具有良好的动态性能,本文对生成的Pareto最优解集的CAE模型进行了模态仿真验算,结果是一阶弯曲频率均为30.92~31.56Hz,一阶扭转频率均为46.51~47.86Hz,相对原平台基础车型变化较小,基本满足动态性能要求。从而证明了该优化方法的有效性和可行性。5 结 论
本文通过网格变形技术结合多目标优化理论系统高效地实现了汽车的改型设计,车身的静态性能均有较大的提升。 车身弯曲刚度可以提升4.73% ~38.24%,车 身扭转刚度可以提升10.11%~27.59%,车身质量的变化范围为 -2.5%~4.03%,优化效果较为显著。在实际的工程应用中,设计者可以根据改型车的市场定位信息并综合权衡车身弯曲刚度、扭转刚度和轻量化的比重,从Pareto最优解集中选取合适的CAE模型。 与传统的经验式改型设计相比,基于网格变形技术的汽车改型设计方法具有周期短、成本低的显著优点,在实际的工程应用中具有重要的指导意义。 网格变形技术为形状优化开辟了新途径,与尺寸优化相结合可获得更显著的优化效果。著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-01-31
最近编辑:1年前