李英华:基于应变监测数据的大跨度连续刚构桥的可靠性评估( in English)
Author:Li Yinghua
Abstract
when to do bridge maintenance and which individual component of the bridges needing maintenance is a world problem at present, and the health monitoring system is considered to a very helpful tool for solving this problem. As the continuous monitoring over a long-term period can increase the reliability of the assessment, so, a large number of strain data acquired from the structural health monitoring system (SHMS) installed on a long-span prestressed concrete continuous rigid frame bridge is adopted in this paper. Firstly, a calculation method of point time-dependent reliability is proposed based on the basic reliability theory, and introduced how to calculate reliability of the bridge by using the stress data transformed from the strain data. Secondly, combined with “Three Sigma” principle and the basic pressure safety reserve requirement, the critical load effects distribution function of the bridge is defined, and then the maintenance reliability threshold for controlling the unfavorable load state which appears in the early operation stage of this type bridge is suggested. Finally, the advantages and drawbacks of the methodology suggested in this article are discussed. To sum up, the method can help bridge engineers do effective maintenance of the bridges.
Keywords
structural health monitoring; point time-varying reliability; the critical load effects distribution function; maintenance reliability threshold; continuous rigid frame bridge; “Three Sigma” principle
1. Introduction
In the world, people have recognized the importance of the SHMS for monitoring large-span bridges during in construction and service. At present, the health monitoring system becomes an indispensable part of long-span bridges, of which the role is to supply safety evaluation of bridge construction and operation (Muria et al. 1991, Cheung and Tadros 1997, Curran and Tilly 1999, NIuadi 2002, Cheung and Naumoski 2002, Mufti 2002, Wong 2004, Chan et al. 2006, Simon 2011, Li et al. 2014). Due to many influence factors of the data collected from the SHMS, such as: environmental factors, large size of the data itself, instability of material properties and the structure shape, load and resistance changing with time during the bridge operation etc., therefore, it makes to evaluate the bridge safety and help do effective maintenance in bridge operation by the data collected from the SHMS very difficult.
At present, many international experts and scholars have done effective work in the area of using the information from SHMS for rational maintenance planning of deteriorating structures. Thoft-Christensen (1995) proposed to apply reliability theory in bridge management systems. The international workshop (Frangopol et al. 1996a, 1998b) on structural reliability in bridge engineering has demonstrated the advantages of using reliability based methods in the key field of civil infrastructure systems. Frangopol (1999) developed the basis for cost-effective bridge management incorporating lifetime reliability and life-cycle cost. Frangopol and Das (1999) and Thoft-Christensen (1999) defined the bridge reliability states and proposed a reliability-based approach to bridge maintenance, and suggested the maintenance reliability threshold of the steel- concrete composite bridge to take the value 4.6 based on theory and experience. Dan M. Frangopol (2001) systematically concluded the birth and growth of bridge management systems, and suggested that the limitations of current bridge management systems could be overcome by using the reliability-based approach. Dan M. Frangopol et al (2001) suggested that the limitations of bridge management systems can be overcome by reliability-based method. K.J.M. et al (2005) suggested an idea of calculating the bridge reliability by using the basis reliability theory and the stress monitored data. F. Akgul and D. M. Frangopol (2005) explored the general methods for the analysis of the bridge performance in the life cycle and applied their research achievements in more than a dozen concrete bridges located in American Crow Leader states. M. G. Stewart and J. A. Mullard (2007) proposed a space and time related reliability analysis method to predict the probability of crack and damage degree under environmental erosion in concrete bridges. Mustafa Gul and F. Necati Catbas (2009) investigated the statistical pattern recognition for SHMS by using time series modeling of theory and experimental verifications. Sunyong Kim and Dan M. Frangopol (2010) provided an approach for cost-effective monitoring planning of a structure system based on a time-dependent normalized reliability importance factor (NRIF) of structural components. André D. Orcesia and Dan M. Frangopol (2011) researched the optimal maintenance strategies based on monitoring information and shown the benefits of SHMS. Helder Sousaa et al (2013) did long-term prediction of prestressed concrete bridges based on monitoring data, and discussed the differences between the measurements and the results obtained with the numerical model, namely the trends due to shrinkage and creep and the variations due to the temperature. Liu Yuefei et al (2014) adopted the Bayesian dynamic models (BDMs) to predict the structural load effects based on the monitored data (everyday monitored extreme stresses) and predicted the structural reliability indexes with First Order Second Moment method (FOSM).
To sum up, there is little monitoring data of SHMS for the assessment of bridge safety at the time, and the bridge maintenance strategy by the use of SHMS during operation is mainly based on expert experience and theoretical analysis at present. Therefore, in this paper, combined with large amount of strain monitoring data of a bridge SHMS and “Three Sigma” principle, a new methodology of calculating reliability and determining maintenance reliability threshold for the concrete continuous rigid frame bridge in early operation stage is presented. This method is useful for bridge engineers to do bridge maintenance.
2. The main idea of reliability calculation based on strain monitoring data
2.1 Calculation method
According to the method adopted by J. M. Ko et al. (2005), the failure probability Pf (or safety index β) of the structural components can be evaluated by means of considering both the member resistance R and the load effects S as random variables and can be written as:

In the formula: fR(r) and fs(s) are the probability density functions of R and S .
If fR(r) and fs(s) both obey normal distribution respectively, the calculation formula of the reliability index can be written as:

In the formula: Φ-1 is the inverse function of the standard normal distribution; μR and μs are the mean of the resistance and load effects respectively; σR and σs are the standard deviation of the resistance and load effects respectively.
2.2 The probability density function of the structure resistance
For concrete bridges, the concrete strength probability distribution function is taken as the probability density function of the resistance R , which generally obeys Gauss distribution and can be obtained by in situ material tests. As the tensile and compressive properties of concrete are different, two equations are adopted to represent the compressive and tensile strength distribution function:

In the formula: fRc(r)and fRt(r) are the Gauss distribution function of the compressive and tensile strength of concrete respectively; μc is the mean of the compressive strength of concrete; σ2c is the variance of the compressive strength of concrete; μt is the mean of the tensile strength of concrete; σ2t is the variance of the tensile strength of concrete. The mean compressive strength μc of concrete material is got by in situ test in this article. As for the variance σ2c , according to the highway reinforced concrete and prestressed concrete design specification JTG D62-2004 (2004), the variation coefficient can take δf=0.11 , and then the variance σ2c of the compression strength of concrete used in the bridge can be got. In this paper, the compressive strength mean and standard deviation of the concrete used in the bridge for a case study (seen in section 3) can be acquired, seen in Table 1.
According to the specification (2004), there is a relationship between the mean axial tensile strength of the concrete used in the bridge member and the mean standard cube compressive strength:

On the above, it has been written that the mean compressive strength can be obtained by in situ test. Therefore, the concrete member axial tensile strength μft can be got by the above formula (4). Also, according to the variation coefficient δf suggested in the specification (2004), which can take the value 0.11, then, the variance σ2t of the axial tensile strength of the concrete can be acquired. Therefore, the tensile strength mean and standard deviation of the concrete used in the bridge can be got, seen in Table 1.
Table 1 The mean and standard deviation of the concrete compressive and tensile strength

In fact, due to the durability and fatigue and other factors, concrete strength changes over time. D. T. Niu et al (1995) statistically analyzed the test results of long-term exposure concrete and in-service structures, and the results showed that concrete strength still subjected to normal distribution, but its mean and standard deviation changed, and the time-varying model of concrete cube compressive strength under the general atmospheric environment were given by

In the formula: μfcu0 and σfcu0 are the mean and standard deviation of cube compressive strength of concrete (28 days curing) respectively; μfcu(t) and σfcu(t) are the mean and standard deviation functions of the compressive strength of concrete cubes respectively after t years service.
However, Eq. (5) is mostly applied for building structures which mainly bear static loads, and the main factor that affects the strength of concrete in Eq. (5) is the durability of concrete. As for bridge structures, live load effects is also quite significant. In addition to the factor of durability, the material fatigue can also cause concrete strength decay, and its effect can not be ignored in practical engineering. J. L. Zhang et al (2004) tested the concrete strength of more than 10 old bridges located in the Central South and the South China regions by means of hammer, core samples drilled and ultrasonic wave methods, and 703 useful data were obtained, and modified Eq. (5) based on the obtained data, and suggested the formula for concrete bridges given by
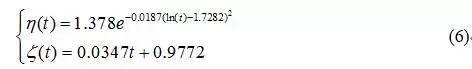 In fact, Eq. (6) is revised by means of the bridge structure in situ measured data, which is under the dual roles of durability and fatigue and close to the actual bridge structure conditions. As the bridge adopted in this article lacks actual traffic statistical data and it also located in South China’s Pearl River Delta region, Eq. (6) is so adopted here to revise the resistance R in Eq. (1).
In fact, Eq. (6) is revised by means of the bridge structure in situ measured data, which is under the dual roles of durability and fatigue and close to the actual bridge structure conditions. As the bridge adopted in this article lacks actual traffic statistical data and it also located in South China’s Pearl River Delta region, Eq. (6) is so adopted here to revise the resistance R in Eq. (1).
As for the changing law of concrete tensile strength, combined with Eq. (4) and Eq. (6), this paper suggests:

In the formula: μt0 and σt0 are the mean and standard deviation of concrete cube tensile strength under 28 days curing respectively; μt(t) and σt(t) is the time-varying equations of the mean and standard deviation respectively after the concrete cube services t years.
2.3 Structural load effects probability density function
K. M. Jo etc. (2005) assume that the bridge load effects probability density function also obey normal distribution. So, the load effects probability density function can be expressed as the following formula:

In the formula: fs(s) is the Gauss distribution function of the concrete member load effects; μs is the component load effects mean; σ2s is the component load effects variance.
According to the previous discussion, the resistance and load effects of the bridge are both obey normal distribution. Therefore, the reliability of the concrete bridge can be calculated according to Eq. (2).
Because the bridge member resistance has two probability density functions fRc(r) and fRt(r), therefore, according to Eq. (1), there are two reliability indexes βc and βt responding to the load probability density function fs(s) . In view of this, the calculation methodology in this paper is: if |μs-μc|>|μs-μt|, calculate reliability index βc according to Eq. (2); if not, then, calculate the reliability index βt , of which the meaning is shown in the calculation schematic diagram below:

Fig. 1 Reliability index calculation schematic diagram of the prestressed concrete bridges
Then, as the reliability index calculated by the above proposed methodology only reflects the local reliability state and the time-varying characters around the embedded sensors, so, we call this point time-varying reliability.
3. Illustration of the SHMS of the bridge used in this article and initial data processing
3.1 The long-term heath monitoring system installed on the bridge
The superstructure of the bridge main beam is a continuous box-beam system with a total of eight main piers and 7 main spans. The first span is 145.4 m long and the sixth span is 87 m long, and the 4 center spans are all 144 m long. The cross section of box girder is a single-box and single-chamber. The heights, thickness of base plate and thickness of web plate vary from 8 m to 2.8 m, 1 m to 0.32 m and 0.9 m to 0.45 m respectively in cross sections from the supporting base to the mid-span.
The cross sections with the measuring points of the health monitoring system in girder locate near piers, in mid-span and in 1/4 span, and there are total 20 sections. The embedded locations of strain variety sensor (The sensor is show in Fig. 2) in each section are illustrated in Fig. 3 with given numbers. With the given name of cross section and number, a sensor in the SHMS can be located in the girder uniquely, such as a sensor is named 3-4MID-1, which means it locates in the top plate center of the mid-span cross-section between pier 3# and pier 4#. The measuring time interval of each sensor is 1 hour. The parameters of JMZX-215 type strain gauge are shown in Table 2. So far, monitoring of the bridge is still continuing and data for the past few years has been acquired.
Table 2 Basic performance parameters of JMZX-215 type strain gauge


Fig. 2 JMZX-215 intelligent string-type digital strain gauge installed inside the bridge before casting

Fig. 3 Positions of the embedded sensors in bridge cross section
3.2 The initial monitoring data
At present, the bridge has been monitored more than 4 years. Here, the data collected from the sensors named 3G1H-1, 3-4MID-1, 4Z9H-1 and 3-4MID-2 are selected as examples, of which the selected monitoring time range is from March 2006 to April 2010. In fact, there are tens of thousands of data collected from the health monitoring system. The monitored data should be pre-processed firstly to delete some singular values which may be induced by strong thunders and other unexpected factors. The principle of deleting the singular values is: firstly, find out the difference between the values of each sampling point and its previous sampling point; then, if the value of the difference is greater than 200 micro-strains (engineering experience value (2007)), the signal value of this sampling point is regarded as singular value and will be removed. Fig. 4 shows the shape of the original data after the singular values are deleted.

Fig. 4 The data profile collected from the SHMS
3.3 Processing of the strain data
As the monitored strain can not be directly used for reliability calculation, it must be carried on some necessary processing to transform into stress, and then can be used to calculate the reliability index. The steps are as follows:
(1) Take the sensor initial setting value after the casted concrete is solidified. Because the sensors are embedded before the concrete casting, the concrete hydration heat will produce initial strain in sensors. So, this value should be subtracted from the monitored strain value of each sensor, of which the goal is to get setting values of the sensors after the concrete is solidified.
(2) Subtract the shrinkage and creep strain values from the sensor monitoring strain value. By use of the finite element technology, build simulation model of the bridge according to each construction stage until to the bridge closure (For example, use finite element calculation software MIDAS etc.), and modify the finite element model by the field test data. Then, based on the FEM model of the bridge, calculate and extract the shrinkage and creep values corresponding to the embedded sensor position. Then, subtract this value from the sensor measuring strain values.
(3) Subtract the thermal expansion strain value from the sensor monitoring strain value. Due to the variation of environmental temperature, the monitored strain values include thermal strain. It is best to choose temperature digital strain senor, as mentioned above, which can simultaneously monitor temperature. So, it is easy to remove the thermal strain from the monitored strain.
After the monitored data is processed according to the above method, the stress data can be conversed from the strain data by the following formula:
![]()
In the formula: E is the concrete elastic modulus.
In case of a limited number of measurements of SHMS, Bayesian methodology (2014) can be used to update the structural resistance and load effects. Nevertheless, continuous monitoring over a long-term period can increase the reliability of the assessment and prediction of structural performance. In general, the damage development speed of bridges is very slow. Considering this reason and the data sample size etc., this paper determines each statistical time section of the monitoring data is 6 months, and so the data sample size of each statistical time section will reach 4000, which is enough for load effects statistics, and the derived load effects include the influence of environmental temperature (include extreme weather), the structure shape, the traffic loads (include heavy loads) and resistance changing with time during the bridge operation etc.
According to the climate characteristics of the bridge which locates in Chinese Pearl River Delta area, then, the time statistics section has two kinds: one is called summer section, from May to October; another is called winter section, from November to April of the next year. In this paper, the statistical time starting point is 2006 May and the end point is 2010 April, and each statistical time section is named in a series A, B, C, D, E, F, G, H.
4. The maintenance reliability threshold determination during bridge early operation stage
4.1 Example analysis
Take the data collected from the sensor named 2-3MID-2 embedded in the mid-span section base plate between 2# and 3# pier of the bridge for example, process the data according to the method suggested in Section 3.3, convert the data into stress data, and then do statistical analysis of the stress data and deal with the statistical data by Gauss distribution fitting, which can be seen in Fig. 5.
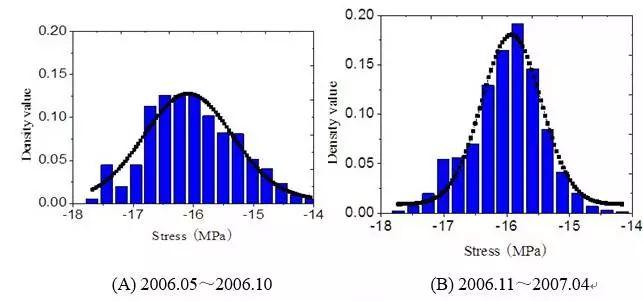

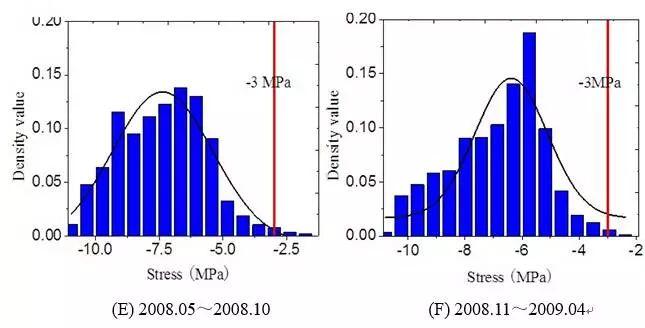

Fig. 5 Stress distribution statistics and Gaussian distribution fitting
Through the above statistics analysis of the converted data, the mean and standard deviation of the measured load effects probability distribution can be obtained for each time section, of which the standard deviation is shown in Table 3:
Table 3 The standard deviation of the measured load effects probability distribution in each time section

As can been seen in Fig. 6, the load distribution function fs(s) is gradually close to the tensile strength distribution function fRt(s) . Therefore, this paper only calculates βt. Based on the method suggested in Section 2, we can get the point time-dependent reliability around the embedded position in the bottom plate in the mid-span cross-section, which is illustrated in Fig. 6. Fig. 6 shows that the reliability βt reduced significantly when the bridge was in service about a year’s time. Fortunately, it remains stable a year later. The reason may be that the early concrete shrinkage and creep, prestress loss and other factors are not calculated precise enough.

Fig. 6 The reliability change over time which is calculated by
4.2 Brief introduction of “Three Sigma” principle
Since the last twentieth century, the human productivity continuously develops, and the product and quality are continuously improved. In twenty-first century, the quality becomes the theme of the new century. There is firstly “Three Sigma” principle in quality management in the past, and now “Six Sigma principle” is suggested. At present, the procedure guarantee capability and management level of the majority enterprises (Including construction enterprises) in the world is in the range about “Three Sigma” to “Four Sigma”.
“Three Sigma” principle itself is generated from normal distribution of the statistics. The normal distribution is determined by two important parameters: the mean and standard deviation. In total quality management, there is:
![]()
The above formula shows that the probability of the quality characteristic values falling without the confidence interval (μ-3σ ,μ+3σ ) is only 0.27%.
Bridge construction project is inherently a planned or under construction building products, and obsess the same quality connotation with other products, namely a set of natural characteristics to meet the need, which includes: safety, adaptability, reliability, economy and environmental suitability etc, of which the main influence factors are: the human factors, technical factors, management factors, environmental factors and social factors etc. Therefore, the idea of total quality management can also be applied on the bridge from design, construction, operation, to maintenance.
4.3 The calculation of maintenance reliability threshold for the bridge early operation stage
Generally, the modern large-span continuous rigid frame bridge construction is under monitoring, and so the failure probability or reliability index of the components or the cross-section can be obtained by the above method. Frangopol (1999) put forward 5 kinds of bridge reliability status, and assume that the bridge life can be seen as a reliable state process from the intact (β≥9.0) to the unacceptable (β<4.6). However, Frangopol just suggested the maintenance reliability threshold 4.6 of the steel-concrete composite bridge according to theory and experiences. As for this problem, combined with the monitored data, this paper puts forward a method to determine the maintenance reliability threshold of the prestressed concrete bridge during early operation stage.
As can been seen in Fig. 5, the stress state of the mid-span base plate is gradually changed from compression to tension, and then the pressure safety reserve become small. Seen from Fig. 5 (d) – (g), there is compressive stress between 2 ~ 3MPa of the unfavorable load state which is unfavorable on the bridge, which means that the pressure safety reserves is too low and is inconsistent to the general engineering experience request that the pressure safety reserve is at least 2 ~ 3MPa under the most unfavorable load conditions.
According to the above description in Section 4.2, at present, the procedure guarantee ability and management level of most enterprises in the world are about in the range from “Three Sigma” to “ Four Sigma”. Therefore, this paper adopts “Three Sigma” standard management level to determine the maintenance reliability threshold of the bridge. According to the request that the pressure safety reserve is at least 2~3 MPa under the most unfavorable load condition, this paper takes the value 2 MPa. Then, the bridge maintenance reliability threshold is calculated as follows:
Firstly, according to “Three Sigma” standard and the minimum 2 MPa pressure safety reserve requirement, this article defines a critical load effects distribution function for calculating the maintenance reliability threshold, and the calculation diagram is shown in Fig. 7, in which we only consider the probability of the abnormal load effects fall in the right confidence interval [ -2MPa,+∞ ], and the reason is: taking into account the compressive properties of the concrete, the probability of the abnormal load effects which does not comply with the design requirements falling in the left confidence interval [-∞,μ-3σ ] is too small and can be basically neglected. Among them, the critical load distribution function standard deviation σth is obtained by the monitored data, and this paper takes the mean σth=1.388 from Table 3 in Section 4.1. So, based on Fig. 7, we can get the critical load effects distribution function mean which is μth=-5.86MPa.
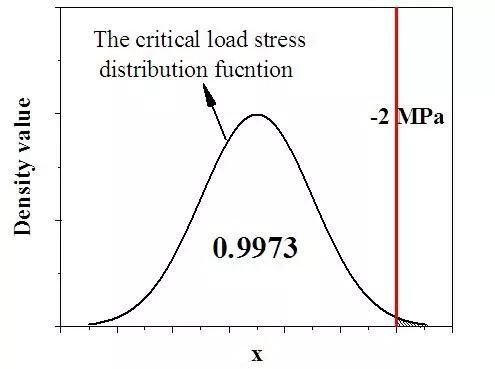
Fig. 7 Diagram of the determination of the critical load effect distribution function
Secondly, based on the mean μth and standard deviation σth of the above determined critical load effects distribution function, use the mean and the standard deviation of the tensile strength shown in Table 1, combined with Eq. (2), we have calculated and find the corresponding critical reliability value βtth=6.13 , and this value is taken as the maintenance reliability threshold of the bridge.
Actually, the maintenance reliability threshold is calculated by the concrete early tensile strength parameters when the bridge is in early operation. Therefore, the maintenance reliability threshold suggested in this paper is mainly aimed at the regulation of the early appeared unfavorable internal force state because of the early concrete shrinkage and creep, prestress loss etc.
However, the critical reliability value βtth=6.13 should be revised, of which the main reason is that the traffic loads of each bridge is different and so leads to Eqs. (5), (6) and (7) not precise enough.
5. Conclusions
As for the difficulties of the bridge maintenance strategy, based on the monitoring data collected from The SHMS of a prestressed concrete continuous rigid frame bridge, this paper put forward a kind of this type bridge point time-varying reliability and early operation maintenance reliability threshold calculation methodology, and the main conclusions are as follows:
● The monitoring data shows that the load effects of concrete bridges basically obey Gauss distribution, and so we can use Eq. (2) for reliability calculation.
● Based on “Three Sigma” management principle and the strain monitoring data, the critical load effects distribution function of this kind bridge is suggested in this manuscript.
● By the basis reliability theory and the above determined critical load effects distribution function, the early operation maintenance reliability threshold 6.13 of the prestressed concrete continuous rigid frame bridge with C50 strength grade concrete is recommended. Of course, the suggested reliability threshold should be revised by actual traffic loads statistics.
● The next stage research should focus on the bridge maintenance reliability threshold study after the bridge is in long-time operation, which is in order to develop maintenance strategy of replace, repair, and reinforcement of the bridge components due to the bridge material strength degradation.
The method suggested in this paper can provide a reference for bridge engineers doing rational bridge maintenance in operation.
Acknowledgements
During the research, Dr sun provide help for the article. So, the first author is very grateful for this.
References
Akgul F., Frangopol D. M. (2005), “Lifetime Performance Analysis of Existing Reinforced Concrete Bridges”. J. INFRASTRUCT SYST., 11(2) , 122-128.
André D. Orcesia, Dan M. Frangopol. (2011), “Optimization of bridge maintenance strategies based on structural health monitoring information”. STRUCT. SAF., 33 (1) , 26–41.
Cheung M. S., Tadros GS (1997), “Field monitoring and research on performance of the confederation bridge”. J. CIV. Eng., 6 (24), 951-962.
Curran P., Tilly G. (1999), “Design and Monitoring of the Flintshire Bridge”. STRUCT. ENG. INT., 3 (9), 225-228.
Cheung M. S., Naumoski N (2002), “The first smart long-span bridge in Canada—health monitoring of the Confederation Bridge”. Proceedings of the 1st international workshop on structural health monitoring of innovative civil engineering structures, Winnipeg, ISIS Canada Corporation.
Frangopol D. M., Hearn G., etc. (1996a), “Structural reliability in bridge engineering”. McGraw-Hill, New York.
Frangopol D. M., Ghosn M., Hearn G., and Nowak A. S. (1998b), “Structural reliability in bridge engineering”. J. Bridge Eng., ASCE, 3(4), 151–154.Frangopol D. M. (1999), “Bridge safety and reliability”. ASCE, Reston, Va., 210–236.
Frangopol D. M., Das P. C. (1999), “Management of bridge stocks based on future reliability and maintenance costs”. Current and future trends in bridge design, construction, and maintenance. Thomas Telford, London, 45–58.
Frangopol D. M., Kong J. S., Gharaibeh E. S. (2001), “RELIABILITY-BASED LIFE-CYCLE MANAGEMENT OF HIGHWAY BRIDGES”. J. COMPUT. CIVIL ENG., 15(1), 27-34.
Frangopol D. M., Kong J. S., Gharaibeh E. S. (2001), “Reliability-based Life-Cycle Management of Highway Bridges”. J. COMPUT. CIVIL ENG., (1), 27-34.
H. N. Li, T. H. Yi, Liang R., D. S. Li and L. S. Huo (2014), “Reviews on innovations and applications in structural health monitoring for infrastructures”. Struct. Monit. and Maint., 001-045.
Helder S., João B., Joaquim F. (2013), “Construction assessment and long-term prediction of prestressed concrete bridges based on monitoring data”. ENG. STRUCT., 52, 26–37.Ko J. M., Ni Y. Q. (2005), “Technology developments in structural health monitoring of large-scale bridges”. ENG. STRUCT., 27, 1715-1725.
Liu Y. F., Lu D. G., Fan X. P. (2014), “Reliability updating and prediction of bridge structures based on proof loads and monitored data”. CONSTR. BUILD. MATER., 66(15), 795–804.
Muria V. D., Comez R., King C. (1991), “dynamic structural properties of cable stayed tampico bridge”. J. Struct. Eng., 11 (117).
Mufti A. A. (2002), “Structural health monitoring of innovative Canadian civil engineering structures”. STRUCT. HEALTH. MONIT., 1 (1), 89-103.
Mustafa G., F. N. Catbas. (2009), “Statistical pattern recognition for Structural Health Monitoring using time series modeling: Theory and experimental verifications”. MECH. SYST. SIGNAL PR., 23 (7), 2192–2204.
Niu D. T., Wang Q. L. (1995), “Models of concrete strength changing with time in general air environment”. Ind. Buildings, (6), 36~38.NIuadi D. A. (2002), “Monitoring of a concrete arch bridge during construction”. SMART MATER. STRUCT. , 4696-5017.
Simon D. N., Merit E., Jacob E. A., et al. (2011), “Messina Bridge-Structural Health Monitoring System”.
Stewart M. G., Mullard J. A. (2007), “Spatial Time-Dependent Reliability Analysis of Corrosion Damage and the Timing of First Repair for RC Structures”. Eng. Struct., (29), 1457-1464.Sunyong K., D. M. Frangopol. (2010), “Optimal planning of structural performance monitoring based on reliability importance assessment”. PROBABILIST ENG. MECH., 25 (1), 86-98.
T.H.T. Chan, L. Yu, H.Y. Tam, Y.Q. Ni et al. (2006), “Fiber Bragg grating sensors for structural health monitoring of Tsing Ma bridge: Background and experimental observation”. Eng. Struct., 28 (5) , 648–659.
Thoft-Christensen P. (1995), “Advanced bridge management systems”. Struct. Engrg. Rev. Oxford, England, 7(3), 151–163.Thoft-Christensen P. (1999), “Estimation of bridge reliability distributions”. Current and future trends in bridge design, construction, and maintenance. Thomas Telford, London, 15–25.
The transportation department specification of the people’s Republic of china (2004), “Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG D62-2004)”. China Communications Press, Beijing.
Wong K. Y. (2004), “Instrumentation and health monitoring of cable-supported bridges”. STRUCT. CONTROL HLTH., 11 (2), 91–124.
Zhang J. L., Liu Y (2004), “Statistical Models for the Lifetime Resistance of Concrete Bridges”. Journal of Changsha University of Science, 1(1), 27~33.
Zhang W., Shi B., Zhang Y. F. (2007), “The strain field method for structural damage identification using Brillouin optical fiber sensing”. Smart Mater. Struct, 16, 843-850.




