轿车悬架控制臂参数化建模及轻量化多目标优化设计
本文摘要(由AI生成):
本文研究了某轿车前悬架控制臂的轻量化设计。通过提取四种工况下的受力,建立了控制臂的有限元和拓扑优化模型,并利用NSGA-II算法进行了多目标优化设计。结果显示,轻量化后的控制臂在保持性能基本不变的情况下,质量减轻了15.6%,低频固有振动特性得到较大改善,强度和刚度满足设计要求。该研究为汽车悬架控制臂的轻量化设计提供了有效方法。
王登峰 1 黄亚威 1 秦民 2 蒋永峰 2
(1.吉林大学 汽车仿真与控制国家重点实验室;2.中国第一汽车股份有限公司技术中心)
【摘要】提取了汽车在加速、制动、稳态回转和最高车速行驶4种工况下前悬架控制臂的载荷,建立了控制臂的拓扑优化分析模型。以控制臂质量最轻、最大变形最小为目标函数,以控制臂的1阶弹性模态频率不低于轻量化前的频率及控制臂最大米塞斯应力小于材料的许用应力为约束条件,以控制臂参数化模型的 11 个参数为设计变量,建立了控制臂 轻量化多目标优化设计数学模型。用第二代非劣排序遗传算法(NSGA-II)对控制臂进行轻量化多目标优化设计结果表 明,在保持控制臂低阶固有振动特性、强度和刚度基本不变的条件下,轻量化后控制臂质量从 2.62kg 减少到 2.21kg,减重 15.6 %,轻量化效果明显。
1 前言
目前,国内、外汽车企业和研发机构对控制臂的轻 量化优化设计进行了一些研究工作。文献[1]和文献 [2]运用拓扑优化和形状优化方法对控制臂进行了优 化,减轻了控制臂质量。文献[3]~文献[5]首先对悬架 控制臂进行了简单的性能分析,然后对控制臂进行了 单目标优化,既实现了减重目标,又满足了控制臂的性能要求。文献[6]将可靠性理论引入轻量化设计中,在 不同工况下对悬架控制臂进行了轻量化设计,取得了 较好的减重效果。
本文针对某轿车前悬架下控制臂质量偏重问题, 对其进行参数化建模和轻量化多目标协同优化设计, 在满足控制臂主要性能要求的前提下有效减轻了其结构质量。
2 控制臂载荷提取
利用所建立的考虑前悬架控制臂弹性的整车刚弹 耦合虚拟样机模型[7],按照国家标准 GB/T 12543-2009《汽车加速性能试验方法》、GB 12676-1999《汽车制动 系统结构、性能和试验方法》、GB/T 6323.6-1994《汽车 操 纵 稳 定 性 试 验 方 法 —— 稳 态 回 转 试 验》和 GB/T 12544-2012《汽车最高车速试验方法》规定的要求,在所 建B级路面上分别进行整车加速、制动、稳态回转和最高 车速直线行驶仿真分析,在整车坐标系下提取前悬架下控 制臂与车身连接前、后点及转向节连接外点处不同工况 下所受 X、Y 和 Z 方向载荷时间历程,经数据处理和分析, 求取各个力的均值和标准差,按均值加上 3 倍标准差的3σ 原则,确定出前悬架下控制臂所受载荷如表1所示。
表 1 不同工况下前悬架控制臂承受的载荷 N
位置 | 方向 | 加速工况 | 制动工况 | 最高车速工况 | 稳态回转工况 |
外点 | FX | 5460.0 | 1370.6 | 2180.6 | 1170.4 |
FY | 3730.6 | 895.0 | 988.8 | 1685.0 | |
FZ | 118.0 | 107.6 | 64.8 | 117.0 | |
前点 | FX | 432.8 | 710.5 | 173.0 | 268.4 |
FY | 9979.5 | 2272.3 | 2497.8 | 2033.1 | |
FZ | 2454.8 | 614.3 | 1103.0 | 631.5 | |
后点 | FX | 326.0 | 349.3 | 63.7 | 39.4 |
FY | 2812.3 | 2260.7 | 1131.2 | 542.3 | |
FZ | 1282.6 | 1026.5 | 592.2 | 375.3 |
3 控制臂拓扑优化与参数化建模分析
3.1 控制臂有限元建模
为了获取前悬架下控制臂的最优结构拓扑,需要建 立控制臂的有限元模型和拓扑优化模型。控制臂有限 元建模时采用板单元对其进行离散化,共划分为 10507 个节点、10150 个四边形单元、153 个三角形单元和 3 个 REB2 刚性单元,经网格质量检查,所建有限元模型满足 计算分析要求,如图 1 所示。
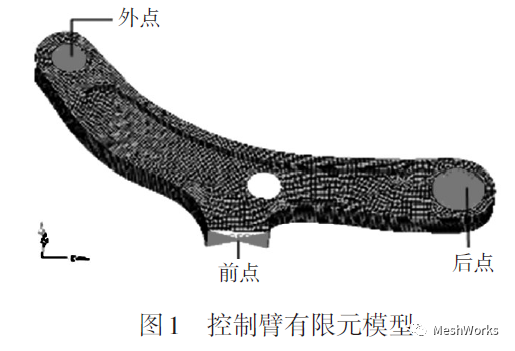
3.2 控制臂拓扑优化建模与分析
在建立控制臂拓扑优化模型时选用变密度法,以材 料密度作为拓扑优化设计变量,定义1个质量响应和4种不同工况下的节点位移响应,以除去控制臂外点和后点安装孔以外的其它全部模型区域为设计区域,以表 1 中载荷作用下控制臂节点最大位移作为约束,以控制臂 质量最轻作为目标函数,得到控制臂拓扑优化模型如图 2 所示。

图 2 控制臂拓扑优化模型
在 Hyperworks/Optistruct 模块中进行控制臂的拓扑优化计算,得到优化后控制臂的相对密度云图如图3所示。综合考虑控制臂的冲压加工工艺、结构性能和减重要求,从中提取控制臂的拓扑结构如图 4 所示。
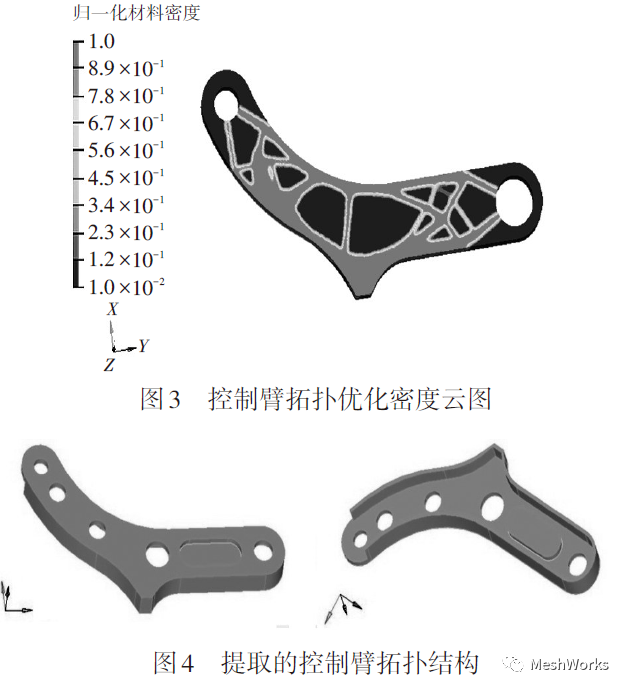
3.3 控制臂参数化建模
用美国的 DEP MeshWorks/Morpher 参数化设计软件,进行控制臂的参数化建模,共定义12个参数来描述控制臂结构,如图5和表2所示。表2中的 DV12 为有限元网格质量参数,即考虑到优化后控制臂有限元网格会发生变化,网格质量也会随之发生变化,为避免因网格质量畸变导致模型无法计算,需要专门定义一个宏参数 DV12 来保证网格质量。
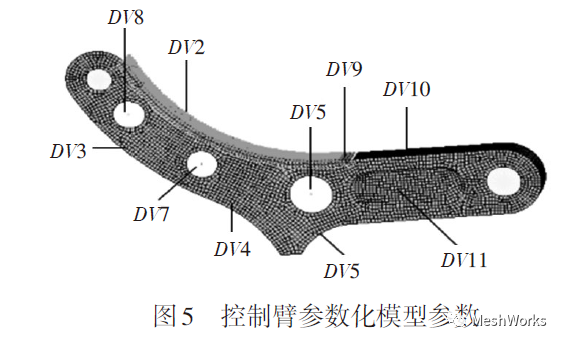
表2 控制臂参数化模型中各参数及变化范围
参数 | 参数描述 | 参数变化范围/mm |
DV1 | 控制臂板厚 | 2.0~6.0 |
DV2 | 圆弧半径与原半径之比 | 0.975~1.025 |
DV3 | 圆弧半径与原半径之比 | 0.975~1.025 |
DV4 | 圆弧半径与原半径之比 | 0.975~1.025 |
DV5 | 圆弧半径与原半径之比 | 0.95~1.05 |
DV6 | 圆孔半径与原半径之比 | 0.25~1.25 |
DV7 | 圆孔半径与原半径之比 | 0.25~1.25 |
DV8 | 圆孔半径与原半径之比 | 0.25~1.25 |
DV9 | 翻边高度 | -15.0~15.0 |
DV10 | 非圆弧宽度 | -5.0~5.0 |
DV11 | 槽深度 | -5.0~0.0 |
DV12 | 网格质量参数 | — |
4 控制臂轻量化多目标优化设计
4.1 多目标优化模型
在建立控制臂轻量化多目标优化设计模型时,以表2中前11个参数作为优化的设计变量 ,以表2中参数的变化范围 、控制臂的1阶弹性模 态频率不低于轻量化前的频率190 Hz 及控制臂最大应力小于QSTE420TM材料(屈服强度为 420 MPa)的许用应力280 MPa(取安全系数为 1.5)为 优 化设计的约束条件,以控制臂质量最轻、最大变形最小为目标函数,得到控制臂轻量化多目标优化设计数学模型如下:

4.2 控制臂轻量化多目标优化
用第二代非劣排序遗传算法(NSGA-II)对控制臂 进行轻量化多目标优化设计,经历 100 次迭代后优化过 程终止,共得到9个设计方案。其中,控制臂质量 y1(X)的迭代过程如图 6 所示,圆点表示迭代过程中的非可行方案,9个可行方案在迭代过程中用 x 和*表示,其中*代 表控制臂质量的最优解。通过对最优解进行工程化处理,确定出控制臂的轻量化优化设计方案(表 3)。
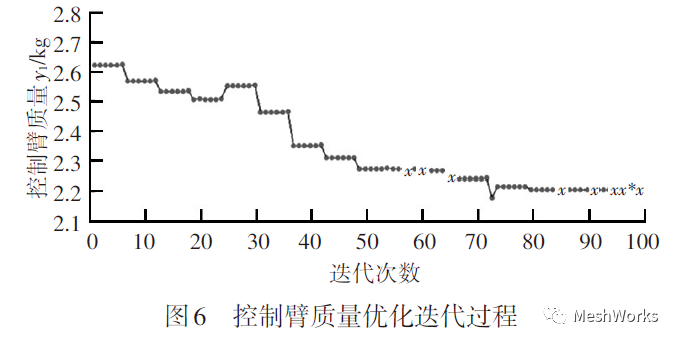
表 3 控制臂参数初始方案与优化方案对比 mm
设计变量 | 设计变量描述 | 初始方案 | 最优解 | 优化方案 |
X1 | 控制臂板厚 | 4 | 3.526 | 3.5 |
X2 | 圆弧半径与原半径之比 | 1 | 0.9961 | 1 |
X3 | 圆弧半径与原半径之比 | 1 | 1.0002 | 1 |
X4 | 圆弧半径与原半径之比 | 1 | 1.012 | 1 |
X5 | 圆弧半径与原半径之比 | 1 | 1.0645 | 1.1 |
X6 | 圆孔半径与原半径之比 | 1 | 1.137 | 1.2 |
X7 | 圆孔半径与原半径之比 | 1 | 0.8960 | 0.9 |
X8 | 圆孔半径与原半径之比 | 1 | 0.7370 | 0.8 |
X9 | 翻边高度 | 0 | -2.148 | -2.1 |
X10 | 非圆弧宽度 | 0 | 0.0015 | 0 |
X11 | 槽深度 | 0 | -0.026 | -0.1 |
将表3中的优化方案带入控制臂的参数化模型,得到轻量化后控制臂质量为 2.21 kg,与原控制臂质量2.62 kg 相比降低 0.41 kg,减重 15.6 %。
5 轻量化控制臂性能分析与对比
5.1 低频固有振动特性对比
为了检验轻量化前、后控制臂的低频固有振动特性,对轻量化后控制臂进行了自由状态下的模态分析, 并与轻量化控制臂在厚海绵上进行的试验模态分析结果进行比较,如表4、图9 和图10 所示。
表 4 轻量化前、后控制臂低频固有振动特性对比
模态 阶数 | 优化后固 有频率/Hz | 优化前固 有频率/Hz | 试验频率/Hz | 优化前与试验结果间相对误差/% | 优化前后 变化量/Hz |
1 | 203.6 | 189.6 | 198.7 | 4.6 | +14.0 |
2 | 223.1 | 240.3 | 226.5 | 6.1 | -17.2 |
3 | 538.4 | 415.6 | 389.6 | 6.7 | +122.8 |
4 | 805.9 | 600.5 | 589.1 | 1.9 | +205.4 |
5 | 946.2 | 776.9 | 767.6 | 1.2 | +169.3 |
6 | 999.5 | 796.6 | 804.2 | 0.9 | +202.9 |
7 | 1302.8 | 835.6 | 819.3 | 2.0 | +467.2 |
8 | 1329.5 | 865.0 | 868.7 | 0.4 | +464.5 |
9 | 1461.7 | 994.5 | 961.9 | 3.4 | +467.2 |
10 | 1538.0 | 1120.5 | 1102.3 | 1.7 | +417.5 |
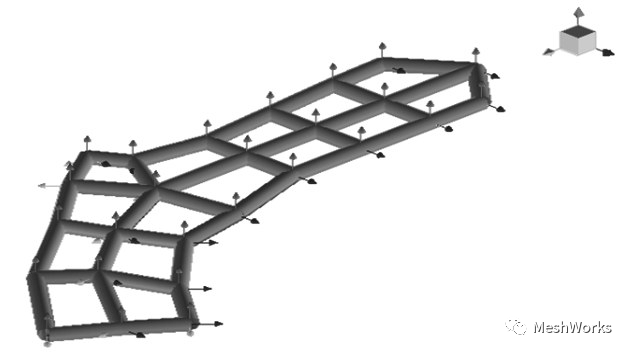
图 9 控制臂试验模态分析测点分布

从表4和图10中可以看出,轻量化前控制臂的前10 阶弹性模态频率有限元分析结果与试验结果的最大相对误差小于7%,从而验证了控制臂有限元模型的正确性;轻量化后控制臂的前10阶弹性模态频率中除了第2阶频率略有降低外,其它9阶频率均有不同程度提高,其第1阶弹性模态频率增加幅度最小,提高14Hz,可见控制臂轻量化后的低频固有振动特性有较大程度改善。
5.2 强度和刚度对比
对轻量化前、后控制臂在加速、制动、稳态回转和最 高车速直线行驶 4 种工况下的最大应力和最大变形进行对比,如表5所示。
表 5 控制臂轻量化前、后不同工况下最大应力和变形对比
工况 | 最大应力/MPa | 最大变形/mm | ||||
原结构 | 轻量化 结构 | 差值 | 原结构 | 轻量化 结构 | 差值 | |
加速 | 275.5 | 267.3 | -8.2 | 1.94 | 1.98 | +0.04 |
制动 | 205.7 | 185.1 | -20.6 | 0.84 | 0.84 | +0.00 |
稳态回转 | 58.5 | 57.4 | -1.1 | 0.10 | 0.11 | +0.01 |
最高车速 | 97.6 | 95.4 | -2.2 | 0.21 | 0.20 | -0.01 |
从表5中可见,控制臂轻量化后在加速、制动、稳态回转和最高车速直线行驶4种工况下的最大应力均略有下降,都小于材料的许用应力 280 MPa;前3种工况下最大变 形稍有增加,第4种工况略有降低,但均变化很小,可见轻量化后控制臂的强度、刚度变化很小,满足设计要求。
6 结束语
a. 提取了某轿车前悬架控制臂在加速、制动、稳态 回转和最高车速直线行驶 4 种工况下的受力,按均值加上 3倍标准差的3 σ 原则,确定出前悬架下控制臂所受载荷。
b. 建立了控制臂的有限元和拓扑优化模型,根据 控制臂的拓扑优化分析结果确定出其最优拓扑结构,并 利用 Meshworks/Morpher 软件进一步建立了控制臂的参数化模型。
c. 建立了控制臂的轻量化多目标优化设计数学模型,用第二代非劣排序遗传算法(NSGA-II)对控制臂 进行轻量化多目标优化设计,确定出了控制臂的轻量化 优化设计方案。
d. 对轻量化前、后控制臂的低阶固有振动特性、 强度和刚度进行分析和对比结果表明,在保持控制臂上 述性能基本不变的条件下,轻量化后控制臂的质量从 2.62 kg 减少到 2.21 kg,减重 15.6 %,轻量化效果明显。
参 考 文 献
Murali M. R. Krishna and ScottV. Anderson. Shape Optimi⁃ zation Application in Upper Control Arm Design. SAE Pa⁃ per No. 2000-01-3445.
Murali M.R. Krishna, Aaron Stange. Topology and Classical Shape Optimization of a Lower Control Arm— a Case Study. ASME 2006 International Design Engineering Technical Conferences &Computers and Information in Engineering Conference. September 10~13, 2006.
3 乐天聪.某轿车悬架控制臂有限元分析与结构优化:[学位 论文].长春:吉林大学,2009.
4 吕宝刚.越野车独立悬架关键零部件的轻量化设计:[学位 论文].长春:吉林大学,2007.
5 秦东杰.某越野车单纵臂拓扑优化设计:[学位论文].长春:吉林大学,2007.
6 扶原放,金达锋.多工况悬架下摆臂结构优化设计方法研 究.机械设计与制造,2009,8.
7 Shi Tianze, Wang Dengfeng,Zhang Youkun and Dong Hon⁃ gliang. Rigid-elastic Coupling Multi-body Dynamics Model⁃ ing for a car and Analysis Optimization of Understeer. Ap⁃plied Mechanics and Materials, 2014, Vols. 490~491:858~862.




