汽车制动系统复模态分析
本文摘要(由AI生成):
本文介绍了制动系统振动特性对整车NVH性能的影响,特别是制动噪声对乘员驾驶感受的影响。文章通过复特征值分析预测制动尖叫倾向性,并基于Hm工具进行制动系统复特征值分析。文章详细阐述了复特征值理论、制动系统数学模型及振动方程,并通过案例实战展示了如何建立制动系统模型、设置载荷和求解复特征值。最后,文章总结了制动系统制动噪声问题的复杂性及优化调整的重要性,并提供了负阻尼比的阈值参考。
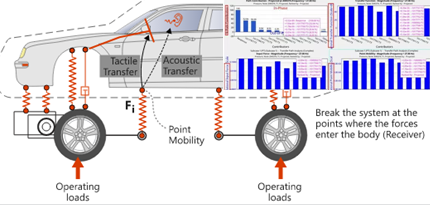
制动系统是汽车中一个非常重要的系统,其制动系统的振动特性影响着整车NVH性能,特别是制动噪声直接影响乘员的驾驶感受。当前对制动系统进行噪声尖叫分析,可以由试验进行,或通过仿真方法,如采用Abaqus或Hm进行复特征值分析,通过复特征值分析可以预测摩擦产生的制动尖叫倾向性。一般复特征值的虚部表示振动频率,实部表示振动阻尼,当实部为正值时,表明系统不稳定,有产生摩擦尖叫的倾向。本期我们基于Hm工具进行某制动系统复特征值分析。
一、相关理论
制动系统的复特征值理论建立制动系统的数学模型进行振动分析,有助于我们更深刻更直观地了解噪声机理。有阻尼制动系统的自由振动方程为:
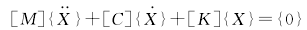
其中:[M]、[C]、[K]分别为系统的质量矩阵、阻尼矩阵、刚度矩阵;{X}为振动位移。汽车制动时,制动力垂直作用于制动块,使制动块与制动盘间产生摩擦阻力,达到减速制动系统引入摩擦力时的振动方程为:
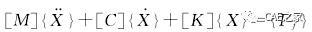
其中:{Ff}为摩擦力,{Ff}=[Kf]{X},通过转换可得

摩擦力导致的系统刚度耦合,系统刚度矩阵不对称,特征矩阵不对称,求解出的特征值有些是复数,即系统各阶模态频率和模态振型都是复数,即系统各阶模态频率和模态振型都是复数如下式:

其中 为特征向量;s为特征值。通过转换可得以下公式:
为特征向量;s为特征值。通过转换可得以下公式:

能上式求解可得特征值和特征向量。系统第i阶特征值为:
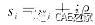
其中:αi为实部,即为系统的不稳定系数;βi为虚部,即为系统的不稳定频率。

二、案例实战
1、模型说明: 如通过建立有限元模型,某制动系统模型如图1所示,简易模型包括制动盘、摩擦片及固定支架等。

图1 简易制动系统模型
2、载荷说明: 如该制动系统包括三个子工况,分别是(1)制动过程制动力作用于制动盘工况,(2)制动盘旋转工况,(3)复特征值计算工况。
(1)工况一及二定义:制动压力为2.0MPa,以及2Km/h的制动速度。各零件之间需要建立接触,摩擦系统如设为0.3,采用面面接触,该工况为非线性准静态工况。

图2 接触设置

图3 工况1边界设置
(2)工况三定义:复特征值计算,具体方法见公 众号文章《流固耦合模态分析探讨》,包括Eigrl和EIGC设置。

图4 正则模态设置

图5 复特征值模态设置
(3)全局参数设置。制动系统属于接触非线性问题,需要设置接触相关参数,如NLPARM,CONTF,EXPERTNL等。
3、求解计算: 通过读取out文件,可以得到所需要的信息,如复模态频率的虚部和代表模态阻尼的实部。如果实部是负的,则系统是稳定的。如果实部是正的,则系统是不稳定的。复模态实部大于0,则表明模态阻尼比为负数,在振动过程中振幅会随时间的增加越来越大,因此该阶模态下系统不稳定。复模态的特征值如下所示:

图6 复模态特征值结果
三、小结
(1)制动系统制动噪声是高频噪声问题,在实际工程中此类问题遇到很多,制动尖叫问题属于复特征值问题,可通过试验或仿真得到相关频率或阻尼特性,进而进行优化调整;
(2)根据工程实践,在不考虑材料阻尼的情况下,国内一般将负阻尼比小于-0.01设为引发噪声模态的阈值,而较严格的企业通常选用-0.006作为阈值;
(3)制动系统制动尖叫属于高度非线性问题,涉及到材料非线性,边界非线性以及 摩擦噪声自激励等相关内容,需要进行大量的仿真和试验积累。
【免责声明】本文首发CAE之家公 众号,欢迎关注我的公 众号“CAE之家”。未经授权禁止私自转载,本公 众号所刊登的内容、资料等来自于个人总结、技术论坛、文献、软件帮助文档及网络等,对文中观点判断均保持中立,若您认为文中来源标注与事实不符,若有涉及版权等请告知,将及时修订删除,谢谢大家的关注!