01
问题的提出
01
问题的提出
为了适应现代战争的需要,战术导弹已逐渐采用大攻角控制方式, 而且已在很多新型导弹上使用, 例如垂直发射的地空导弹、舰空导弹、采用BTT (Bank-To-Turn) 技术的战术导弹。无论是垂直发射的战术导弹,还是BTT导弹,为了使导引头能够捕获目标,均要求精确地控制导弹的姿态,这就要求实时地测量弹体的姿态。通常,采用机械平台或捷联系统来测量弹体的姿态。在导弹大机动情况下,用传统的框架式自由陀螺仪测量弹体姿态, 将会出现陀螺倾翻。国外有人在此基础上通过增加框架来解决此问题, 获得成功,但是结构复杂、成本昂贵, 所以, 对于战术导弹来讲实用价值不大。而捷联系统是一个无框架系统,一般由三个速率陀螺、三个加速度陀螺和一台微机组成,通过计算机建立一个数学的稳定平台,通过方向余弦进行坐标转换。由此可见捷联系统具有体积小,质量轻、成本低和可靠性高等优点,所以,在战术导弹系统中被逐渐广泛采用。
通常,在导弹姿态控制系统中,弹体的三个姿态角(俯仰角θ、偏航角Ψ、滚转角γ)要直接用来参加控制。可是,当导弹俯仰角趋近于90°时, 姿态角表示法存在奇异性问题, 即姿态角Ψ, γ具有多值性。
另外, 在捷联系统中速率陀螺测量沿弹体三个轴的角速度ωx,,ωy, ωz,计算机根据角速度计算弹体姿态, 姿态解算主要由以下几步完成:

其中(1-3)式是根据偏航角Ψ、俯仰角θ、滚转角γ的姿态角顺序得出的。由(1-3) 式可知θ角可由T21得出Ψ角可由T11和T31消去cosθ得出。γ角可由T22, T23消去cosθ得出。可见解算姿态角的计算量较大, 所以将对捷联计算机提出较高的要求。
鉴于上述情况, 我们考虑采用四元数来表示弹体姿态,并进行姿态控制系统设计,这样既可解决姿态角表示法存在的奇异性问题,又可减少捷联系统的计算量, 从而降低对计算机系统的要求,这一点对战术导弹来讲具有重要实用价值。
本文首先给出了大机动飞行情况下弹体的动力学模型。然后, 基于非线性系统解耦控制思想设计了姿态控制系统,并验证了系统的稳定性。最后, 通过数值仿真验证了本文提出方法的有效性。
02
弹体动力学模型
考虑到导弹姿态控制的特点以及敏感元件均安装在弹体坐标系上,我们采用弹体坐标系来描述导弹的运动, 从而可写出弹体的三个转动方程:
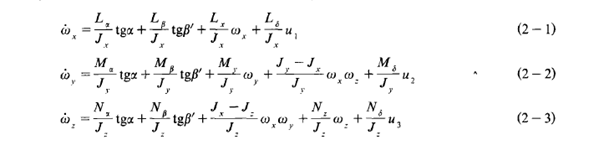
其中α为攻角, β′为反映了侧滑角β大小的一个物理量,当β较小时, β′近似等于β,Jx,Jy,Jz,Lx,Lα,Lβ,Lδ,Mα,Mβ,My,Mδ,Nα,Nβ,Nz,Nδ是适当常数。
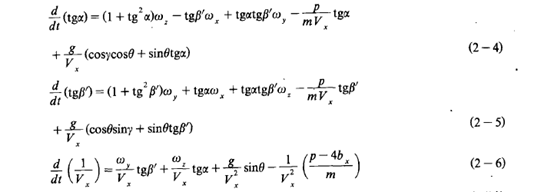
其中g是重力加速度,p为发动机推力, m 为导弹质量,Vx为导弹飞行速度V 在弹体轴x 上的分量,bx为适当常数。
我们引入状态变量tgα tgβ′,采用文献[3]的处理方法, 可得比较( 1-2) 、(l-3)式可知,
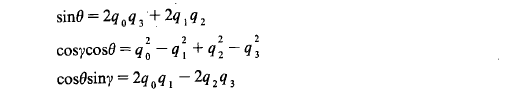
将上述各式代入(2-4) 、(2-5) 、(2-6) 式, 并定义状态变量

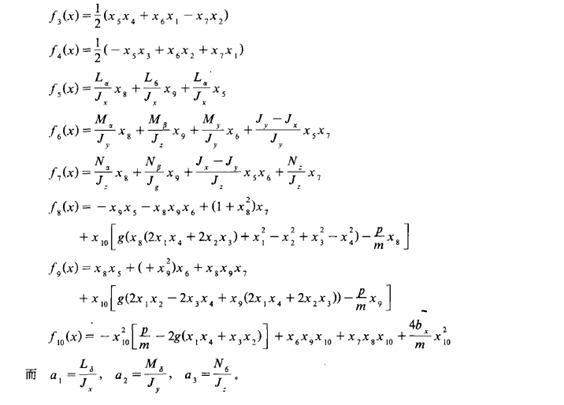
03
姿态控制系统的设置
对于(2-8) 式描述的弹体姿态动力学模型,为了实现解耦控制,我们选择四元数分量q1,q2,q3作为系统(2-8) 的输出量,即
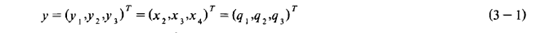
并采用非线性输出解耦方法进行姿态控制系统设计。
为了叙述问题方便, 引入下列算子A
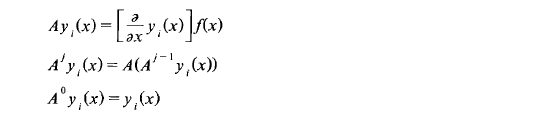
这样,根据(2-8) 、(3-l)式可得
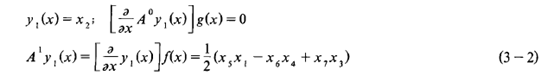

成立, 那么此时x2=q1=1,再根据(l-2)、(1-3)式计算可知此时θ=0,Ψ=0,γ=180°。而对于我们所考虑的问题γ不可能达到180°, 所以(3-7) 式不可能成立, 从而也说明
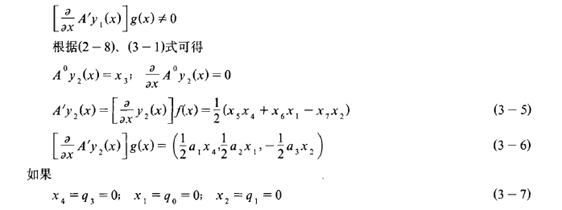
成立, 那么此时x3=q2=1,再根据(l-2)、(1-3)式计算可知此时θ=0,Ψ=180°,γ=0。而对于我们所考虑的问题Ψ不可能达到180°, 所以(3-7) 式不可能成立, 从而也说明

成立, 那么此时x4=q3=1。再根据(l-2)、(1-3)式计算可知此时θ=0,Ψ=180°,γ=180°,而对于我们所处理的问题,Ψ,γ不可能达到180°, 所以(3-10) 式不可能成立, 从而也说明

我们定义

由于本文所讨论的导弹在大机动飞行情况下, 状态变量x1(q0) 始终保持大于零, 所以可判定系统(2-8) 在选择( 3-l) 式所示输出变量的情况下满足完全输出解耦控制的充要条件。
根据( 3-2) 式,可得
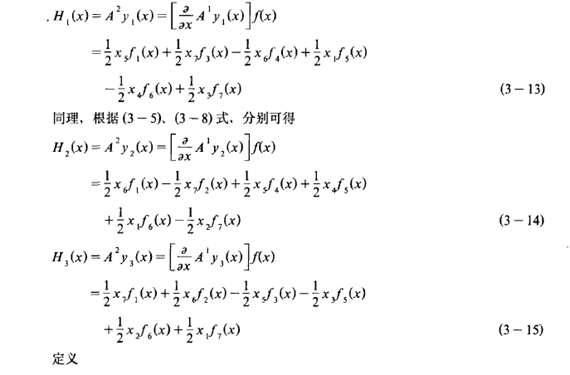

综合上述推导结果,可得系统(2-8)在选择x2,x3,x4 作为输出变量情况下的解耦控制律

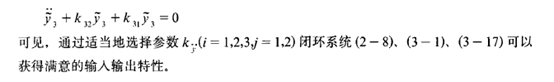
05
仿真验证
我们对(2-8)、( 3-l)、(3-17) 式所示的,由四元数所描述的姿态控制系统进行了数值仿真, 系统参数分别取为

为了讨论问题方便, 我们将解藕输入输出闭环系统(3-18) 写成如下一般形式

其中M,N是确定的正定矩阵,用来产生理想的闭路响应。为使问题简单, 我们选择

其中I是(3×3) 的单位矩阵。(5-l)、(5-2) 式表明对系统状态x2, x3,x4的输出误差产生阻尼比为ζ,频率为ω0的二阶响应。通常, 可以通过增加ζ和ω0来增加系统的稳定性,因为这增加了M,N 的正定性, 如果ζ,ω0的值太小, 系统的不确定性等误差项就会对系统动特性起主导作用, 最终导致不稳定, 本文通过仿真认为取ζ=0.7~1.0,ω0=3~6 rad/s 比较合适。
图1~图4 给出了在如下初始条件下
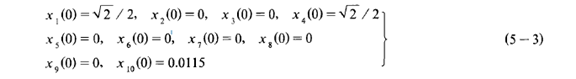
给定参考输出取定为

情况下的四元数分量q0,q1,q2,q3随时间的变化曲线。图5~图7别给出了相应俯仰角θ、偏航角ψ、滚转角γ随时间的变化曲线。
值得指出的是, 初始条件( 5-3) 对应的姿态角是
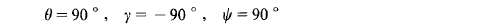
而给定参考输出( 5-4) 式对应的姿态角是
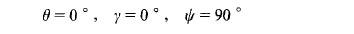
从仿真结果可以看出, 基于四元数推导得到的控制律( 3-17) 实现了弹体姿态的大机动控制,而且控制精度较高,从而也证明了本文提出方法的有效性。
06
结束语
本文提出并研究了基于四元数进行战术导弹姿态控制系统的设计问题。研究结果表明,这一方法是可行的,它不仅解决了姿态角表示法存在的奇异性问题, 而且可减少捷联计算机的计算量, 这一点对战术导弹来讲具有重要实际意义。
本文主要讨论了姿态控制系统的设计问题, 有关这种形式姿态控制系统的实现问题有待进一步研究。另外, 取不同的四元数分量作为直接被控制量(即系统输出量), 将得到不同形式的控制规律, 那么选择哪三个分量作为系统输出为好, 或者采取其它的控制方法等问题也有待进一步研究。
感谢您阅读,我们下期见!
如有内容来源于互联网,版权归原作者所有,供学习交流使用,严禁商用,如有侵权请联系我们删除。
------------------------------------------