基于LES的光滑球体阻力危机模拟
正文共: 865字 10图 预计阅读时间: 3分钟
1 前言
阻力危机指的是流场的雷诺数增加到一定程度时,其阻力系数突然下降的现象。下图为光滑球体的阻力系数和雷诺数的关系曲线,整个曲线可以分为亚临界区(subcritical)、临界区(critical)、超临界区(supercritical)和跨临界区(transcritical)。今天,我们用fluent模拟一下光滑球的阻力危机现象。

2 建模与网格
按如下尺寸建立光滑球外流场计算模型,其中光滑球的直径为Φ42.7mm。划分多面体网格,注意由于本案例需要用到大涡模拟LES,因此边界层网格划分20层,主要控制目标使得99%以上的边界面Y+小于1.0。


2 求解设置
多数前人研究表明,对于该问题的模拟,采用LES大涡模拟可以更为准确的捕捉边界层的分离和再附着现象,但是该模型对计算资源要求很高。本案例采用LES模型。
入口采用速度边界,出口采用压力出口边界。
时间步长1e-5~1e-3之间,来流速度更大时,时间步长要更小,不然连续性方程很难收敛。
设置参考值,用于计算阻力系数,面积为球体垂直投影面积,速度为来流速度。

3 计算结果
来流速度3.42m/s,亦即雷诺数为1e4时,阻力系数的动态曲线如下,最后趋于均值0.46左右。

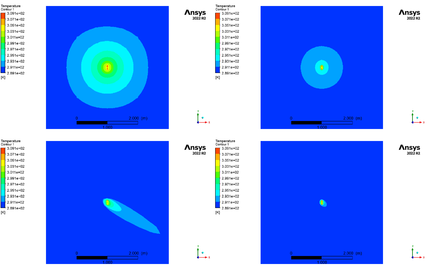
我们看一下此时的涡分布,边界层分离点约在球体中间往前。

来流速度136.87,亦即雷诺数4e5时,阻力系数的动态曲线如下,均值约为0.24,显然,此时已经达到临界区以上了,发生了阻力危机。

我们看一下此时的涡分布,边界层分离点显著延后了,这是造成阻力系数下降的原因所在。

光滑球的阻力系数和雷诺数的关系模拟值如下图,和参考文献[1]的实验曲线较为接近,说明采用LES模拟该问题是可行的。另外,受限于计算资源,跨临界区域的模拟未能开展。


参考文献
[1] Experiments on the flow past spheres at very high Reynolds numbers.
[2] Numerical investigations of flow over a sphere in the subcritical and supercritical regimes