Mathematica 爱心首饰 IV: 爱心树
本文摘要(由AI生成):
本文介绍了使用计算机图形学和3D打印技术创建一颗三维爱心树的过程。通过旋转叶子使其面向边界法向向量,采用正向运动学变换和旋转矩阵调整叶子坐标系的方向。通过增加顶点数量、调整叶子姿态和大小、应用不同关联函数,使树模型更加生动。为了适应3D打印技术,将模型转换为浮雕图,并最终通过MJP工艺和失蜡法铸造制成项链吊坠。整个过程展示了从算法设计到3D打印的完整流程,以及如何通过技术手段模拟和呈现自然界的美丽。

动机
几年前,当我为女儿们朗读《爱心树》的儿童绘本时,我发现原书名"The Giving Tree" 并未被根据字面意思而直译出来,译者调整了词汇并为作者代言,以此表达"爱就是给与"。
树不仅是我们这个星球上一种常见的植物,而且还是"计算元宇宙"中一个重要的概念,它已被广泛应用于艺术、电子游戏和电影产业。本文我将会以最自然地方式来创建一颗自然界并不存在的三维爱心树。此后我将把这颗树设计变换为深度函数并以浮雕图的方式作为一件项链首饰的图案。
下表列出了所有 Wolfram Language 中和 Tree 相关的函数:


边界

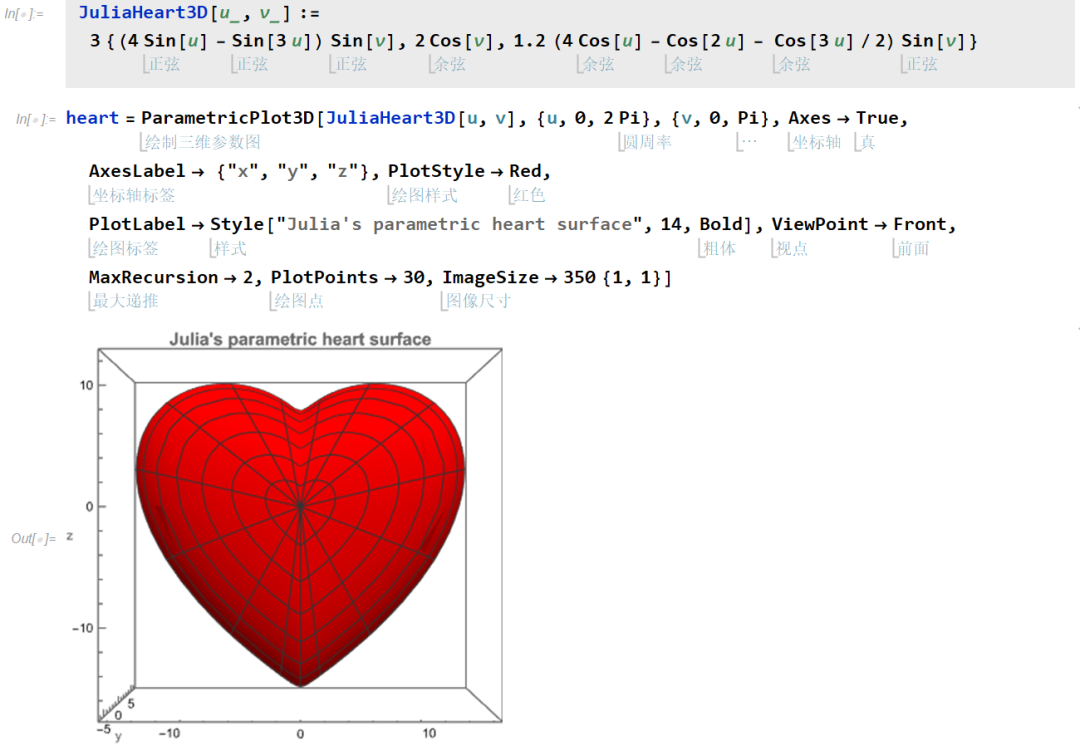
采用 Julia's parametric equation (https://community.wolfram.com/groups/-/m/t/2142619),画个三维爱心模型。
移除一个维度 (y),获得二维平面的 Julia 参数曲线。

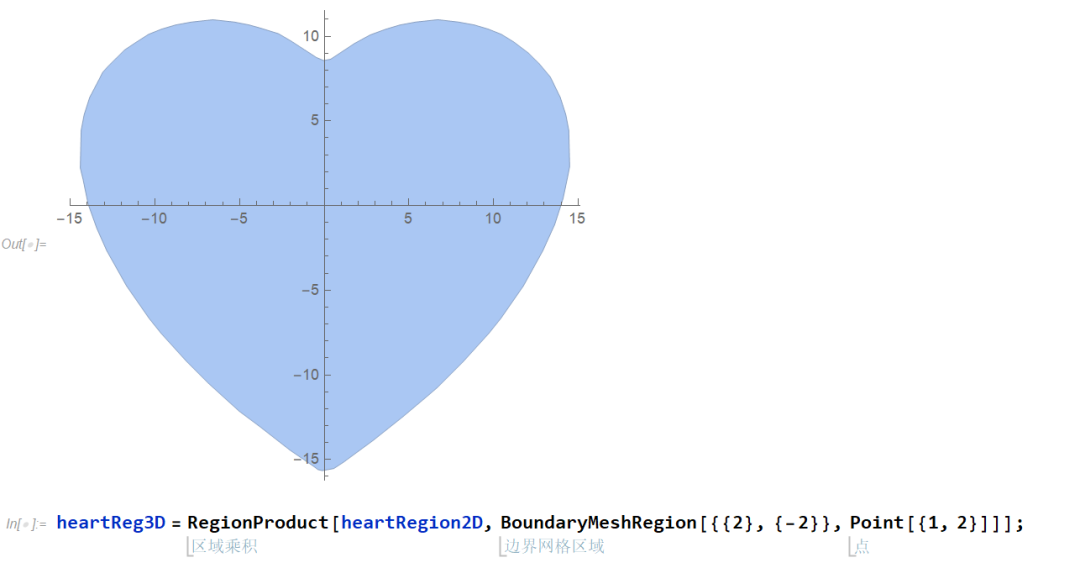
Julia 参数曲线 画二维区域运行有点慢并且边界质量低,于是我重新缩放了尺寸采用第一爱心曲线来创建一个高质量的二维区域。

拉伸平面区域变成三维物体:


树的设计
导入一个小规模的多面体三维爱心区域作为工作区域:

在边界面上生成一些空间均匀分布的随机点,此处我选择小于20个随机点,主要是为了清晰说明和视图简介,数据规模稍后可以变的更大。

最小生成树(https://demonstrations.wolfram.com/GreedyAlgorithmsForAMinimumSpanningTree/),参考文献 [1],它是后面施泰纳最小生成树的基础算法。

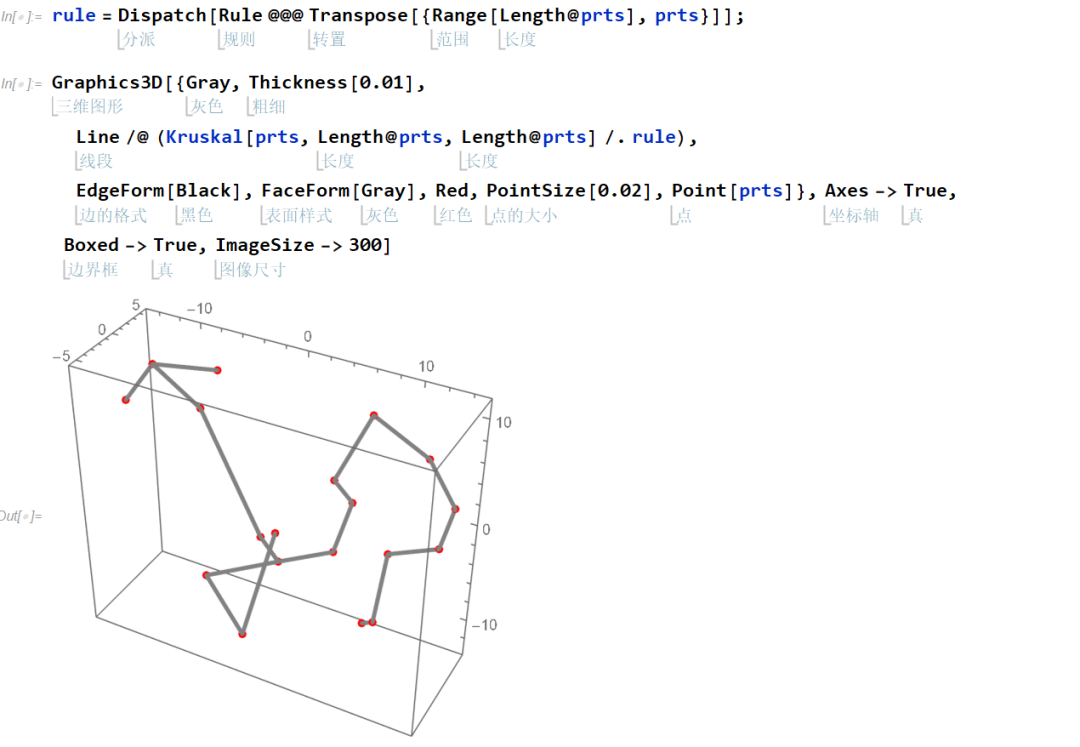
施泰纳最小生成树 Steiner minimal tree,它是一个 NP-complete 问题,所以我采用了一个经典算法,参考文献 [2]:

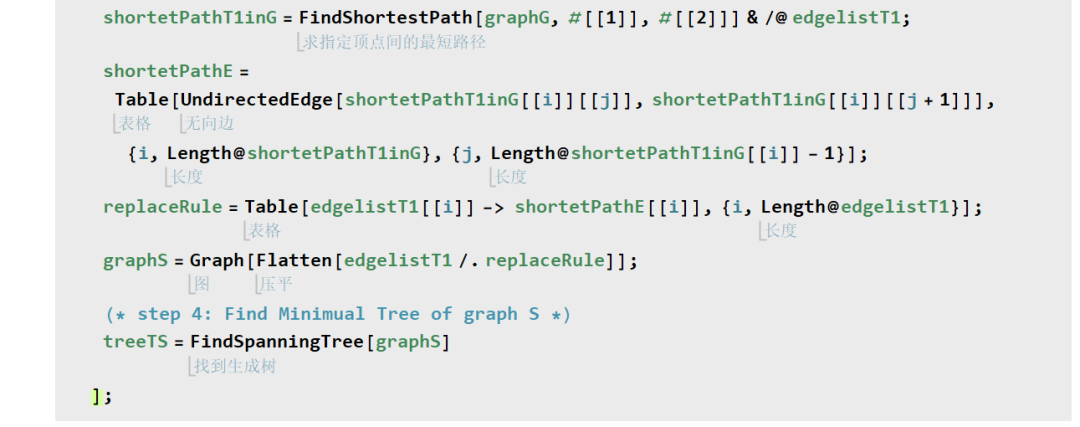
采用施泰纳最小生成树一个优势是,该算法可以自动的生成一些中心区域的补充点,即所谓施泰纳点 Steiner points。

2.4.1 指定树根(位置)

2.4.2 找出树叶(位置)

2.4.3 找出树枝(路径)
找出树枝,路径顺序从树叶到树根。

基于之前抽象的施泰纳最小生成树的图,现在我们生成一颗具体结构的树。我采用 BSplineCurve 和 Tube 来呈现树枝弯曲和直径逐渐变化的生长梯度。


叶的设计
在本章中,树叶是一个宽泛的概念有点像机器人学中的"末端执行器" 。你可以认为它始终是那在树梢末端的一片树叶、一朵花或是一个果实。我的兴趣是展示自然的法则,而不仅仅是复 制自然的形状或结果。叶的姿态和尺寸经过解耦被设计为三个不同目的的函数,并且分别同树枝、重量和阳光(环境)进行关联。本章的核心概念和关联关系如下图所述。
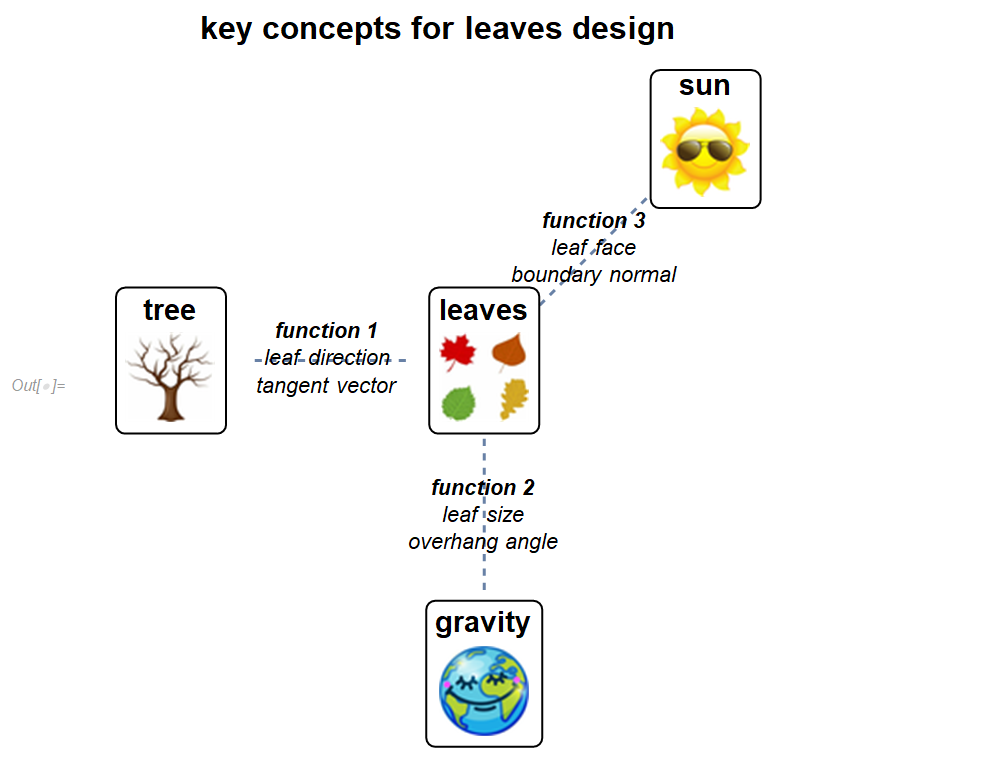
由于叶的位置已经由前面章节中树图中计算而得,下文中我们将具体讨论叶子姿态的最优设计。

创建地表的笛卡尔坐标系 {x0, y0, z0},它是一个固定的绝对坐标系,作为参考坐标系。
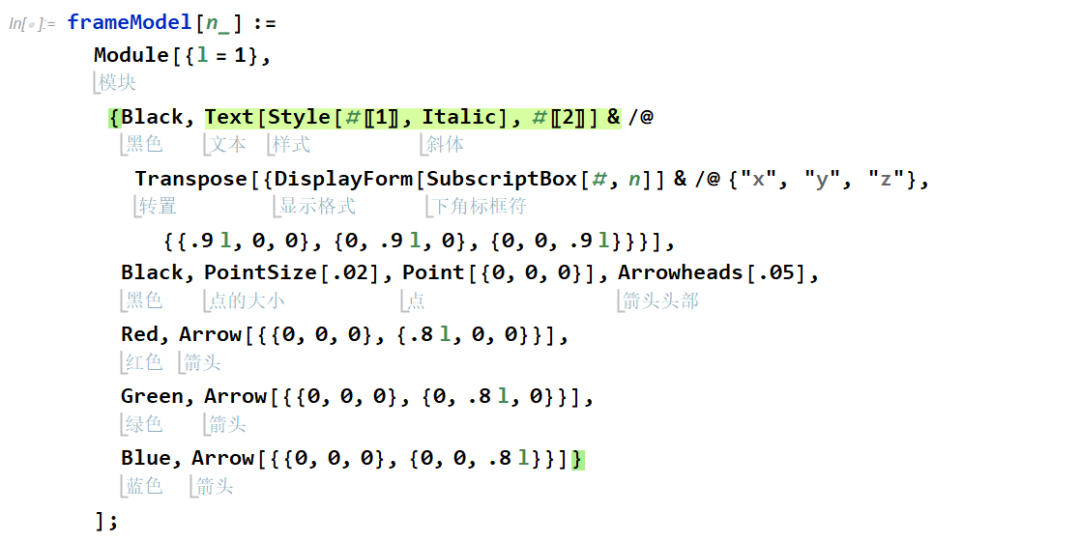
创建单个叶子的笛卡尔坐标系 {x1, y1, z1},它是一个移动的相对坐标系。文中此后叶子坐标系都以三原色 RGB (红绿蓝) 颜色进行标识。
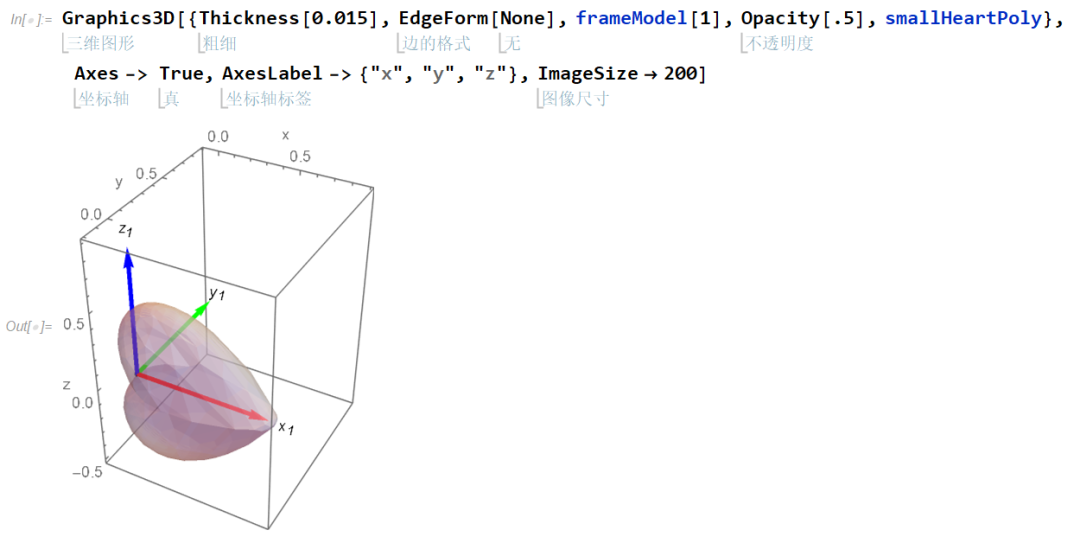
叶子的坐标系可标识并以此控制叶子的姿态,例如当我们将叶子坐标系的 x 方向同树梢末端的切线相重合时,叶子将仅留下一个自由度,即绕该切向量旋转的自由度。
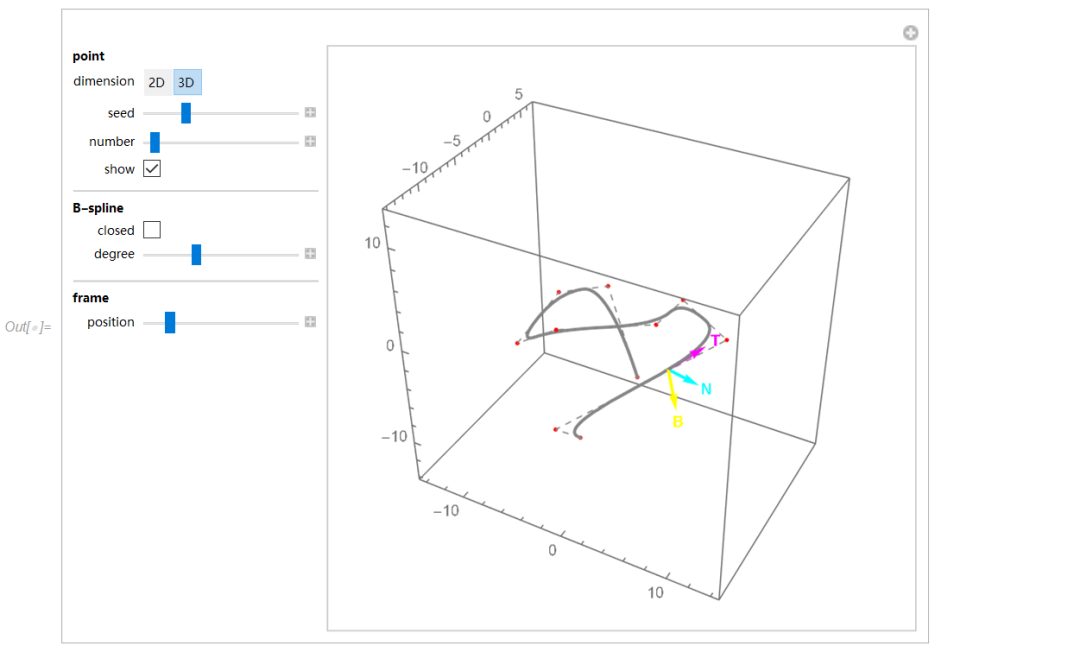
Frenet-Serret移动坐标系(F1+F2+F3)
本小节采用 Frenet-Serret 移动坐标系(切向、法向、副法向)计算了三维树的B样条曲线。Alfred Gray 的书[3]是一本很好的学习曲线和曲面的参考书。

文中此后的 Frenet-Serret 移动坐标系(切向、法向、副法向)都以三原混合色 MCY (品红、青、黄) 标识。
叶子都是从树梢末端生长而出,或者说从树梢末端延伸而出。于是我们基于树枝曲线的切向建立树枝和树叶之间的关系。本小节我将会旋转叶子坐标系并使它同 树枝曲线的 Frenet-Serret 移动坐标系相重合。

如下采用了一个2 自由度耦合的正向运动学变换。
第一个旋转匹配了曲线的切向,更具体得说,使得叶子坐标系的 x 方向同树梢曲线的切向的反方向相重合。这个旋转是本节个的核心内容。
第二个旋转匹配了曲线的法向,更具体得说,使得叶子坐标系的 y 方向同树梢曲线的法向相重合。这个是个暂时的方案,稍后我们还将讨论最好的叶子坐标系的 y 方向。

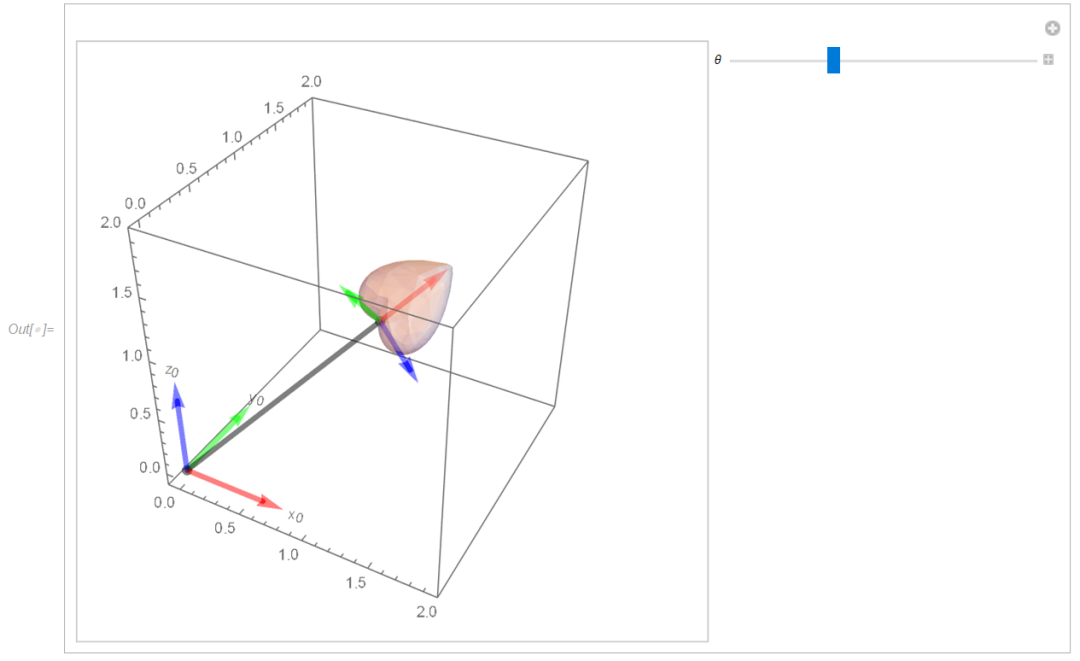
可视化输出带坐标系的树梢和树枝,可见叶子坐标系已同 Frenet-Serret 移动坐标系重合:


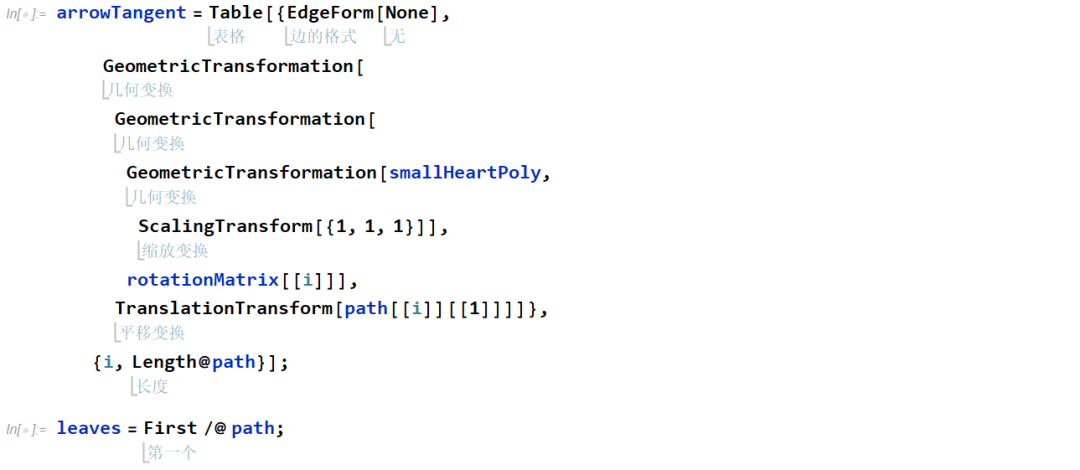
悬挂爱心犹如在一个小树梢上挂个苹果,苹果越重,树梢就垂的越低。此处定义一个"悬垂角",它是从曲线切向到重力垂向的一个矢量角。由于三维地球重力垂向始终是一个固定的向量 { 0, 0, -1} 它位于悬垂线上并指向负方向。

如下视图展示了任意一个向量的悬垂角,该悬垂角同爱心尺寸进行关联。
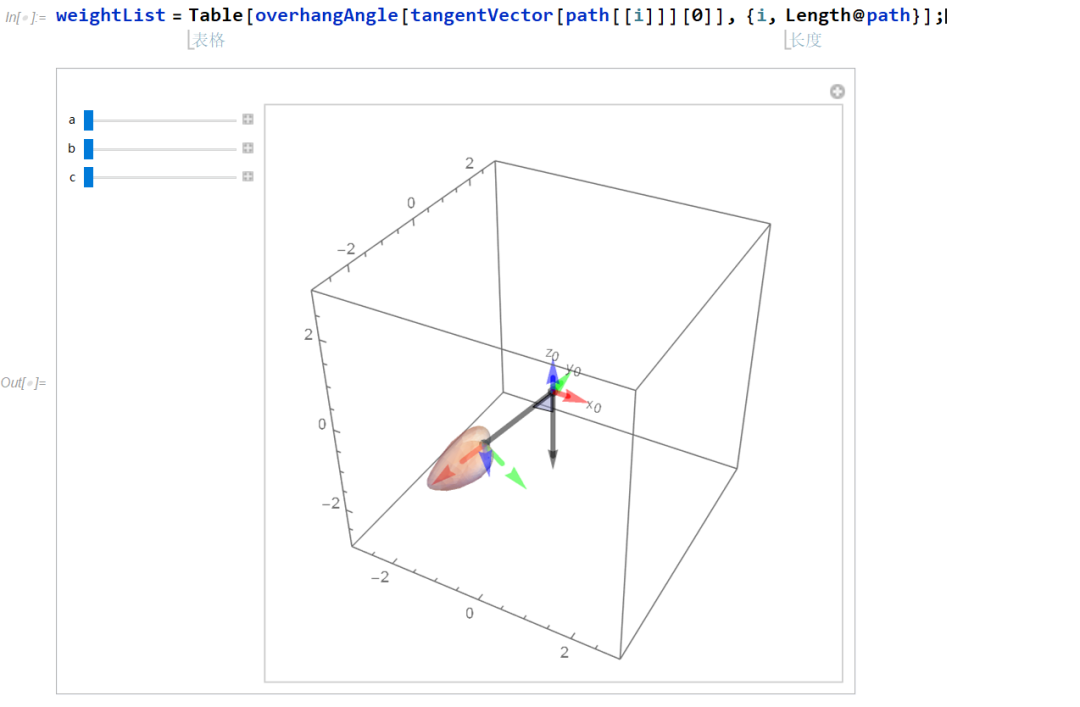
植物的生长始终会朝向光的方向,这一现象称为植物的趋光性。然而自然界中光线或阳光始终是动态的,所谓太阳从东方升起,西方落下。因此大部分情况下,植物的叶子都会位于植物的边界区域上,并且叶子的面会朝外,以此来最大程度的接收阳光。本节预先计算树的边界法向向量,为后文展开做准备。
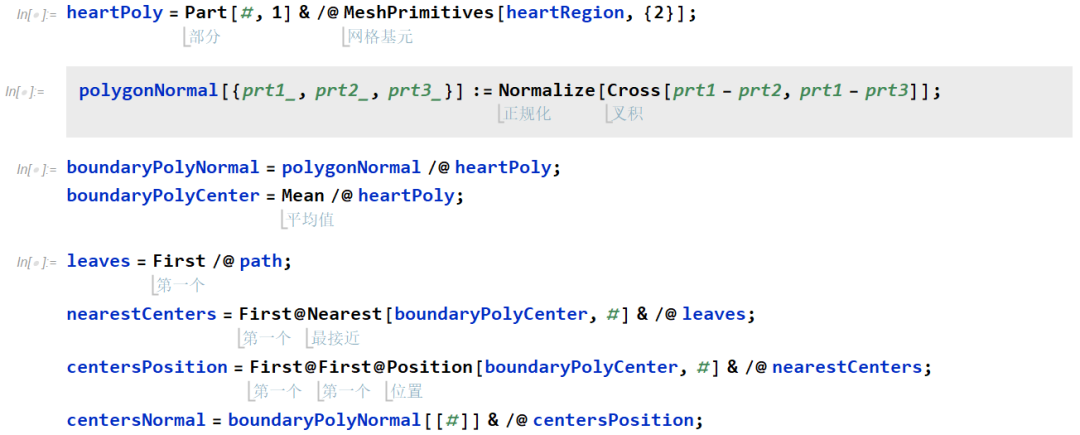
如下图所述,灰色箭头标识边界的的法向向量,橙色箭头代表位于边界上任意一点的法向向量。


本小节我们将旋转叶子使得叶面全部朝向该叶子所在位置的边界法向向量。树边界法向向量将会投影到同切向正交的平面上,以此方向作为旋转方向。

再次使用2自由度耦合的正向运动学变换,第一个旋转使得叶子坐标系的 x 方向同曲线的切向重合,第二个旋转使得叶子坐标系的 y 方向同边界法向向量在正交面的投影方向相重合。

采用旋转矩阵计算所有叶子坐标系的方向:
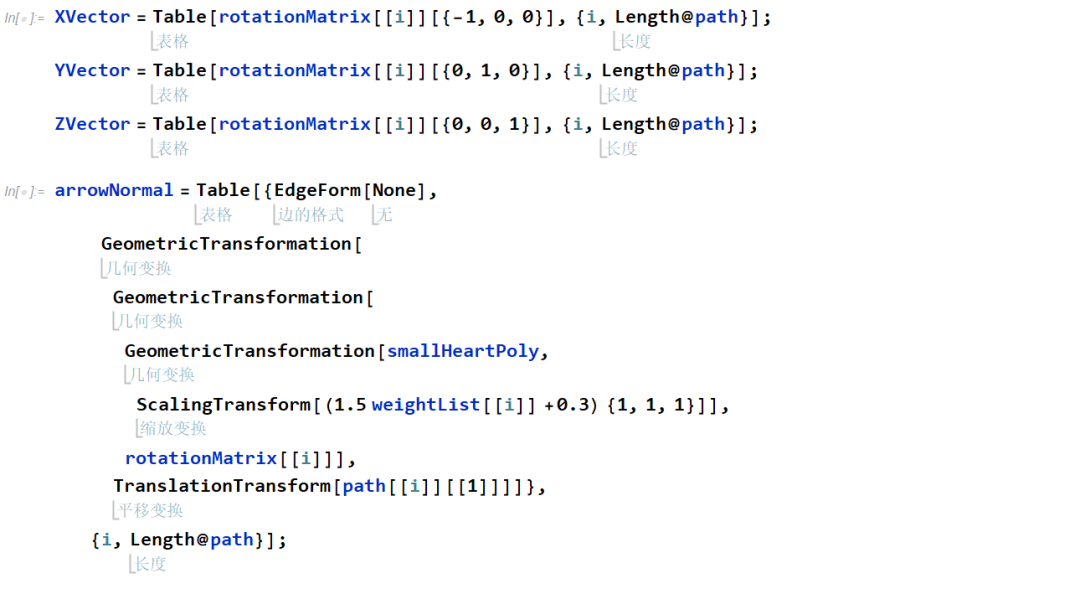
下图展示了叶子的坐标系和姿态,其中 x 方向同曲线的切向相反,y 方向同边界法向向量在正交面的投影方向相重合。
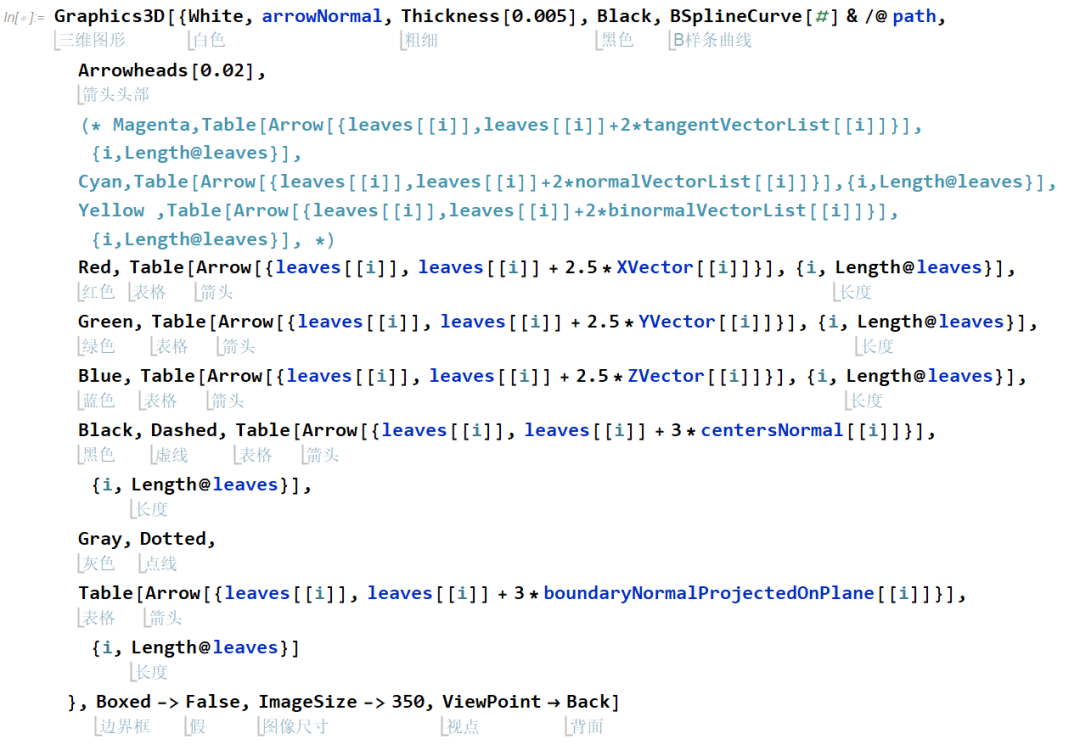

下图比较了两种叶子的坐标系和姿态,左图叶子姿态同移动坐标重合,右图在此基础上关联了 y 方向同边界法向。
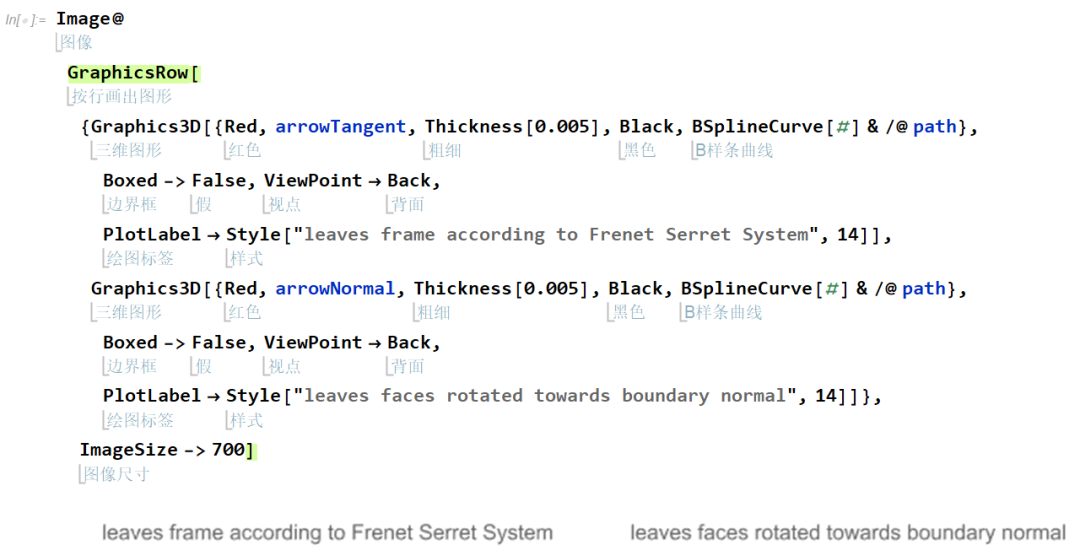
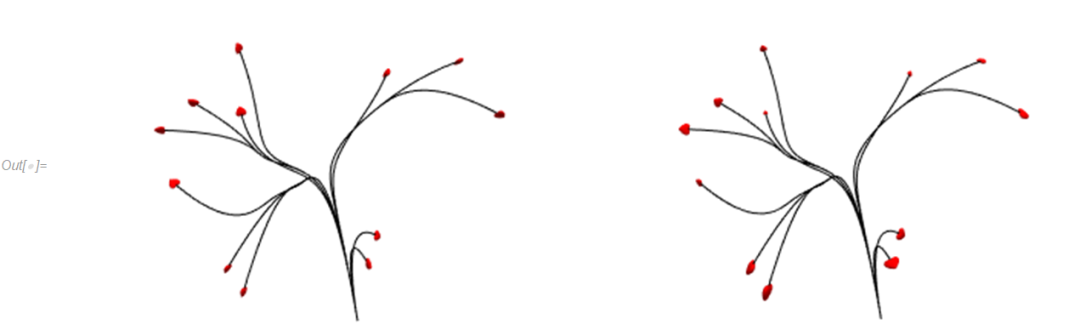

可视化
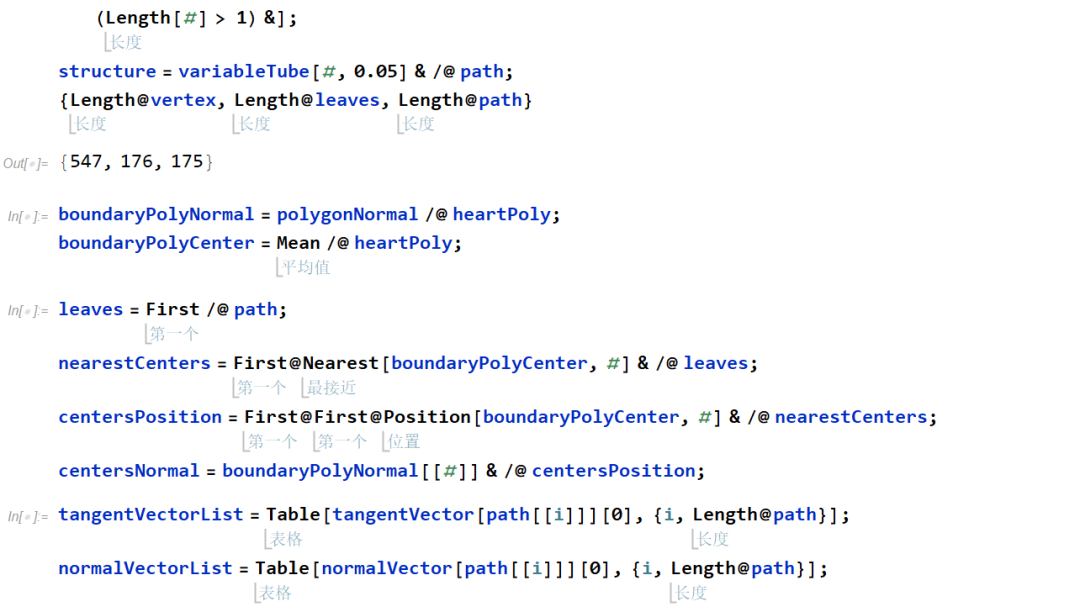
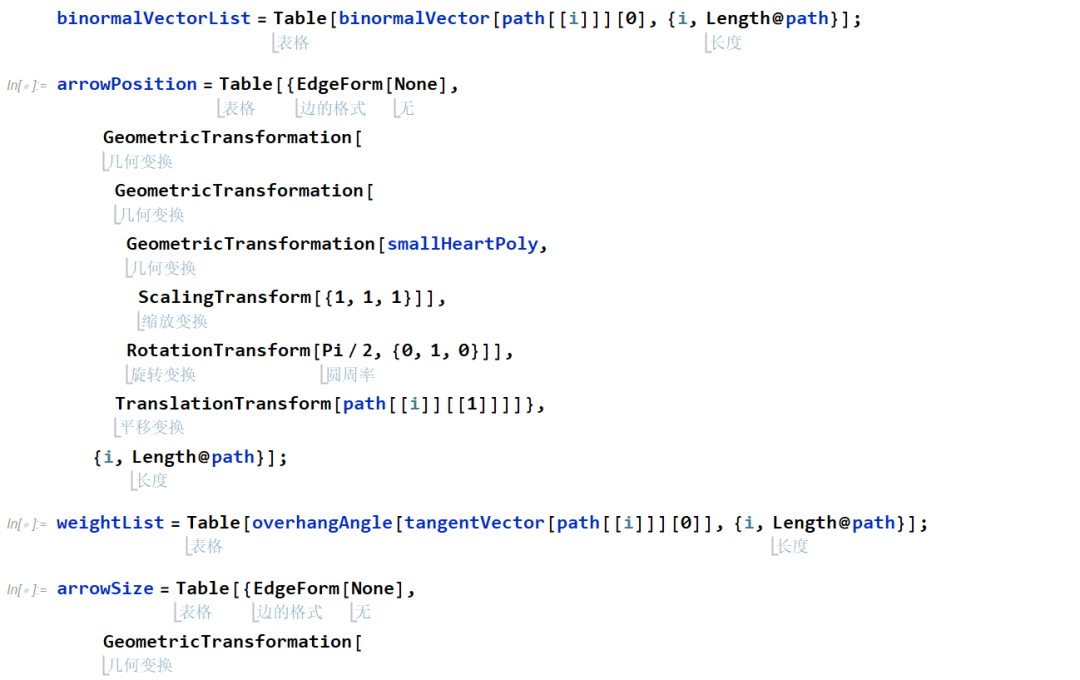
为了创建一颗生机勃勃的三维树,本章我们增加了顶点的数量共547个,其中包含1个根和 175 个叶。






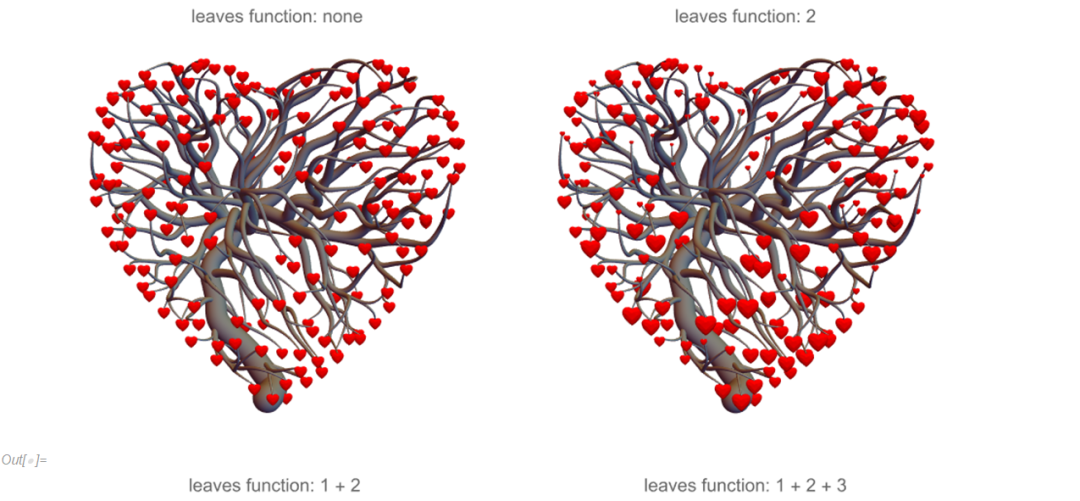
如下四图比较了三项不同的关联函数。其中
左上图中叶子的位置采用了树图中的笛卡尔坐标;
右上图中叶子的大小还采用了关联函数 2,叶子的尺寸同重力悬垂角关联;
左下图中叶子的姿态还采用了关联函数 1,叶子姿态同树枝切向关联;
右下图中叶子的姿态还采用了关联函数 3,叶子姿态同环境边界法向关联;
犹如莱布尼兹哲学断言,"树上没有两片完全相同的叶子。"
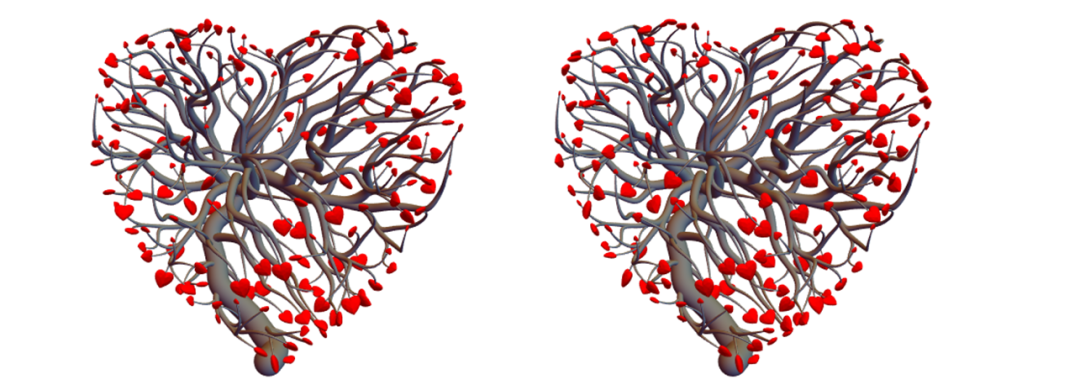
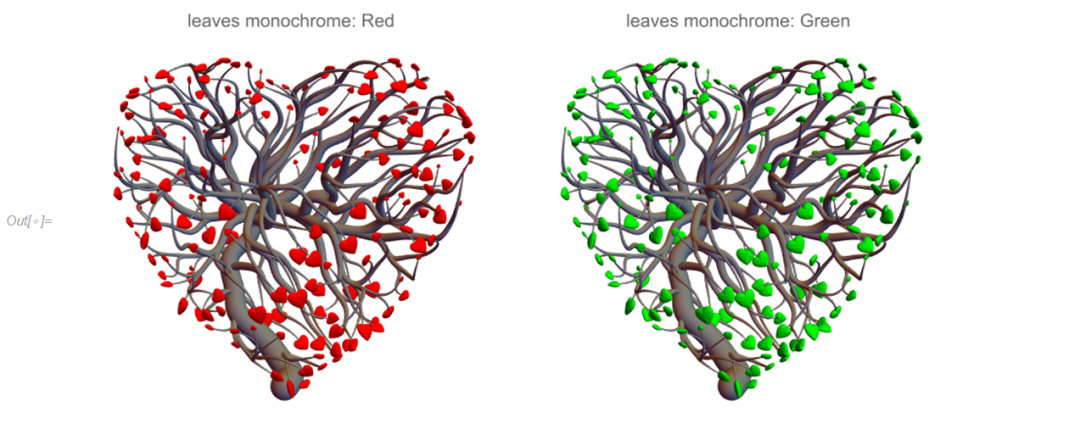
通过设置颜色,爱心树可以是一种经典红或植物绿。它们分别看上去有点像一大束花或者一盆绿色植物。
如果你还想再异域情调或者外星文明一点,可以设置不同的梯度渐变色。






变换
回到现实,现在这颗三维树模型可以说相当复杂。即使采用最先进的3D打印技术,直接制造这样一个三维模型仍有极高的制造风险。如果采用SLM工艺,底部支撑会把所有的树叶都毁了。如果采用MJP和失蜡法工艺,铸造时液态金属很难顺利地流过极细极小的树枝。所以我不得不在三维效果和可制造性之间进行妥协,后来我想到可以采用2.5维的浮雕方案,这样即不失模型的整体性,又可保留真实比例。
3D模型实际包含了足够的信息来生成深度映射或深度图 [4]。
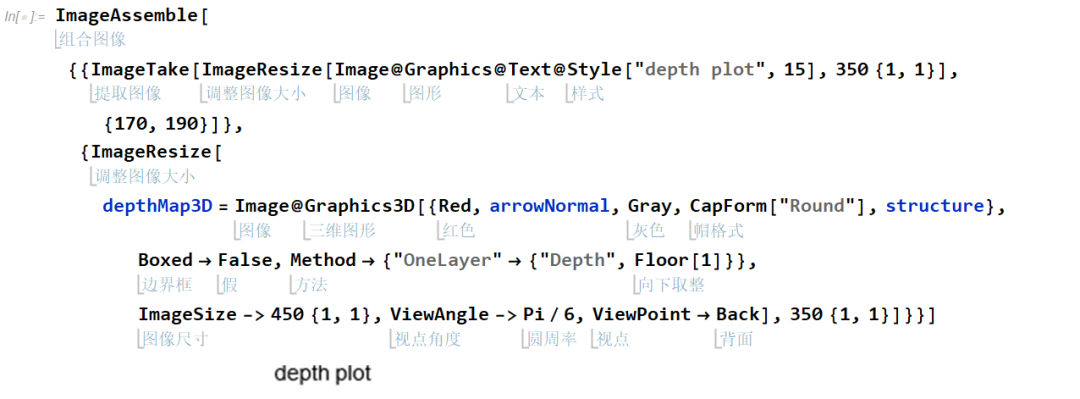

将深度函数在浮雕图上可视化,此处采用了一种插值方法 [5]。

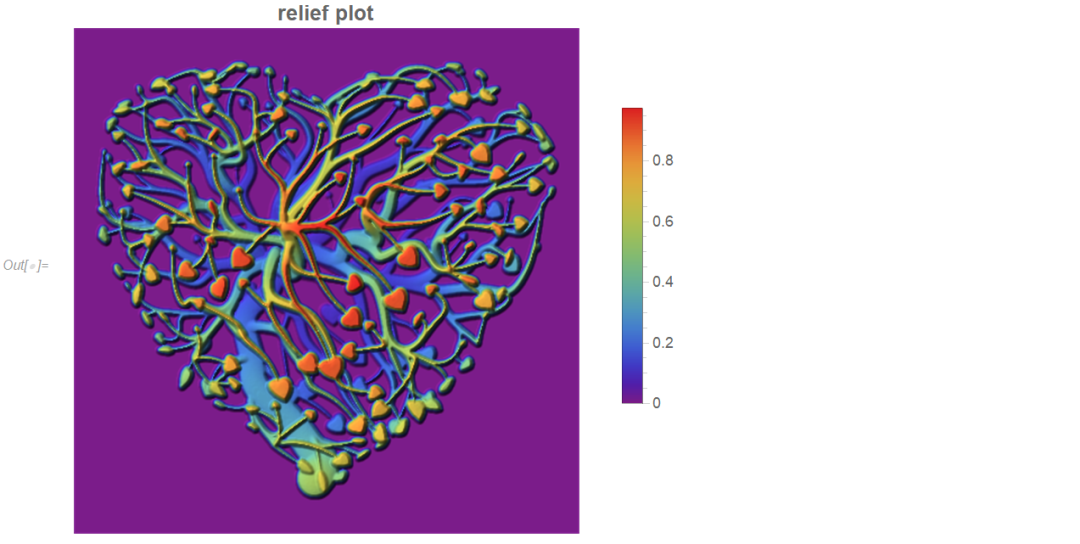
转换为浮雕图模型。

导出浮雕图模型。


渲染
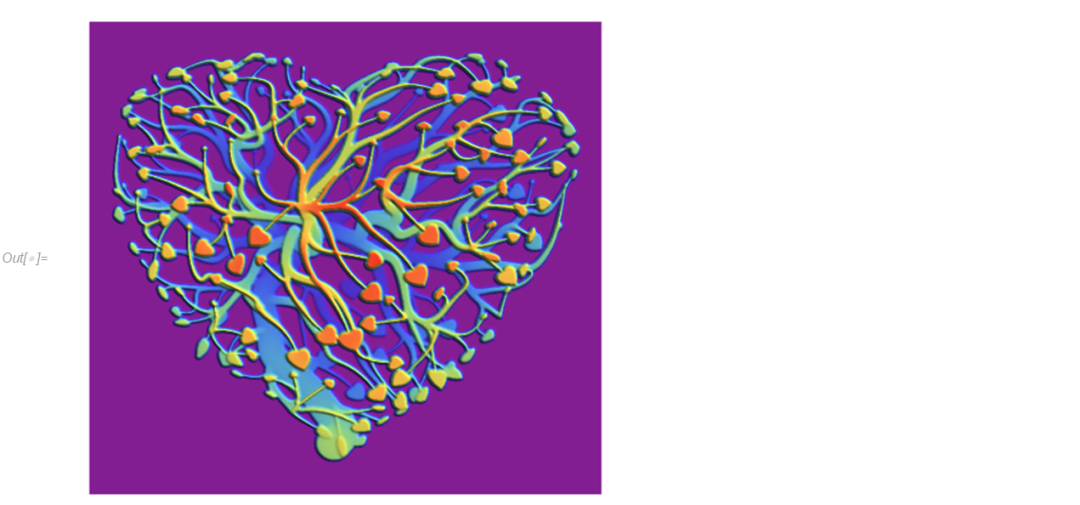
通过对STL模型边界,完成最终模型,并导入渲染。
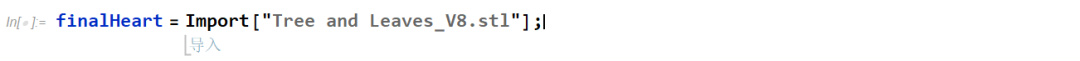
吊坠的正面图案是同之前的爱心树完全一样。背面图案是一颗抽象的树,我略过细节。你可以把它看作是一片叶子,叶子在微观尺度下就是一颗巨大的树。或者你也可以把它看作是心脏和心血管,或者是夜空中的一道闪电。它们都对,因为在计算机科学中它们都是树。


样品
新首饰样品诞生了!它采用 3D 打印(MJP工艺+失蜡法铸造),材料为银,尺寸大约1美元。表面经过抛光处理,随后电镀了玫瑰金。

项链吊坠是为女儿们准备的,因为在不远的将来她们极有可能会在元宇宙中发现一颗一模一样的爱心树。

回顾
全自动创建一颗三维爱心树;
基于最小生成树算法和施泰纳最小生成树算法;
采用B 样条曲线和Tube设计树干和树枝结构;
建立三个概念和函数来模拟自然界中的叶子状态;
计算B 样条曲线的 Frenet Serret 移动坐标系;
将叶子姿态同树枝切向相关联;
将叶子姿态同树的边界法向相关联;
将叶子大小同重力悬垂角相关联;
将三维模型转换为深度图和浮雕模型;
采用 3D 打印 MJP工艺+失蜡法铸造;
制造一枚双面图案的项链吊坠。
武汉墨光是光机电领域优质服务商,提供 SYNOPSYS™光学设计软件、ASAP高级光学系统分析软件、APEX光机系统分析与设计软件、JCMsuite 纳米光学仿真分析软件、PCGrate 光栅设计软件、RP Fiber Power 光纤激光器及光纤器件设计软件、Mathematica 科学计算软件 等产品的推广、销售、咨询、培训、技术支持、软件二次开发及解决方案等服务,辅助高校教学科研、研究所进行高端技术研发以及光机电厂商利用光学软件研发各领域的光学器件与光机系统,在最短时间内完成量产并获利。