【思想与探索|刘沛清】关于理想、可压缩流体、定常等熵流动问题研讨
风流知音(FLOWS:Physics & beyond)【思想与探索|刘沛清】关于理想、可压缩流体、定常等熵流动问研讨 CFDST(2022年12月8日)1054
刘沛清,人称沛公,1982年在华北水利水电大学获学士学位。1989年在河海大学获硕士学位,1995年在清华大学获博士学位。1997年至今,在北京航空航天大学流体所工作。2000年至今,任教育部流体力学重点实验室责任教授,博士生指导教师。2003年至2012年,任航空科学与工程学院副院长。现任中国空气动力学学会理事,中国力学学会流体力学专业委员会工业流体力学组组长。长期从事飞行器空气动力学实验和数值模拟等研究工作。《空气动力学》国家级精品课程负责人,国家级航空航天实验教学示范中心主任,空气动力学学报编委。现为北京航空航天大学陆士嘉实验室(航空气动声学工信部重点实验室)主任。

刘沛清教授
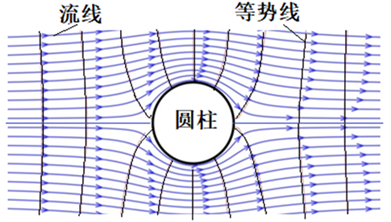

图1 理想不可压缩流体定常无旋圆柱绕流
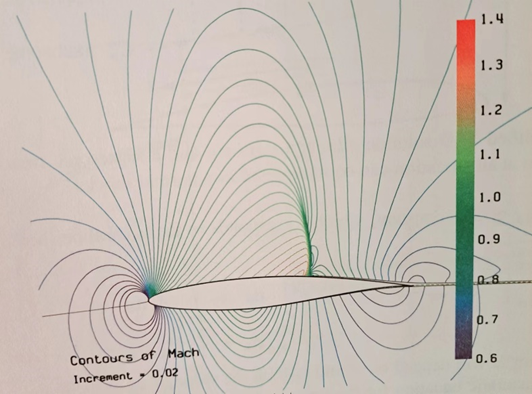

图3 理想可压缩流体定常无旋超声速翼型绕流
2、理想、可压缩流体、定常等熵流动控制方程
对于理想流体可压缩流体、定常等熵流动,控制方程为:
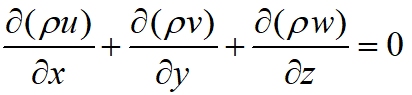
(2)不计质量力理想流体运动方程(欧拉方程组)
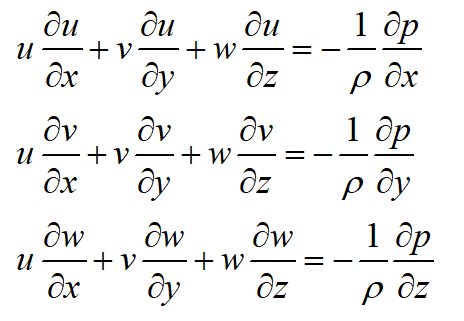
(3)理想定常等熵流动状态方程
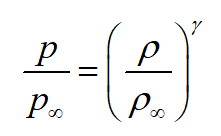
(4)理想定常等熵流动能量方程
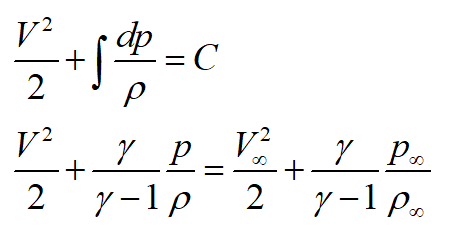
其中,
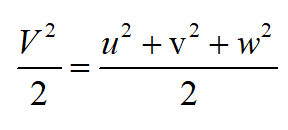
3、理想可压缩流体定常等熵无旋流动控制方程
(1)全速度势方程
利用等熵条件 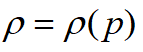 和波速方程
和波速方程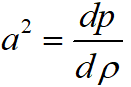 ,可得
,可得

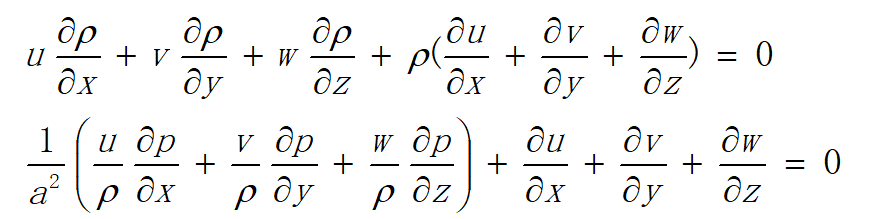
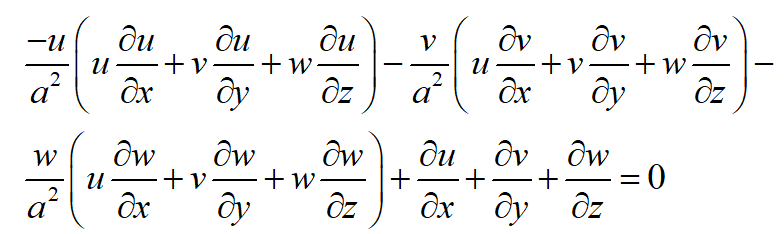

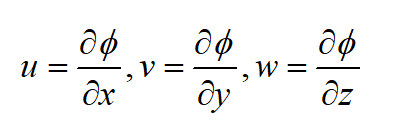
代入上述方程中,得
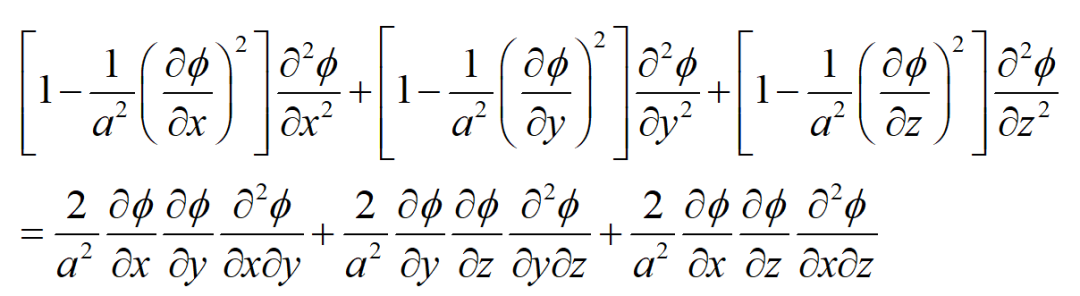
等熵流动的能量方程,有
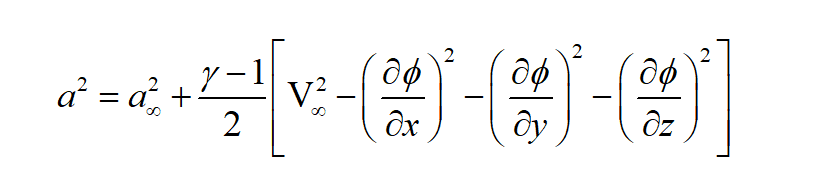
适应条件:
(a)分离流动,绕流物体分离尾流不满足无旋流动;
(b)出现强激波问题的绕流,不满足等熵流动;
(c)适应于所有马赫数范围。
(2)小扰动二阶速度势方程
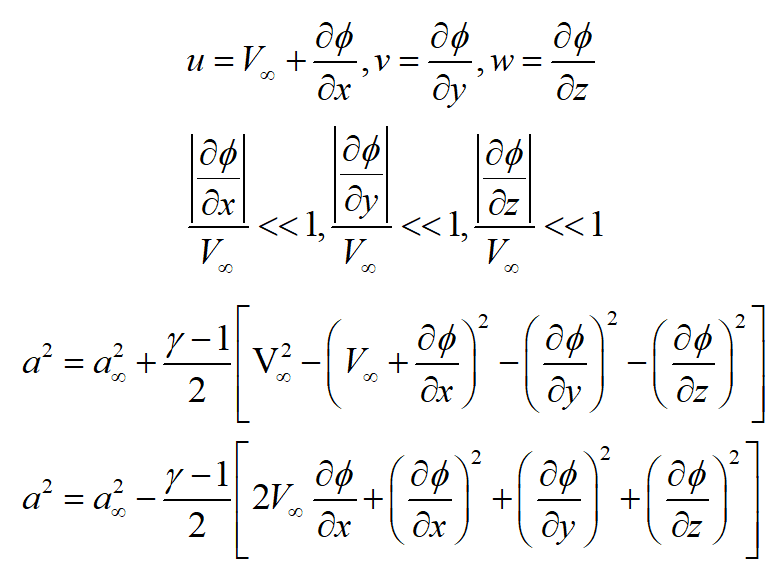
代入全速度势方程,保留二阶项,得到

(3)小扰动线化速度势方程
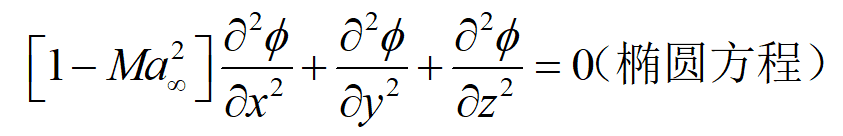
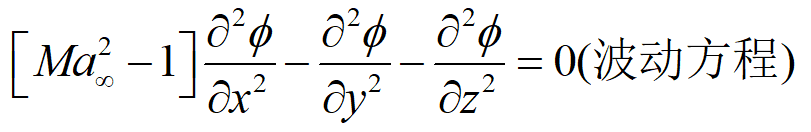
适应于小扰动(细长体)、小迎角超声速区,Ma∝>1.2。可以捕捉斜激波,计算激波阻力。

适应于细长体小迎角跨声速绕流。可以捕捉正激波和激波阻力。

适应于不可压缩势流。可以计算绕流物体升力。