用北京超算跑仿真是种什么样的体验?—结构篇
装配体处理起来相当耗时且计算量较大,因此在进行分析之前,一般需要根据项目周期,电脑性能,精度需求,处理难度等因素,综合平衡给出合适的前后处理方案
而在这些因素中,电脑性能无疑是人为最容易掌控的部分,毕竟只要肯花钱就能够极大的拓宽前处理的思路和方法
因此本文聚焦于电脑性能,期望通过典型案例的对比,得到影响结构计算的一些基本因素以及各自的影响程度,以帮助大家在进行有限元分析时,可以根据自身的需求选择合适的电脑性能以及求解平台
由于CPU核心数,内存大小这些基本参数是主要对比变量,为了获取足够多的数据点,需要准备一台内存足够大(200G+),核心数足够多(64+)的电脑作为对比计算的主要平台显然个人去组装这样一台高性能工作站的成本是较高的,因此联系到北京超级云计算中心(简称北京超算),对方也非常乐意提供平台给笔者进行算例测试,本次测试平台参数如下:(文末扫描二维码,免费试用)
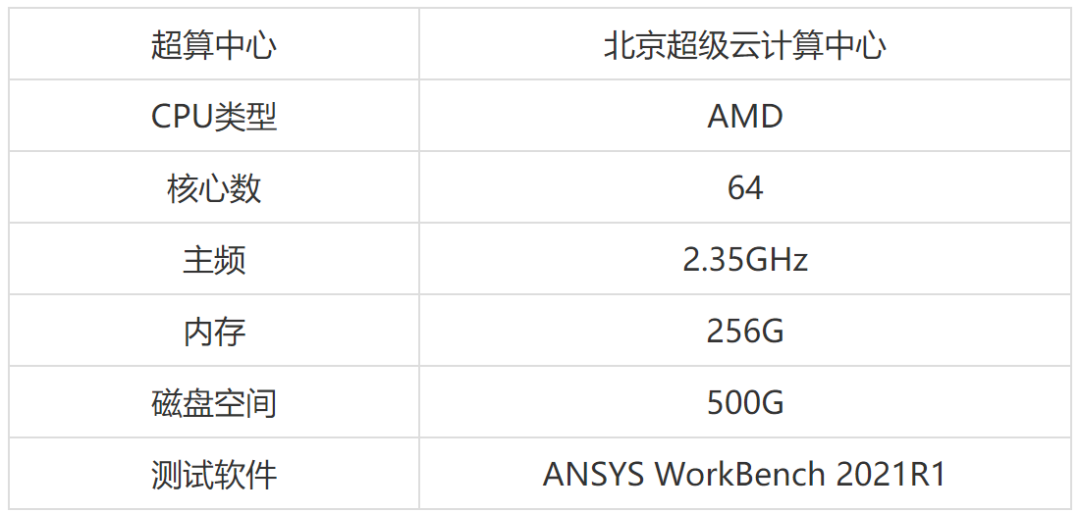
北京超级云计算中心可根据使用者需求提供不同型号CPU,核心数,内存大小以及磁盘空间,上述数据仅为本次测评使用参数。
常规结构分析有线性静力学,非线性静力学,模态分析,扫频分析,随机振动分析,谱分析,显式动力分析等,要同时一篇文章对比电脑性能对所有求解类型的影响显然不太现实
因此本文挑选其中最为典型的模态分析作为本次对比的基础分析模块,主要原因有两点:①模态分析相比于静力学分析计算量更大,考虑的结构因素更多 ②模态分析作为线性动力学分析体系核心中的核心,在大部分行业领域的结构分析中都不可或缺
同时为了减少接触,耦合,混合单元等对数据带来的“污染”,但是又不降低分析的通用性,选取典型的铸造轮毂作为分析对象,使用现在露脸频率最高的二阶四面体单元进行网格处理,如图所示(模型来源于GrabCAD):
综上,本文基于Ansys WorkBench 2021R1平台,使用北京超算中心,预期对比得到计算规模,核心数量,模态阶数,耦合方式等对模态分析内存使用和计算耗时的影响程度
由于模型的计算规模是最直接的影响分析内存消耗和求解时间的因素,而计算规模主要和整体模型的节点数量相关
因此在该部分对比中,将轮毂按照不同网格尺寸分别划分为10,20,40,80,160,320万节点数量,得到其对计算时长和内存占用的影响
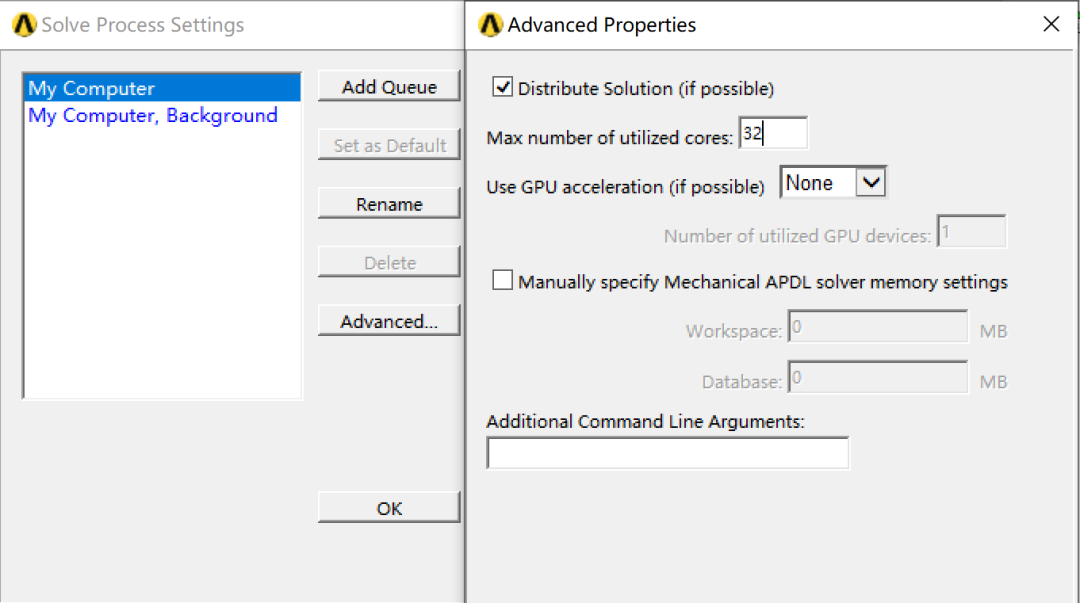
为保证数据的公平性,CPU核心数量设置为60,提取前100阶约束模态,特征值提取方法为Block Lanczos,其余参数默认

根据上述设置,对不同节点数量模型进行求解计算,统计其内存消耗:
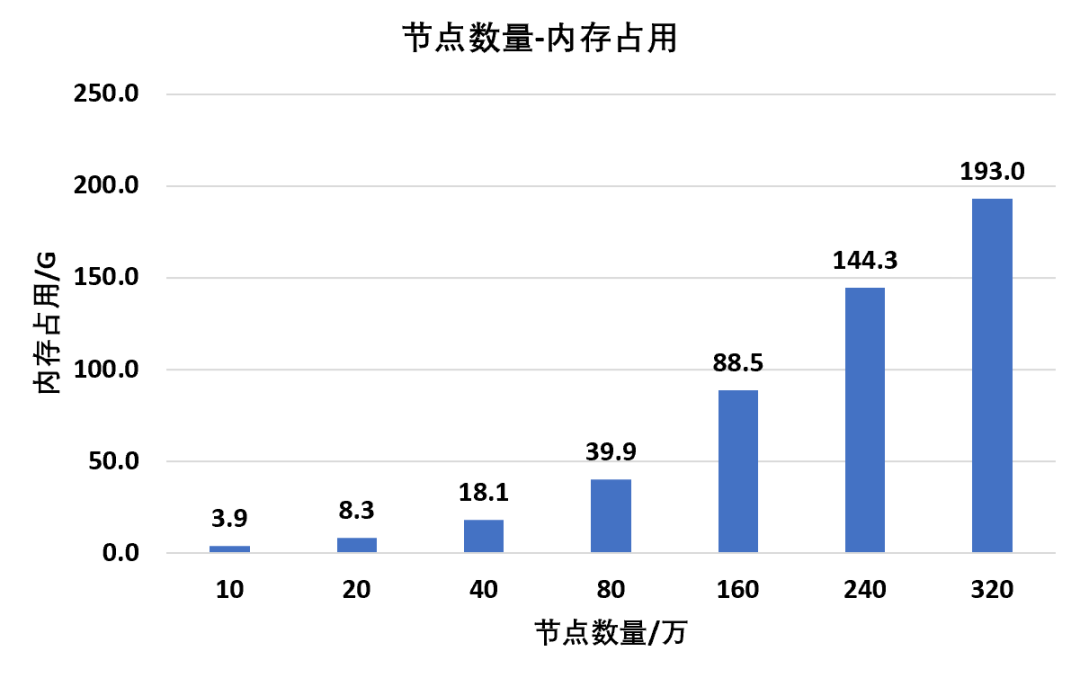
从整体规律上来看,随着节点数量的增多,内存的占用也会随之增大,并且当高阶四面体的节点数量达到160万时,内存占用已经达到88.5G
而一般个人台式机可以会选择四个槽口上插满16G的内存条,也就是总共64G内存,虽然看起来很多,但是已经表明普通台式机很难满足ansys百万节点级别的高阶单元动力学计算需求
为了更加清晰地得到节点数量和内存占用之间地关系,将上述数据按照基本数据归一化,得到节点数量比-内存占用比之的关系曲线: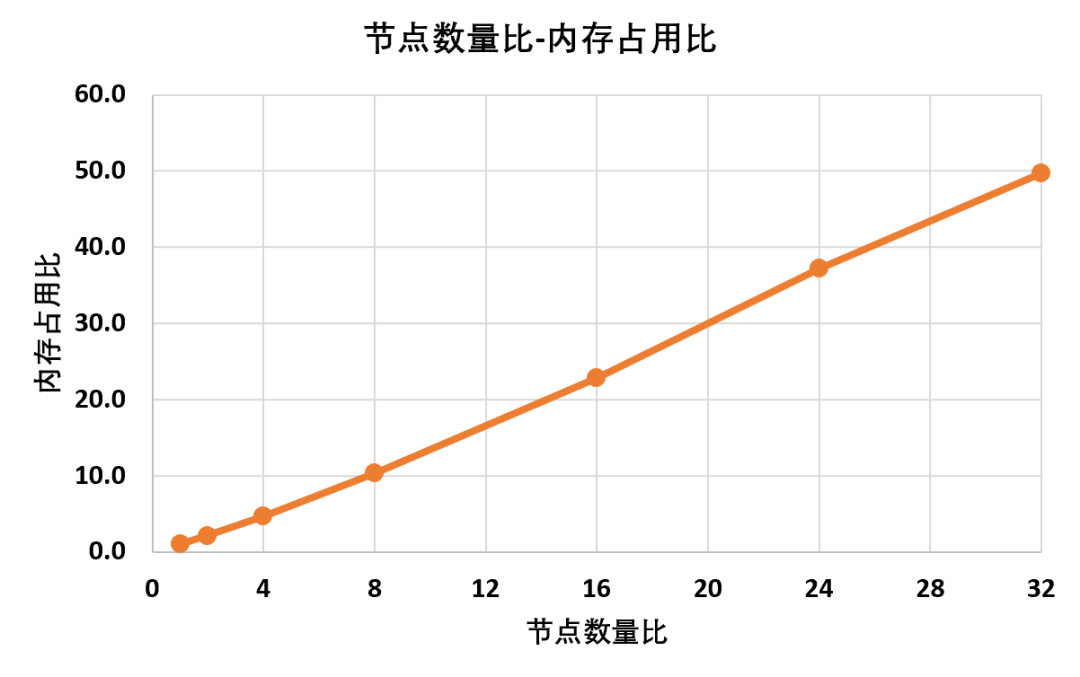
可以看到节点数量和内存占用之间基本是线性相关,但是并不是1:1增长,典型的节点数量增加32倍,内存占用增加了50倍
这样对于自己的电脑,只需要通过两个数据点,就能够大致估算出能够计算的最大节点数量。
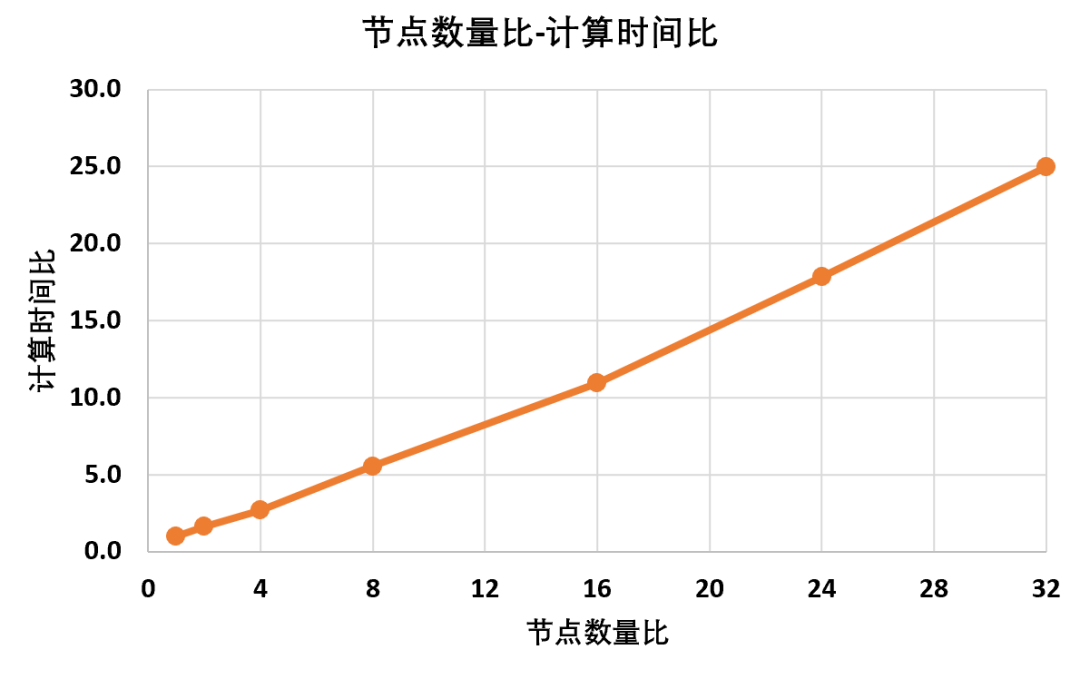
同时,统计不同节点数量下模型的计算时长以及归一化处理结果:
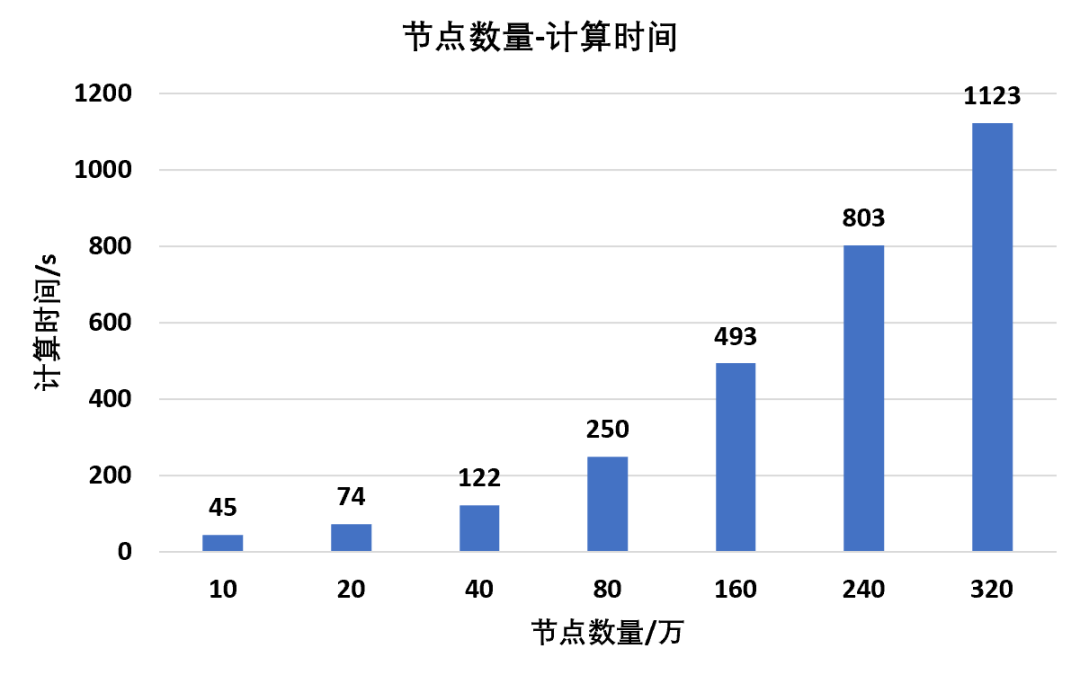
根据计算数据可以得到,随着节点数量的增加,模型的求解时间显然是逐渐变长,并且根据曲线所示,他们之间同样存在着线性比例关系同样这种关系并不是1:1,典型的节点数量比例增加32倍,计算时间同等情况下增加25倍求解器在物理内存已经不满足计算需求之后,会调用一定的虚拟内存,虽然电脑还能勉强计算,但是求解效率会大大降低,计算时间也会不符合上述线性规律
核心数量影响
显然通过降低总的节点数量可以极大程度降低求解时间,但是对于复杂装配体,节点数量其实很难降下来,这个时候我们会寄希望于多核并行
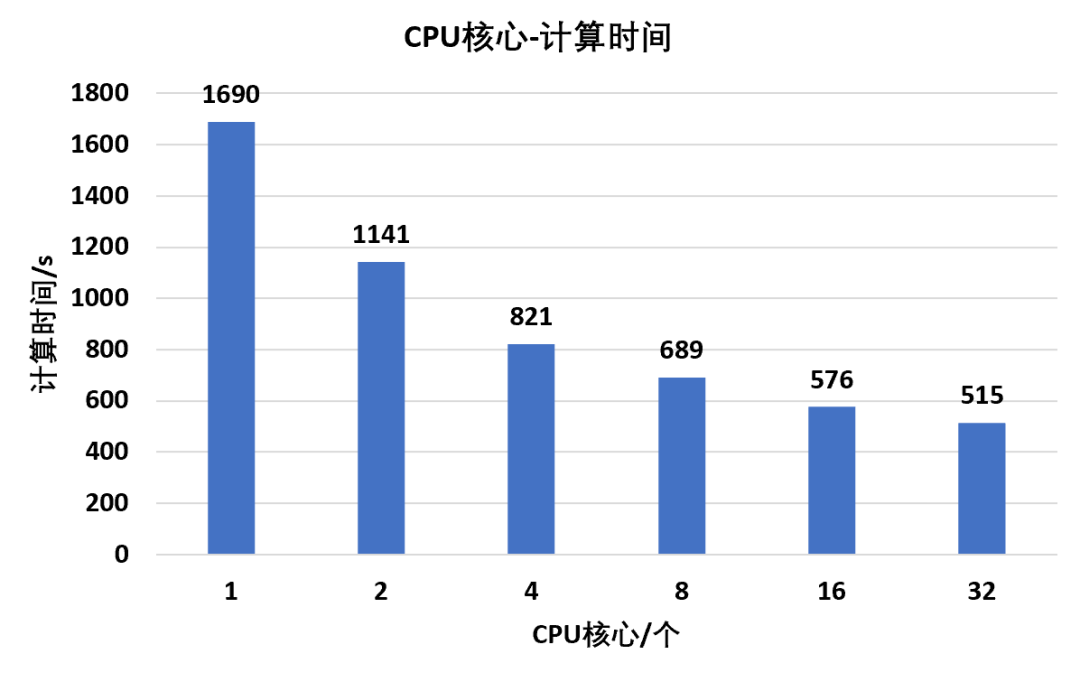
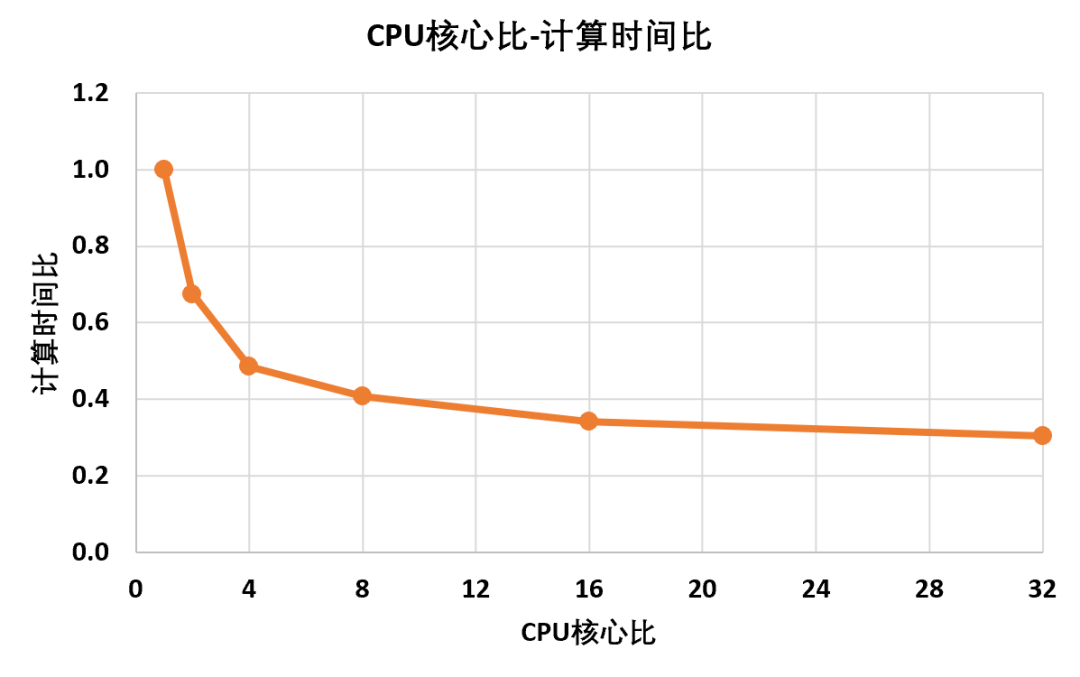
因此该部分中,将求解核心数分别设置为1,2,4,8,16,32核,来对比不同核心数下求解时长的变化同样为了保证数据对比的合理性,选择前文160万网格规模模型,模态提取阶数依然为100阶,特征值提取方法为Block Lanczos,其余参数默认按照同样方法,对不同核心数下计算时长进行统计并归一化处理:根据统计数据结果可以得到,CPU核心并行数量和计算时间呈现一种非线性关系即在最开始1核心→2核心→4核心时,计算时间的提升是可喜的,但是继续增加到8核心,提升幅度开始降低,到达16核心之后,基本上再提高并行核心数量,求解时长也没有降低太多根据曲线结果,从单核心到多核并行,结构分析的求解效率大致会稳定在0.25左右,也就是缩短75%的计算时长该结论仅为本文隐式结构分析的大致对比结果,但是显式分析,流体分析等由于算法的不同,会呈现不同的并行效率规律
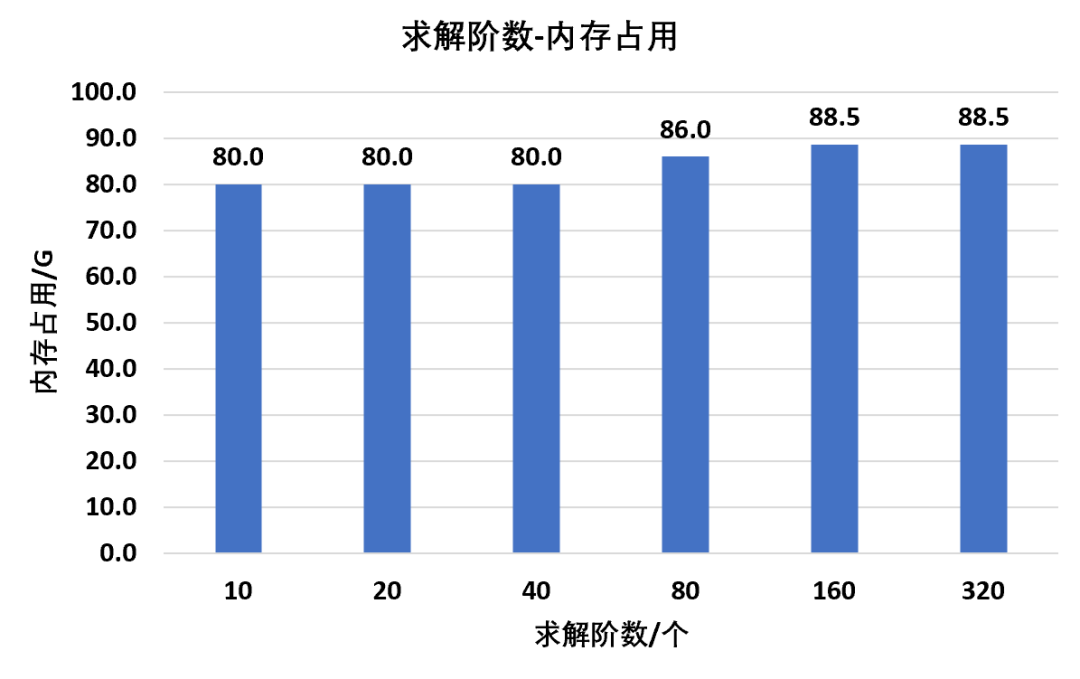
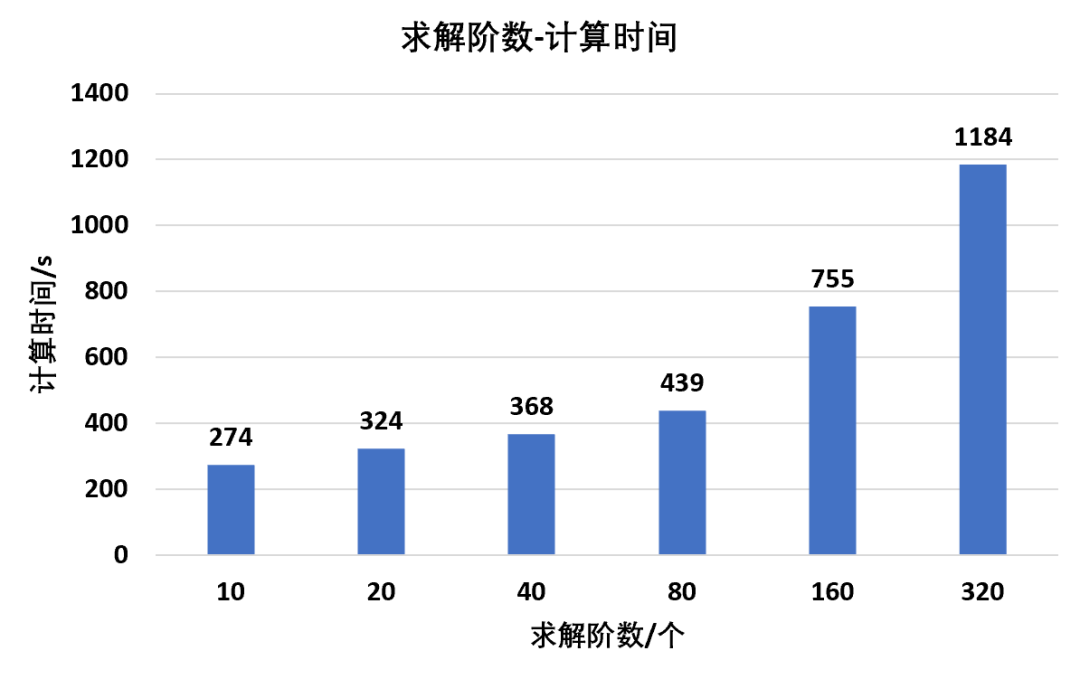
对于模态分析,有时候初次计算需要提取大量的模态阶数,再从中筛选出关注的模态结果,这个时候就会遇到一个问题提取过多的模态阶数是否会对内存和计算时长产生更多的需求?为了研究这一问题,针对上述160万节点规模模型,分别设置模态提取阶数为10,20,40,80,160,320阶,得到其对内存占用和求解时长的影响同样选择Block Lanczos算法,并行核心设置为60,其余参数默认统计不同模态阶数下求解器的内存使用情况,并对结果进行归一化处理如下:根据统计数据可以得到,从1阶到320阶,虽然总体上求解阶数的增加会增加部分内存需求,但是比例上影响较小,基本可以忽略同样统计不同模态阶数下求解器的计算时长,并对结果进行归一化处理如下:根据上述统计结果,随着求解阶数的增多,整体趋势上计算时间是逐渐增加,但是存在一定的波动,线性关系不是非常完美并且和预想的不同,模态阶数从10阶增加到320阶,计算时间并没有直接变为原来的32倍,而是变为4.3倍也就是说,虽然模态提取阶数越多,求解时间越长,但是比例上小很多(本例仅1/74),并不是1:1的增加模态提取算法有多种,该部分仅为Block Lanczos算法得到的统计数据,并不代表所有模态算法均是如此
耦合方式影响
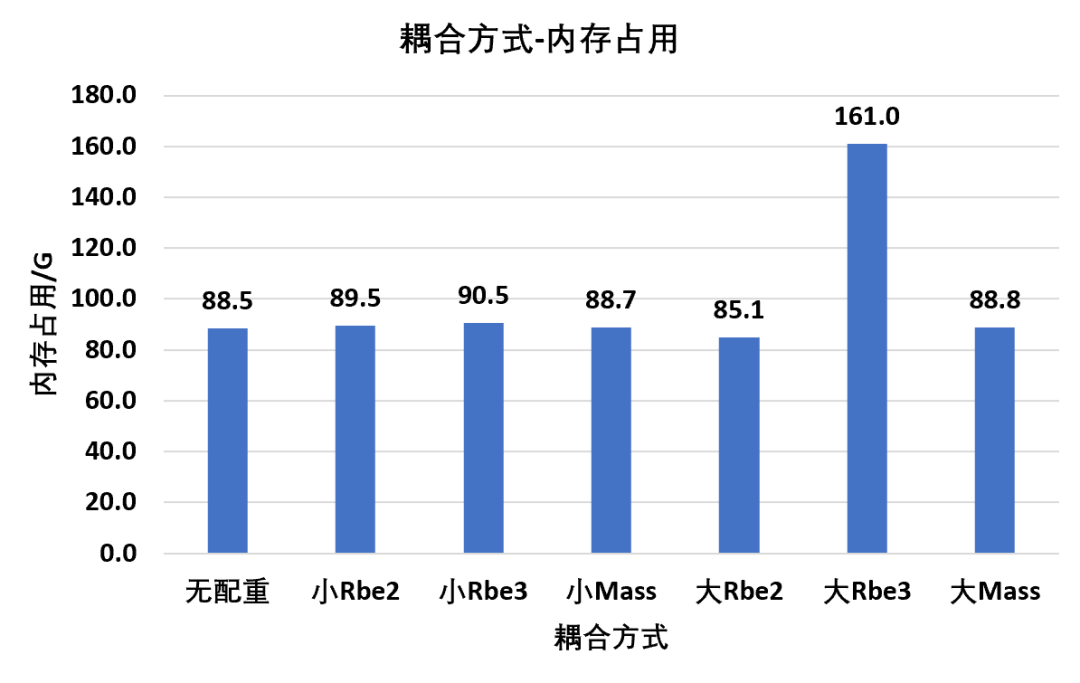
耦合(更加专业的说法为多自由度约束)在装配体分析中应用非常多,螺栓,胶粘,焊缝,配重,运动副等各个地方都会用到作为独立于共节点,绑定接触的第三种连接方式,耦合非常方便使用,因此也很容易出现滥用的情况本文不讨论不同耦合方式的精度问题,仅仅就其对计算时间和内存占用这部分的影响进行对比该部分以配重为典型,分别对比耦合面积小,耦合面积大,以及Rbe2,Rbe3,Mass三种方式,共六种组合下的计算情况:其中集中配重中的Rigid指Rbe2方式,集中配重中的Deformation指Rbe3方式,分布配重指质量点直接均布Mass方式同样统一设置CPU核心数60,提取阶数100,提取方法Block Lanczos通过统计结果可以得到,几种配重方式中,小面积配重由于涉及到需要分配自由度的节点数量不多,因此不会带来过多的额外内存需求但是大面积配重时,Rbe2和Mass由于处理方式的原因,也不会带来过多的内存附加,但是Rbe3由于属于一种柔性的多点约束方式,需要在各节点之间进行自由度分配,因此会导致过大的附加内存需求通过统计结果可以得到,Rbe2和Mass方式不管在小面积还是大面积耦合,同样不会带来过大的附加计算时间但是Rbe3方式在大面积耦合时显然会带来非常多的附加计算,导致计算时间远远高于其余处理方式上述仅单纯计算时间和内存占用的对比,并不代表哪种方式在实际使用时的精度对比
根据本文中对比数据,大致可以得到以下几点规律和建议:①节点数量是影响求解过程中内存占用和计算时长的最主要因素,因此当电脑性能不足时,首要考虑的是简化模型(分析类型固定情况下)②动力学求解高阶节点数量达到百万级别时,普通台式机内存已经很难满足计算需求,此时建议寻求超算平台帮助;③模态求解设置较多(本文320阶)提取阶数,并不会增加过多的内存需求,但是会以一定比例增加计算时长,因此模态计算阶数的设置可以不用过于谨慎④在大面积耦合时使用Rbe3需要格外注意其带来的附加内存需求和计算时长,此时一般建议将质量分布在几个小面处理
⑤本文并未提到,但是大家在使用过程中一定会感受到,绑定接触的大量使用同样会导致极大的附加计算量,因此不可滥用