基础:差分对与差分阻抗
基础:差分对与差分阻抗
1 基本概念
差分对:指一对存在耦合的传输线。
差分信号:当驱动器在传输线上驱动一路信号时,在信号线和返回路径之间会存在一个信号电压,通常称之为单端传输线信号。当两路驱动器驱动一个差分对时,除了各自的单端信号外,这两路信号线之间还存在着一个电压差,称之为差分信号,如图 1 所示:

差分信号用公式表示为:
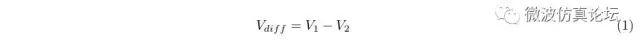
式中,V diff 表示差分信号,V 1 表示线 1 相对于共用返回路径的信号电压,V 2 表示线 2 相对于共用返回路径的信号电压。
共模信号:用两条信号线上的平均电压表示,用公式表示为:

式中,V comm 表示共模信号,V 1 表示线 1 相对于共用返回路径的信号电压,V 2 表示线 2 相对于共用返回路径的信号电压。

2 差分对的差分阻抗
差分对对差分信号的阻抗即为差分阻抗(Differential Impedance),它是差分信号电压与其电流的比值,这个定义是计算差分阻抗的基础。
2.1 无耦合时的差分阻抗
先分析构成差分对的两条传输线之间不存在耦合时的差分阻抗。为了使耦合降到最小,假定两条传输线离得足够远(线距至少为线宽的 2 倍),这样它们之间的相互作用就不明显。
设每根线的单端特性阻抗为 Z 0 ,流经信号传输线与返回路径之间的电流为:

式中,I one 表示流经信号线与返回路径的电流,V one 表示信号线与邻近返回路径间的电压,Z 0 表示单端信号线的特性阻抗。
根据阻抗的定义,差分信号的阻抗可以表示为:

式中,Z diff 表示信号线对差分信号的阻抗(即差分阻抗),V diff 表示差分信号电压,I one 表示流经每根信号线与其返回路径间的电流,V one 表示每根信号线与其邻近返回路径间的电压,Z 0 表示每根线的单端特性阻抗。
上式表明差分阻抗的大小是单端信号线特性阻抗的 2 倍,也就是说差分阻抗可以看做两个单端信号线等效阻抗的串联,如图 2 所示。

2.2 有耦合时的差分阻抗
当两传输线相距很远时,线 1 的特性阻抗完全不受另外一根线 2 的影响。当差分线对中的两条线逐渐靠近时,它们的边缘电场和磁场就会相互影响,两线之间的耦合程度也就越来越强。这时线 2 的存在将会影响线 1的阻抗,称之为邻近效应。此时信号线 1 的特性阻抗不是一个特定的值,它还取决于临近信号线 2 的驱动情况。如果信号线 2 被固定在 0 电位,则信号线 1 的特性阻抗值接近于未耦合时的值;如果信号线 2 加与信号线 1 相反的信号,则信号线 1 的特性阻抗值就会降低;如果信号线 2 加与信号线 1 相同的信号,则信号线 1的阻抗值就会升高。图 3 给出了这三种情况下,信号线 1 的单端特性阻抗随两信号线间距的变化情况。
当差分信号沿差分对传输时,对它来说,总的阻抗是每根信号线与其返回路径间单端特性阻抗的串联。


Figure 3: 当分别给第 2 根信号线加 0 伏电压、相反信号、相同信号时,线 1 的单端特性阻抗随两线间距的变化情况。传输线为 5mil 宽、50Ω 的 FR4 基板带状线,使用 Ansys Q3D 仿真得到。
2.3 差分阻抗的计算
当信号线间距越来越小并且耦合开始起作用时,差分阻抗就会逐渐减小。总体来说有 5 种方法计算阻抗值的变化情况:
• 使用近似公式得到结果;
• 使用场求解方法得到结果;
• 使用基于模态分析方法得到结果;
• 使用基于电容和电感矩阵分析方法得到结果;
• 使用基于特性阻抗矩阵分析方法得到结果。
计算边缘耦合微带线或者是带状线的差分阻抗,目前只有一种有用且合理的近似方法。它最早由 JamesMears 在国际半导体应用手册(AN-905)中给出。这种近似方法是基于实验数据得到的经验公式。
对于以 FR4 为基板材料的边缘耦合微带线,差分阻抗近似为:

式中:Z diff 表示差分阻抗(单位为 Ω)、Z 0 表示未耦合时的单端特性阻抗(单位为 Ω)、s 表示信号线的边沿间距(单位为 mil)、h 表示介质基板的厚度(单位为 mil)。
对于以 FR4 为基板材料的边缘耦合带状线,差分阻抗近似为:

式中:Z diff 表示差分阻抗(单位为 Ω)、Z 0 表示未耦合时的单端特性阻抗(单位为 Ω)、s 表示信号线的边沿间距(单位为 mil)、s 表示上下地平面间介质基板的厚度(单位为 mil)。
通过与精确的场求解方法计算得到的差分阻抗相比较,可以发现上述两个近似公式的误差在 1% 到 10% 之间。如图 4 所示:


Figure 4: 将由近似公式得到差分阻抗与二维场求解器得到的结果相比较。图中线宽为 5mil,基板材料为 FR4。图中实线表示近似公式的结果,虚线是由 Ansys Q3D 仿真得到的结果。
3 奇模和偶模
差分对的驱动端可以加上任何电压。然而对于耦合微带线和带状线差分对来讲,有两种特殊的电压模式可以实现无失真的信号传输。第一种是给两条信号线加相同的信号,第二种是给两条信号线加相反的跳变信号。这两种沿差分对无失真传播的信号电压模式对应了差分对被激励的两种特殊状态,称之为差分对的模态(mode)。为了区分这两种状态,我们称两线上有相同的驱动电压的模态为偶模(Even mode),两线上有相反的驱动电压为奇模(Odd mode)。

模态是指差分对的固有性质。当然任何电压模式都可以加到一对传输线上,但只有符合这两种状态的一种时,传输的电压信号才具有上述特性。差分对的模态是用来定义特殊电压模式的。
当组成差分对的两条导线具有几何对称性,并且线宽和介质间距相同时,激励偶模和奇模的电压模式分别对应于两线间加相同和相反的电压。如果两条导线不具有对称性,偶模和奇模的电压模式就不是这样简单了。确定它们的唯一方法就是使用场求解器。图 5 给出了对称导线对的奇模和偶模状态下的场模式。
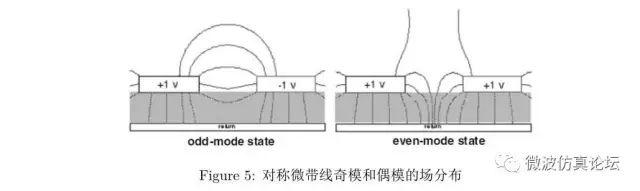
一方面模态的定义是指信号线对特殊的激励状态,它以信号线对的几何外形为基础;另一方面驱动电压可以为任何值,任何电压模式都可以加到信号线上,只需在信号线与返回路径间加上一个函数发生器即可。

引入奇模和偶模的概念后,就可以用它来标记一个对称的差分对的特性。对于一根信号线的阻抗,当差分对被驱动成奇模时称之为奇模阻抗,当差分对被驱动成偶模时称之为偶模阻抗。

3.1 差分阻抗和奇模阻抗
如前所述,差分阻抗是每根信号线与公共返回路径之间阻抗的串联。当不存在耦合时,它的值为每根信号线特性阻抗的 2 倍。当两条线间距很小时,耦合就变得比较重要,此时每根信号线的特性阻抗都会改变。
当差分信号加在差分对上时,差分对处于奇模状态。根据定义,此时每根信号线的特性阻抗被称为奇模特性阻抗。如图 6 所示,差分阻抗是奇模阻抗的 2 倍。因此差分阻抗为:
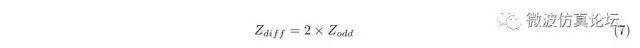
式中,Z diff 表示差分阻抗,Z odd 表示当差分对处于奇模状态时每根信号线的特性阻抗。

Figure 6: 当以差分信号激励差分对时,每根信号线与返回路径之间的阻抗就是奇模阻抗,差分阻抗就是两信号线间的等效阻抗。
可见,奇模阻抗与差分阻抗有着直接的关系,但二者并不相同。计算或测量差分阻抗的方法就是先计算或测量出单个线的奇模阻抗,再将其乘以 2。
3.2 共模阻抗和偶模阻抗
共模信号是两信号线电压的平均值。纯共模信号是不与差分信号共存的,它是指在两信号线上加相同的电压。
共模信号使差分对处于偶模状态。根据定义,当传输线上传输共模信号时,每根信号线的特性阻抗被称为偶模特性阻抗。对共模信号来说,共模阻抗是每根信号线偶模特性阻抗的并联。如图 7 所示,两个偶模阻抗的并联阻抗为:

式中,Z comm 表示共模阻抗,Z even 表示当差分对处于偶模状态时每根信号线的特性阻抗。

Figure 7: 当以共模信号激励差分对时,每根信号线与返回路径之间的阻抗就是偶模阻抗,共模阻抗就是两信号线与返回路径平面间的等效阻抗。

设有一个边缘耦合的微带传输线对,基板材料为 FR4,线宽 5mil,无耦合时的特性阻抗为 50Ω。图 8 中列出了用场计算器计算出来的所有四种阻抗。可见,随着信号线间距的减小,耦合度增加,奇模阻抗减小,差分阻抗也随之减小。同时偶模阻抗增加,共模阻抗也随之增加。在这个例子中,在可制造的最紧密耦合线间距下,差分阻抗和共模阻抗受耦合的影响依然很小。耦合最紧密时,差分阻抗仅减小了 10%。

Figure 8: 间距增加时,所有与边缘耦合微带线对相关的阻抗变化情况。使用 Ansys Q3D 仿真。
4 奇模和偶模的传输速度
用奇模和偶模两种传输模态分量来描述信号的方法对边缘耦合微带线非常重要,因为在边缘耦合微带线上不同的模态的传播速度不同。
信号沿传输线的传播速度是由电场穿过介质的有效介电常数 ε eff 来决定的。根据电磁场理论,有效介电常数 ε eff 越大,该模态的波的传播速度就越慢,以该模态传输的信号的时延就越大。
图 9 给出了对称微带线和带状线的奇模和偶模的场分布。
对于带状线来说,导体周围的介质材料是均匀的,有效介电常数总等于体介电常数,与电压模式无关。因此在带状线中,奇模和偶模的传播速度是相等的。

对于微带线来说,由于电场一部分处于介质中,一部分处于空气中,因此有效介电常数是介质和空气介电常数的复合值。场分布的精确模式和覆盖介质材料的方式都会影响最终的有效介电常数 ε eff 和信号的实际传播速度。在奇模方式下,大部分电场分布于空气中;偶模方式下,大部分电场处于介质中,因此奇模比偶模有一个稍微小一点的有效介电常数。差分信号激励奇模传输而共模信号激励偶模传输,所以差分信号比共模信号的传输速度更快。图 10 中给出了这两种信号不同的传播速度。随着两线间距的增加,两线间的耦合度减小,奇模和偶模的场分布就会趋于相同。如果二者的场分布相同,那么每种模态都会有相同的有效介电常数和传播速度。

Figure 10: 奇模和偶模的传播速度。传输线为边缘耦合微带线,基板材料为 FR4,线宽为 5mil,阻值约为50Ω。
5 奇模和偶模阻抗的测量
时域反射计(TDR)可以用来测量单端传输线的单端特性阻抗。TDR 给传输线加上一个阶跃电压,然后测量反射电压。反射电压由下式确定:

式中,ρ 表示反射系数,V reflected 表示用 TDR 测量出的反射电压,V incident 表示 TDR 加在传输线上的电压,Z 0 表示传输线特性阻抗。
知道了输入电压再测出反射电压,就可以用下式计算出传输线的特性阻抗:

这就是测量任意单端传输线特性阻抗的方法。为了测量差分对中一根线的奇模阻抗和偶模阻抗,必须要在奇模或者偶模状态下测出相应的传输线的特性阻抗。为了激励差分对进入奇模状态,要给差分对加上差分信号,此时每根线的特性阻抗就是它的奇模阻抗。同样测量偶模特性阻抗时,要给差分对加上共模信号。
要实现这些测量需要一种特殊的带有两个信号源的 TDR,称为差分 TDR 或 DTDR。在 DTDR 中,两路的反射电压都可以测量出来,所以差分对中两条线的奇模和偶模特性阻抗也都可以测量出来。图 11 给出了一个测量差分对中一根线的奇模和偶模特性阻抗的实例。本例中的测试对象是一对紧密耦合的单端阻抗约为 50Ω的传输线,测得的单根传输线的奇模特性阻抗为 39Ω,偶模特性阻抗约为 50Ω。


Figure 11: 测试采用带有 DTDR 选件的 Agilent 86100 数字通信分析仪、TDA Systems IConnect 软件以及GigaTest Labs 探针台 完成。
6 参考文献
1. Eric Bogatin, Signal and Power Integrity-Simplified, Prentice Hall PTR, 2009.
2. Spartaco Caniggia, Francescaromana Maradei, Signal Integrity and Radiated Emission of High-Speed
Digital Systems, Wiley, 2008.
3. David M. Pozar, Microwave Engineering, Wiley, 2011.
本文来自《微波仿真论坛》,如有侵权请联系小编删除。




