CFD模拟过程中常见湍流模型介绍
本文摘要(由AI生成):
文章探讨了湍流的概念、形成过程及流体特性,并深入研究了湍流模型和壁面函数在数值模拟中的应用。湍流是流体流动的常见现象,分为层流区、过渡区和湍流区。层流可通过稳态Navier-Stokes方程预测,而湍流需借助瞬态方程。在数值模拟中,湍流模型和壁面函数用于处理近壁面流动。壁面函数虽能节省计算时间,但在高粘性流动中不适用。CFX软件提供了三种壁面函数选择,以适应不同场景。
湍流介绍:
如下图所示。匀速流体接触到平板的前缘,开始形成一个层流边界层。该区域的流动很容易预测。经过一段距离后,边界层中开始出现较小的混沌振荡,流动开始转变为湍流,并最终完全转变为湍流。
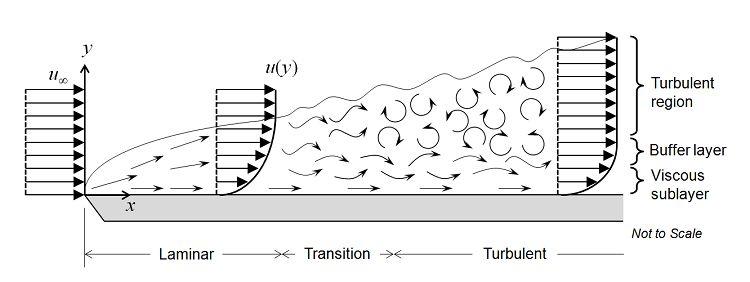
三个区域间的转变可通过雷诺数Re=ρvL/μ定义,其中 ρ 是流体密度,v 为速度,L为特征长度(本例中为与前缘处的距离),μ为流体的动态粘度。我们假定流体为牛顿流体,这意味着粘性张力与剪切速率直接成正比,比例常数为动力粘度。对于诸多颇具工程应用价值的流体,比如空气或水,实际情况的确如此或近乎如此。密度会根据压力变化,尽管通常认为流体为弱可压缩,即马赫数小于0.3,密度也会根据压力变化。
在层流区,流体流动可以通过求解稳态 Navier-Stokes 方程得到完全预测,其中预测了速度及压力场。我们可以假定速度场不随时间变化。当流动开始转变为湍流时,即使入口的流率不随时间变化,流动中也会出现混沌振荡,因此无法再假定流动不随时间变化。在这种情况下,需要求解瞬态 Navier-Stokes 方程,所用网格也应足够精细,才能解析流动中最小涡流的尺寸。
除了在靠近实体壁的粘性底层中,湍流耗散通常主导了各处的粘性耗散。在这里,湍流模型(例如低雷诺数模型)必须不断降低湍流水平。或者,必须使用壁函数来计算新的边界条件。
在旋转机械的模拟过程中通常我们会选择使用壁面函数来处理近壁面的流动。
壁面函数。
一般认为在近壁面的速度分布与对数分布接近,所以这就提供了一种在数值上计算离壁面一定距离内的流体的速度的函数的额方法。这样的函数就叫做壁面函数。
当引入壁面函数之后,就不再需要对近壁面内的流体进行数值求解,可以直接得到与近壁面相邻控制体的节点变量值。这也就不需要在网格划分时对近壁面的流域进行边界层网格划分。这样可以节省计算机的计算时间而且不需要过于精细的网格划分。而且在边界层中的层流底层中粘性力起主导作用,这也能够在湍流模型不考虑粘度的影响。因为壁面函数是一种经验函数,要想获得比较精确的数值解,就要选择合适的壁面函数。而且壁面函数不考虑粘性力的影响,所以在高粘性的流动中并不适用。同样的,壁面函数页不适用于低雷诺数流动或者近壁面效应、大的压力梯度导致的边界层分离。在CFX 软件中,提供了三种壁面函数,分别是标准壁面函数、增强壁面函数以及基于w方程的自动近壁面处理。






