本文摘要(由AI生成):
文章主要介绍了工业互联网中数字孪生系统的机理+数据融合建模方法,该方法可以充分发挥机理仿真可解释性和泛化能力强、数据驱动模型灵活性和可学习的优势,为未来数字孪生系统提供高效、灵活的工具和方法。文章首先阐述了数字孪生系统的基本架构,然后介绍了研究进展,包括模型选择、应用场景等。最后,文章指出了该方法面临的挑战,包括融合模型的精度、收敛性、可解释性和鲁棒性问题,以及构建可验证的标准数据集和开源社区等。
作者:李硕 刘天源 黄锋 解鑫 张金义
转自:信息通信技术与政策
李硕, 刘天源, 黄锋,解鑫,张金义. 工业互联网中数字孪生系统的机理+数据融合建模方法[J]. 信息通信技术与政策, 2022,48(10):52-61. 工业互联网的快速发展为学术界以及工业界带来了新型研发范式——数据密集型科学发现,融合物理机理以及数据驱动的建模方法是其中的研究热点之一,这种方式可以充分发挥机理仿真可解释性和泛化能力强、数据驱动模型灵活性和可学习的优势,为未来数字孪生系统提供高效、灵活的工具和方法。通过聚焦于工业互联网中构建数字孪生系统的机理+数据融合建模方法,首先阐述了基本数学原理以及建模方法,并对比了机理+数据融合建模与传统数据模型、机理模型的区别;然后从模型选择、物理机理约束以及实际任务需求3个角度详细给出了机理+数据融合建模方法的构造过程,总结了目前学术界的最新研究进展;最后介绍了国内外关于机理+数据融合建模方法在工业设备设计优化、生产制造、运行维护方面的实际落地应用场景。 关键词:深度学习;机理仿真;数据驱动;物理启发神经网络;数字孪生 中图分类号:TP393.09;TP241;F49
文献标志码:A 引用格式:李硕, 刘天源, 黄锋, 等. 工业互联网中数字孪生系统的机理+数据融合建模方法[J]. 信息通信技术与政策, 2022,48(10):52-61.
DOI:10.12267/j.issn.2096-5931.2022.10.008
随着近十年工业互联网技术的快速发展、分布式传感器和高性能计算设备的逐渐进步以及仿真建模算法的更新迭代,学术界和工业界积累了海量的多层级数据,从不同角度反映了工业生产过程中的内在物理信息[1],这为大数据的发展提供了良好的土壤,形成了数据驱动的新型范式,学者们[2]将之称为“第四范式”——数据密集型科学发现,以区别于实验归纳范式、模型推演范式和仿真模拟范式3种传统研究范式,强调直接从大量已知数据中自行归纳、推导和预测,获得未知且可信的结论。 近5年来,以深度学习[3]为代表的数据驱动方法不仅在视觉、自然语言处理以及博弈类场景应用中超越了人类,更在蛋白质结构预测[4]、三体问题[5]、气象预报[6]、核聚变控制[7]等一系列基础科学以及工业界难题中取得了重大突破。可以断言,人类社会正处于由仿真模拟范式向数据密集型科学范式的过渡发展阶段。 在工业互联网数据和深度学习算法的双重驱动下,“数字孪生系统”(Digital Twin)[8]在这个时代被赋予了更强大的生命力,这种技术体系可以有效结合目前过渡阶段的仿真模拟和数据驱动方法,充分挖掘服役历史、实时传感数据以及物理知识,用数字虚拟模型表征物理实体状态,实现对物理系统的理解、学习、推理和预测。经过近十年的技术储备和发展,数字孪生系统已经被认为是工业互联网中的战略性技术之一,是解决新时代工业产品全生命周期中设计、制造、服役和运维问题的有效方法。 构建数字虚拟模型是数字孪生系统技术的重中之重。与传统基于物理机理的模型不同,数字孪生系统更强调仿真的快速实时(快速反映物理世界的变化、计算响应速度快)和反馈学习(利用物理实体反馈的数据进行自我学习和完善),并且要求建模和仿真可以和更多的工业真实场景实现频繁的信息交互,以便实现模型的自动更新迭代;而机理仿真受制于求解速度,对计算机资源消耗巨大,难以布置到工业现场的边缘设备中,且无法对物理世界反馈的数据和经验进行再学习,必须借助人类对数据的理解进行调整;纯粹的数据驱动模型难以嵌入物理规律以及领域知识,而现阶段传感器测量仍然存在固有缺陷,这导致构建的模型缺乏可解释性,尤其是在处理非线性、多学科和多尺度的物理系统时,模型的精度低、稳定性差且泛化能力严重不足。 总之,就目前发展而言,无论是机理仿真还是数据驱动均难以满足未来工业互联网的发展需求。 其中,x表示对物理系统模型的输入变量(时间、空间坐标等);y表示需要获得的输出变量(物理场、信号等超高维变量);N[y]表示输出y对输入x的各阶微分、差分、积分或非线性算子构成的映射,这个方程由物理第一性原理在具体场景中给出,例如描述航天飞行器运动中的万有引力和牛顿力学定律、流体力学中的N-S方程(N-S:Navier-Stokes)、电磁场的麦克斯韦(Maxwell)方程、统计力学中的玻尔兹曼(Boltzmann)方程、量子力学中的薛定谔(Schrödinger)方程等;θ表示系统参数,用来表征系统的拓扑、几何以及物理特性。 一般而言,为了获得y和x的映射关系,需要求解上述方程组。例如,连续介质力学中在空间域上采用有限元方法、有限体积方法离散,时间域利用Runge-Kutta法离散,当然更加灵活的无网格离散方法近年来也是研究热点之一。虽然在过去半个世纪得益于计算硬件以及算法的进步,基于机理的建模-仿真-求解方法获得了长足的发展,被广泛应用于工业领域,大幅减少了不必要的试验、加快了设计研发周期并节省了实际运维成本;但目前仍然面临诸多挑战:前处理以及后处理过程极度繁琐、计算时间过长或计算资源消耗过大、难以适应灵活的任务需求(如信息缺失时的反向问题);甚至在近十年基于传统机理方法的发展已经裹足不前[9]。 数据驱动的方法避免了求解上述复杂的数学物理方程,通过将关注的物理场或信号y简化为低维信息,然后采用一个近似模型逼近上述方程的解,例如设计优化中常用的经验公式、代理模型以及对物理减缩模型,从而采用机器学习模型构造输入和输出之间的映射关系,通过最小化模型预测和标记数据之间的差异确定模型中的待定参数,具体如公式(2)所示。 其中,F(x;Θ)为构建的预测模型,Θ为模型中的待定参数,L(y^,y)衡量模型与标记数据之间的差异,在机器学习中也被称为损失函数,上述最小化损失函数的过程也称为训练过程;在经过大量标记数据完成训练后获得模型的最佳参数Θ∗,在实际使用时即可带入模型F(x;Θ)中进行快速预测,这种方式能够有效缓解实际使用机理仿真的计算量大/时间成本高的问题。虽然工业物联网目前可以为数据驱动方法提供大量的训练数据,但这些数据存在分散性、有限性、高噪声以及潜在同质化的缺陷(例如在故障检测中,大量故障工况运行数据是无法采集的,而且传感器的可测量位置极为有限且噪声成分极大);同时,目前这种完全数据驱动的方法缺乏对物理系统的建模,使得专业人员无法解释这些数据,更不能高效地利用这些数据,而获得模型的精度和可靠性也存疑。 机理+数据融合模型通过将物理机理嵌入数据驱动模型[10]中,可充分发挥机理模型可解释性和泛化能力强、数据驱动模型灵活和可学习的优势。从机器学习的视角来看,需要根据实际物理问题满足的对称性以及工业场景选择合适的机器学习模型,此外还需引入如下物理机理以及工业过程任务需求的损失函数。 其中,ym、y^m分别表示物理系统中的传感器采集获得的数据以及模型在对应测点预测的数据;N[y^](x;θ)表示将机器学习模型预测结果带入公式(1)获得的方程残差;‖N[y^](x;θ)‖表示残差范数;T(x,y^)表示实际任务需求中的目标函数;λN、λT表示训练时平衡各个损失的权重。
数字孪生系统中3种建模方法的关系如图1所示,机理+数据融合模型整合了两种传统建模方式,具体而言,相比于公式(2),公式(3)修正了所有输出的损失函数为稀疏布置传感器的可测量输出损失,还引入了物理机理约束的正则项以及任务需求的目标,以确保学习获得的模型可以满足物理方程和任务需求的约束。 图1 数字孪生系统中3种建模方法之间的联系以及区别
事实上,机理+数据融合建模方法的思想可以追溯到更早的物理学建模方法[11],例如传热学中的试验关联式和部件剩余寿命预测的经验公式都是基于这类思想——将复杂的物理系统通过经验知识简化为低自由度的系统,并抽象出简化过程中待定的参数,由于模型中包含了对物理系统的经验性反应,增强了模型的可解释性且减少了模型中的待定参数,推而广之,理论物理的重整化思想(如Boltzmann方程向N-S方程简化),工程的模型降维(如管道中忽略三维流动效应只研究沿管道流动方向的一维流动)本质都属于此类建模方法。相关抽象目前是由人工经验或领域知识给出的,而在机理+数据融合模型中,有望通过模型选择、物理约束以及任务需求将这个抽象过程通过机器学习或数据驱动方法表征出来,接下来本文主要从这3个方面讨论机理+数据融合建模方法的最新研究进展。 2.1 模型选择
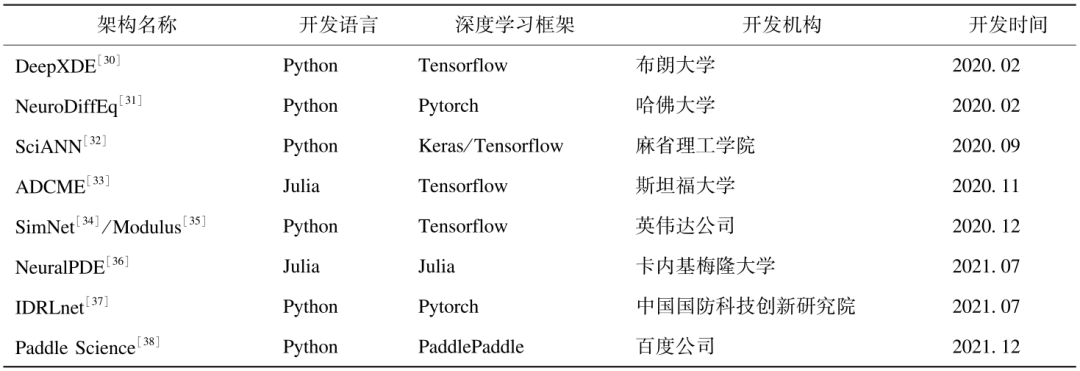
传统的代理模型(Surrogate Model)(如多项式、支持向量机、径向基模型、基于树的模型、高斯过程等方法)通过直接构造输入参数和输出的映射关系形成代理模型,由于模型简单且无需人工干预,被广泛应用于计算成本较高的黑箱函数的优化和控制任务中[12],但难以处理物理建模中所关注的物理场信息(一般可表示为在空间域和时间域上分布的高维张量)。过分简化的建模方式缺乏对物理系统本身的关注,依赖繁琐的特征工程以及大量数据采样,因此难以适用于精细化的物理系统建模。 减缩模型(Reduced Order Model)是通过数据驱动的方法或者经验分解的方法对原始的物理系统进行降阶或减缩,减少对高维信息描述的复杂度,继而加快对物理场或信号的求解和预测,常用的方法有本征正交分解和动态模态分解等方法。这些方法不仅展现出了良好的效果,同时也具备一定的可解释性;但也存在明显的缺陷,如处理复杂非线性问题依赖于核函数、基函数的选择,与问题不匹配时可能会导致模型表达能力不足或者训练收敛困难;此外,在将整个物理场或信号展开成一维向量时,未对定义在求解域的时空关联性以及物理量间的关联性建模,无法捕捉时间上的瞬态突变、空间上多尺度的信息,不具备物理约束中要求的空间平移、旋转不变性,限制了本身的应用范围[13]。 利用神经网络(Neural Network)作为近似映射对物理系统建模、求解可以追溯到20世纪90年代的若干工作[14-15]中,但受制于硬件效率以及算法的灵活性,一直以来没有被关注。 自2012年以来,深度神经网络的发展将机器学习方法带入了深度学习(Deep Learning)时代,相比于传统机器学习,深度学习具备更强的表达能力、更广泛的适应性、更显著的灵活性。 从计算机视觉和时序信号处理中发展出的各种神经网络算子,如卷积神经网络(Convolutional Neural Network,CNN)、关注时序信号的循环神经网络(Recurrent Neural Network,RNN)以及近年发展迅速的Transformer结构、图神经网络(Graph Neural Network,GNN)结构以及处理离散点云数据的点云网络等结构,可以灵活地处理工业互联网或机理仿真获得的超高维数据。例如,CNN可以有效地分析结构化数据[16];RNN适合对时间关联信息建模 [17];图神经网络可以适应非结构化网格数据[18];点云网络可以用于处理无网格的物理场[19];注意力机制可以处理多尺度物理信息[20];利用傅里叶算子分解[21]可以捕捉物理场的低频成分,提升模型对物理系统的表征性能。同时,这些方法保留了物理场在空间域、时间域以及拓扑内的不变性,通过这些物理对称性的约束可以显著减少模型的冗余度并增强可解释性,使得模型可以更加有效地处理超高维的物理系统。 在损失函数中引入物理系统方程的正则项约束,典型工作是物理信息神经网络(Physics-Informed Neural Network,PINN)[22],这种方法通过自动微分机制将物理系统遵循的动力学方程的微分形式纳入模型的损失函数中,使模型具备更强的物理解释性和对参数θ的泛化能力。PINN方法由于采用深度神经网络,充分利用深度学习中的自动微分机制,将物理约束通过损失函数引入神经网络,形成了端到端的微分方程求解器[23],补充了必要的边界条件或初始条件等,即可应用于各种偏微分方程和常微分方程的求解,如流体力学N-S方程[24]、弹塑性问题的静力学方程[25]、量子力学中的薛定谔方程[26]、分数阶微分方程[27]、气象问题的洛伦兹方程[28]、新冠病毒传播的动力学模型[29]。 PINN方法是目前机理+数据融合建模方法中发展的较为成熟的方向,在学术界引起了广泛的关注,且许多研究机构基于主流深度学习框架开发了相应的架构(见表1),目前除了美国以外,我国的国防科技创新研究院和百度公司也率先开发了相应的架构,尤其是百度公司目前基于国产化的深度学习框架PaddlePaddle开发的Paddle Science。 当然除了上述的自动微分方法引入物理约束,还有一些结合传统机理仿真模型的引入方式,例如利用有限差分、有限体积和有限元[39]格式构造。广义而言,谱方法、无网格方法也可以看作其中的一种,只是这两种方法选择了另外的可学习模型构造函数逼近器,再用加权余量法等数值求解方法计算损失函数。当然,从物理本质上讲选择合适的网络模型与物理规律的约束实际上是密不可分的,事实上近两年来PINN的重要发展方向正在朝统一两种方式到一个架构[10]中走,例如采用不同形式的网络模型[40]、与算子驱动方法结合[41]、与仿真模拟结合[39]、模型迁移[42]、更加高效的计算方式[43]、更加稳定的训练过程[44]、更加灵活的任务构造[45]。 机理+数据融合建模方法的最大优势是可以将虚拟模型本身与数字孪生系统中的设计、制造、控制、运维等任务需求灵活对接,并充分发掘海量传感器获得的数据,这是机理模型方法所不具备的。考虑公式(1)中更一般的问题,即方程中描述物理系统的部分参数θ需要被识别、控制或优化,在求解方程时是未知的,这导致方程一般是不适定的,在传统机理方法中需要大量的数值仿真对参数进行搜索,甚至结合数据驱动方法对参数进行寻优。而在机理+数据融合模型中,可以将该部分未知参数纳入模型中,即令θ∈Θ 显然此时原始方程增加了未知数,因此需要利用具体任务的约束将待求解问题封闭,从而转化为在机器学习方法中的可优化问题。实际工业场景中的任务可大致构造成如下3类方式。 (1)在物理场重构或系统的参数辨识问题中,由于缺失了部分边界条件、初始条件、几何信息、物理性质参数,必须引入必要的可测点使方程封闭,因此需在测点中补充更多的传感器测量,即 (2)在设计优化任务中,需要对部件的几何信息或工况参数进行优化,因此需要补充待优化目标,使得被设计对象获得更好的设计性能,即 (3)在控制问题中,需要保证系统的某个输出参数接近需要达到的控制目标,因此需要补充待控制目标,补充待控制目标和实际目标之间的差异,即 T(x,y^)=‖∫J(y^)dx-γ(x;θ)‖ (6) 其中,∫J(y^)dx表示需要优化或控制的目标,一般可表示为系统输出y的函数的积分形式(如机翼设计中的升力阻力比、换热结构的传热及阻力性能、承载结构的应力或载荷等);γ(x;θ)为控制目标;y^m、ym表示实际可布置测点的测量结果。 鉴于各种任务的一致性,在机理+数据融合模型中可以将这几种任务统一在一起[46],从而更加凸显机理+数据融合建模方法的灵活性和通用性,事实上实际工业场景中往往也需要同时兼顾上述3种任务。 近两年来,这种机理+数据融合建模方法已经被用于不同的物理场重构任务,如散热结构的设计[47]、基于核磁共振图像及少数测点的血管状态重构[48];系统参数辨识任务,如材料的几何缺陷检测[49]、汽车扭振阻尼结构的参数识别及校正[50];优化任务,如机翼形状优化[18]、电力系统优化[51];控制任务,如流动控制[45]、四容水箱液位控制[52]。另外,这种方法也能胜任一些复杂系统的物理场以及关注的性能参数预测,如热化学反应过程中的温度场预测[42]、气动轴承的气膜厚度以及力学特性预测[53]。 此外,虽然本文是以监督学习形式给出的物理机理嵌入方式,实际上该方法还可以与无监督学习方法以及强化学习方法结合,以进一步扩展该建模方式的应用场景,如进行物理系统的动力学方程的发现[54]、形状设计优化[55]、复杂的湍流控制[56]和电网系统控制[57]。 机理+数据融合模型由于其灵活性以及通用性,也获得了工业界的广泛关注。世界范围内的大型重工业企业开始陆续布局该模型,将这种方法应用于工业领域的设计优化—生产制造—运行维护环节,从而实现工业互联网中的数据闭环。例如,美国通用电气公司和安斯科技(ANSYS)公司、英国罗尔斯·罗伊斯(Rolls-Royce)公司、法国达索(Dassault)公司,德国西门子(Siemens)公司、我国百度公司等相继推出了利用机理+数据融合方法构建数字孪生系统的战略规划,并在实际工业场景中实现了落地应用。 在设计优化方面:美国通用电气公司[58]基于工业互联网技术与安斯科技公司合作打造了基于数值仿真的数字孪生系统,结合结构、热学、电磁、流体以及控制等多物理场耦合分析技术,构建了更加精确快速的综合仿真模型来分析、预测航空发动机的性能,通用电气公司于2018年宣称已经拥有120 万个数字孪生系统;英伟达(Nvidia)公司开发了Modulus[34]用于融合物理知识与数据以快速响应设计需求,为芯片散热的流场模拟提供了新的解决方案,使计算流体动力学等模拟的速度比传统工程模拟和设计优化工作流程方法加快1 万倍。 在生产制造方面:Fero Labs公司利用机器学习分析传感器数据,预防机器故障并减少资源浪费,每年为钢铁生产企业节省数百万美元的成本;安斯科技公司在材料分析中结合专家经验与机器学习方法,取得了比反复试验效果更好、改进更快、成本更低的结果;西门子利用深度学习使用天气和部件振动数据来不断微调风机,使转子叶片等设备能根据天气调整到最佳位置,从而提高了发电效率、增加了发电量。 在运行维护方面:英国罗尔斯·罗伊斯公司在最新的UltraFan航空发动机[59]的验证机中对每块风扇叶片都安装了传感器,并构造了数据孪生体,辅助叶片运行的健康管理;西门子利用数字孪生的混合建模模型[60]辅助电厂运维,使得燃气轮机的性能增加3.5 Mw,氮氧化物(NOx)排放量下降10%;法国电力集团利用融合建模方法的数字孪生系统进行设备故障诊断以及健康管理,故障检测准确率达到87%;百度公司[61]将机理模型、机器学习与环保水务业务深度融合,帮助水务公司实现节能降耗5%~15%,停机时间减少50%,总成本降低5%~10%,设备利用率提升5%~15%。 2021年8月,美国国防部[62]发布关于开展燃气轮机的大规模集成模拟和综合仿真的研究项目,相关研究人员认为:近期流体力学和人工智能方法的融合出现了巨大突破,有助于提升下一代燃气涡轮发动机的效率和安全性。同时,俄罗斯土星公司也报道了对船用重型燃气轮机的数字孪生项目,并声称目前已完成了第一阶段关于变速箱的融合建模,表示该方法将有助于减少下一代船用燃气轮机的设计时间和成本、缩短试验测试过程,提升产品生命周期的管理质量。由此可见,无论是在民用还是国防工业,机理+数据融合模型已经逐渐融入了新一代工业互联网的数字孪生系统。 综上所述,“第四范式”下的机理+数据融合建模方法是实现数字孪生系统中实时或准实时仿真、模型—数据双向反馈的理想工具,可以在统一的架构下灵活地处理工业领域不同的任务需求,这种方法 正在重塑着传统工业领域,引领着新一轮工业互联网技术的发展,也必将在未来扮演关键角色。但仍然需要承认的是:如何将工业中有限容量的数据和物理机理更加高效的结合,无论是将物理知识和经验嵌入机器学习模型,还是改造机理仿真方法以自适应数据,相关探索均缺乏理论支撑,也面临着新的挑战。首先,融合模型的精度、收敛性、可解释性和鲁棒性问题无论是在理论上还是应用中都是亟需解决的问题;其次,构建可验证的标准数据集以及相关开源社区,在传统工业领域仍然是极为困难的;最后,将仿真模拟、实验室中获得的融合模型向真实工业场景推广,确保模型的可迁移性和泛化能力也是一大挑战。
[1] BRUNTON S L, NOACK B R, KOUMOUTSAKOS P. Machine learning for fluid mechanics[J]. Annual Review of Fluid Mechanics, 2020,52(1):477-508. [2] HEY T, TANSLEY S, TOLLE K. The fourth paradigm: data-intensive scientific discovery[J]. Proceedings of the IEEE, 2011,99(8):1334-1337. [3] LeCun Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015,521(7553):436-444. [4] JUMPER J, EVANS R, PRITZEL A, et al. Highly accurate protein structure prediction with AlphaFold[J]. Nature, 2021,596(7873):583-589. [5] BREEN P G, FOLEY C N, BOEKHOLT T, et al. Newton versus the machine: solving the chaotic three-body problem using deep neural networks[J]. Monthly Notices of the Royal Astronomical Society, 2020,494(2):2465-2470. [6] RAVURI S, LENC K, WILLSON M, et al. Skilful precipitation nowcasting using deep generative models of radar[J]. Nature, 2021,597(7878):672-677. [7] DEGRAVE J, FELICI F, BUCHLI J, et al. Magnetic control of tokamak plasmas through deep reinforcement learning[J]. Nature, 2022,602(7897):414-419. [8] TAO F, CHENG J, QI Q, et al. Digital twin-driven product design, manufacturing and service with big data[J]. The International Journal of Advanced Manufacturing Technology, 2018,94(9-12):3563-3576. [9] RUNCHAL A K, RAO M M. CFD of the future: year 2025 and beyond[M]. 50 Years of CFD in Engineering Sciences. Singapore: Springer Singapore, 2020:779-795. [10] KARNIADAKIS G E, KEVREKIDIS I G, LU L, et al. Physics-informed machine learning[J]. Nature Reviews Physics, 2021,3(6):422-440. [11] KOCh-JANUSZ M, RINGEL Z. Mutual information, neural networks and the renormalization group[J]. Nature Physics, 2018,14(6):578-582. [12] IULIANO E. Application of surrogate-based global optimization to aerodynamic design[M]. Springer International Publishing, 2016. [13] KUTZ J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017,814:1-4. [14] THOMPSON M L, KRAMER M A. Modeling chemical processes using prior knowledge and neural networks[J]. AIChE Journal, 1994,40(8):1328-1340. [15] LAGARIS I E, LIKAS A, FOTIADIS D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998,9(5):987-1000. [16] LONG Z, LU Y, DONG B. PDE-Net 2.0: learning PDEs from data with a numeric-symbolic hybrid deep network[J]. Journal of Computational Physics, 2019,399:108925. [17] MOHAN A T, TRETIAK D, CHERTKOV M, et al. Spatio-temporal deep learning models of 3D turbulence with physics informed diagnostics[J]. Journal of Turbulence, 2020,21(9-10):484-524. [18] XU M, SONG S, SUN X, et al. A convolutional strategy on unstructured mesh for the adjoint vector modeling[J]. Physics of Fluids, 2021,33(3):036115. [19] KASHEFI A, REMPE D, GUIBAS L J. A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries[J]. Physics of Fluids, 2021,33(2):027104. [20] PENG W, YUAN Z, WANG J. Attention-Enhanced neural network models for turbulence simulation[J]. Physics of Fluids, 2022,34(2):025111. [21] LI Z, KOVACHKI N, AZIZZADENESHELI K, et al. Fourier neural operator for parametric partial differential equations[J]. arXiv Preprint, arXiv:2010.08895, 2020. [22] RAISSI M. Deep hidden physics models: deep learning of nonlinear partial differential equations[J]. arXiv Preprint, arXiv:1801.06637, 2018. [23] SUN L, GAO H, PAN S, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data[J]. Computer Methods in Applied Mechanics and Engineering, 2020,361:112732. [24] RAISSI M, YAZDANI A, KARNIADAKIS G E. Hidden fluid mechanics: learning velocity and pressurefields from flow visualizations[J]. Science, 2020,367(6481):1026-1030. [25] HAGHIGHAT E, RAISSI M, MOURE A, et al. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2021,379:113741. [26] PFAU D, SPENCER J S, MATTHEWS A, et al. Ab initio solution of the many-electron Schrdinger equation with deep neural networks[J]. Physical Review Research, 2020,2(3). [27] GULIAN M, RAISSI M, PERDIKARIS P, et al. Machine learning of space-fractional differential equations[J]. SIAM Journal on Scientific Computing, 2019,41(4):A2485-A2509. [28] RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Multistep neural networks for data-driven discovery of nonlinear dynamical systems[J]. arXiv Preprint, arXiv:1801.01236, 2018. [29] MALINZI J, GWEBU S, MOTSA S. Determining COVID-19 dynamics using physics informed neural networks[J]. Axioms, 2022,11(3):121. [30] LU L, MENG X, MAO Z, et al. DeepXDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021,63(1):208-228. DOI:10.1137/19M1274067. [31] CHEN F, SONDAK D, PROTOPAPAS P, et al. NeuroDiffEq: a Python package for solving differential equations with neural networks[J]. Journal of Open Source Software, 2020,5(46):1931. [32] HAGHIGHAT E, JUANES R. SciANN: a Keras/TensorFlow wrapper for scientific computations and physics-informed deep learning using artificial neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2021,373:113552. [33] XU K, DARVE E. ADCME: learning spatially-varying physical fields using deep neural networks[J]. arXiv Preprint, arXiv:2011.11955, 2020. [34] HENNIGH O, NARASIMHAN S, NABIAN M A, et al. NVIDIA SimNetTM: an AI-accelerated multi-physics simulation framework[J]. arXiv Preprint, arXiv:2012.07938, 2020. [35] NVIDIA Developer. NVIDIA modulus[EB/OL]. [2022-04-24]. https://developer.nvidia.com/modulus. [36] ZUBOV K, MCCarthy Z, MA Y, et al. NeuralPDE: automating physics-informed neural networks (PINNs)with error approximations[J]. arXiv Preprint, arXiv:2107.09443, 2021. [37] PENG W, ZHANG J, ZHOU W, et al. IDRLnet: a physics-informed neural network library[J]. arXiv Preprint, arXiv:2107.04320, 2021. [38] 飞桨PaddlePaddle——源于产业实践的开源深度学习平台. 深度学习常用数学知识[EB/OL]. [2022-04-24]. https://www.paddlepaddle.org.cn/tutorials/projectdetail/695184. [39] FANG Z. A high-efficient hybrid physics-informed neural networks based on convolutional neural network[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021:1-13. DOI: 10.1109/TNNLS.2021.3070878. [40] HY T S, TRIVEDI S, PAN H, et al. Predicting molecular properties with covariant compositional networks[J]. The Journal of Chemical Physics, 2018,148(24):241745. [41] LU L, JIN P, KARNIADAKIS G E. DeepONet: learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021,3(3):218-229. [42] NIAKI S A, HAGHIGHAT E, CAMPBELL T, et al. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture[J]. Computer Methods in Applied Mechanics and Engineering, 2021,384(3-4):113959. [43] MENG X, LI Z, ZHANG D, et al. PPINN: parareal physics-informed neural network for time-dependent PDEs[J]. Computer Methods in Applied Mechanics and Engineering, 2020,370:113250. [44] WANG S, YU X, PERDIKARIS P. When and why PINNs fail to train: a neural tangent kernel perspective[J]. arXiv Preprint, arXiv:2007.14527v1, 2020. [45] MOWLAVI S, NABI S. Optimal control of PDEs using physics-informed neural networks[J]. arXiv Preprint, arXiv:2111.09880, 2021. [46] BRUNTON S L. Machine Learning of Dynamics with Applications to Flow Control and Aerodynamic Optimization[C]. IUTAM Symposium on Critical Flow Dynamics Involving Moving/Deformable Structures with Design Applications,2021:327-335. [47] CAI S, WANG Z, CHRYSSOSTOMIDIS C, et al.Heat transfer prediction with unknown thermal boundary conditions using physics-informed neural networks[C]// ASME 2020 18th International Conference on Nanochannels, Microchannels, and Minichannels[C], 2020. [48] KISSAS G, YANG Y, HWUANG E, et al. Machine learning in cardiovascular flows modeling: predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2020,358:112623. [49] ZHANG E, DAO M, KARNIADAKIS G E, et al. Analyses of internal structures and defects in materials using physics-informed neural networks[J]. Science Advances, 2022,8(7):eabk0644. [50] YUCESAN Y A, VIANA F A C, MANIN L, et al. Adjusting a torsional vibration damper model with physics-informed neural networks[J]. Mechanical Systems and Signal Processing, 2021,154:107552. [51] MISYRIS G S, STIASNY J, CHATZIVASILEIADIS S. Capturing power system dynamics by physics-informedneural networks and optimization[J]. arXiv Preprint, arXiv:2103.17004, 2021. [52] ANTONELO E A, CAMPONOGARA E, SEMAN L O, et al. Physics-informed neural nets for control of dynamical systems[J]. arXiv Preprint, arXiv:2104. 02556, 2021. [53] LI L, LI Y, DU Q, et al. ReF-nets: physics-informed neural network for Reynolds equation of gas bearing[J]. Computer Methods in Applied Mechanics and Engineering, 2022,391:114524. [54] BAKARJI J, CHAMPION K, KUTZ J, et al. Discovering governing equations from partial measurements with deep delay autoencoders[J]. arXiv Preprint, arXiv:2201.05136, 2022. [55] CHEN W, FUGE M. BézierGAN: automatic generation of smooth curves from interpretable low-dimensional parameters[J]. arXiv Preprint, arXiv:1808.08871, 2018. [56] RABAULT J, REN F, ZHANG W, et al. Deep reinforcement learning in fluid mechanics: a promising method for both active flow control and shape optimization[J]. arXiv Preprint, arXiv:2001.02464, 2020. [57] YU L, HU W, ZHANG X, et al. Automatic generation control of ubiquitous power Internet of Things integrated energy system based on deep reinforcement learning[J]. Scientia Sinica Technologica, 2020,50(2):221-234. [58] Ansys. Ansys Collaborates with GE to Drive Digital Twin Value and Deliver the Promise of the Industrial Internet of Things[EB/OL]. (2016-11-16)[2022-05-19]. https://www.ansys.com/news-center/press-releases/11-16-16-ansys-collaborates-with-ge-to-drive-digital-twin-valve-iot. [59] Rolls-Royce. The sustainable solution for decades to come[EB/OL]. [2022-05-19]. https://www.rolls-royce.com/media/our-stories/innovation/2016/advance-and-ultrafan.aspx. [60] Siemens Energy. AI makes turbines young again[EB/OL]. [2022-04-25]. https://www.siemens-energy. com/global/en/news/magazine/2020/power-station-with-real-time-rejuvenation.html. [61] 天互数据. 百度智能云智能制造解决方案,开启中国制造的2025[EB/OL]. (2021-08-10)[2022-04-25]. https://www.idcs.cn/a/v2730. [62] The Defense Post. US DoD to work on project for digital copy of gas turbines[EB/OL]. (2021-08-26)[2022-04-25]. https://www.thedefensepost.com/2021/08/26/us-dod-digital-copy-gas-turbines/. Mechanism + data fusion modeling method in digital twin system for industrial internet LI Shuo, LIU Tianyuan, HUANG Feng, XIE Xin, ZHANG Jinyi (Baidu Online Network Technology Co., Ltd., Beijing 100086, China) Abstract: The development and prosperity of the Industrial Internet have brought a novel paradigm to the academic and industrial communities-Data-intensive Scientific Discovery. The modeling method of fusion physics mechanism and data driven is one of the research hotspots,which can provide efficient and flexible analysis tools for future digital twin system. This approach can benefit from both mechanism simulation (interpretability and generalization ability) and data-driven model (flexibility and learning ability), especially in the deep learning architecture. In this context, this paper focuses on the mechanism + data fusion method in the digital twin system for Industrial Internet. Firstly, the basic mathematical principles and modeling methods are established, while the differences between mechanism + data fusion modeling and traditional models are compared. Then, machine-learning model selection, physics mechanism constraints, and actual task requirements are introduced in detail, and the recent research progress and development are summarized. Finally, the actual application scenarios of this method are reported from three perspectives, including design optimization, manufacturing, and operation maintenance. Keywords: deep learning; mechanism simulation; data driven; physics-informed neural network; digital twin