CFD|桥梁二维数值风洞分析
三分力系数是桥梁抗风分析的必备参数,是抖振,驰振以及稳定性分析研究中的重要参数.三分力系数的取值直接影响桥梁抗风分析的精度,因此比较精确地计算桥梁断面三分力系数有着重要的意义。
CFD数值分析


箱式梁桥有无声屏障风系数评价
郑胜焕1 李英基2
摘 要
在这项研究中,执行计算流体分析(CFD) 来估计受风影响的箱式混凝土梁桥的风力系数。计算了无声屏障桥段的阻力系数、升力系数和扭转力矩系数,并将这些风力系数值与不同高度的声屏障桥段的风力系数值进行了比较。在计算流体分析中计算风功率系数时,应用剪切应力传递(SST)k-ω湍流模型,研究了摩擦阻力系数对总阻力系数的贡献。研究结果表明,当风向水平吹来时,阻力系数随着声屏障高度的增加而增加,而当桥段没有声屏障时,摩擦阻力的贡献最大。因此在桥梁设计中估算风力时需要考虑声屏障高度的影响,而墙体摩擦力在估算作用在桥梁上的风力时起到了重要作用。
关键词:隔音墙,箱桥,计算流体分析,风力系数,摩擦阻力系数
Evaluation of Wind ForceCoefficients of a Box-Type Girder Bridgewith Noise Barriers
ABSTRACT
In the study, computational fluiddynamics analysis was performed to estimate wind force coefficients for abox-type concrete girder bridge under the influence of wind. The drag, lift andpitching moment coefficients were obtained for the bridge section without noisebarrier and compared with those of the bridge section with noise barriers ofvarious heights. The shear stress transport k-ω turbulence model was employedto estimate the wind force coefficients, and the contribution of the frictiondrag force to the total drag force was investigated. It was found from thestudy that the drag force coefficients increased as the height of noise barrierincreased when a wind blew horizontally, and that the contribution of thefriction drag force was highest for the bridge section without noise barrier.It is concluded that the impact of the height of noise barriers should beconsidered in the design of bridges, and the friction force played an importantrole in evaluating wind forces on bridges.
Key words : Noise barrier, Box-typebridge, Computational fluid dynamics, Wind force coefficients, Friction dragforce coefficients
1 研究背景与目的
近来,多条高速公路建成,多座桥梁同时在建或加固。如果在这些高速道路上安装的桥梁附近有公寓和办公室等建筑物,交通噪声可能会对人员造成伤害。因此,在搭建桥梁结构的同时,也安装了隔音墙。但是,当强风或台风等强风吹到有隔音墙的桥梁上时,承受风压的风压面积会增加,因此在桥梁设计中需要考虑这种风压的增加.
执行风洞测试或计算流体动力学分析 (CFD) 以估计风作用在土木结构上所产生的风力。风洞试验大致可分为风功率试验和风压试验,风洞试验的缺点是难以利用风功率试验结果进行截面的详细设计。在风压试验中,只能测量垂直作用于结构表面的压力,而不能测量平行于结构表面作用的墙体剪力。计算流体分析(CFD)不仅可以计算垂直作用于结构表面的压力,还可以计算平行于结构表面作用的壁面剪力。目前,韩国桥梁与结构工程师学会(2015)提出了估算桥梁设计风压的标准。 Fransos 和 Bruno (2010) 通过计算流体分析 (CFD) 研究了梯形桥面的空气动力学行为,并计算了桥面边缘形状变化时的风力系数。Sarwar 等人 (2008) 通过使用 LES 湍流模型的三维计算流体分析估计了作用在箱形梁桥上的风力。Han et al. (2016) 通过计算流体分析计算了三种桥段的阻力系数,并根据雷诺数和有无防护围栏计算阻力系数。Mannini et al. (2010) 使用 URANS 方程(一种湍流模型)分析了各种雷诺数的二维矩形横截面周围的流动现象,然后将它们与风洞实验的结果进行了比较。Miranda et al. (2015) ) 计算在流体分析中使用 RANS 和 LES 湍流模型,研究了在大跨度桥梁中经常使用的双箱桥桥面周围的流动。他们发现,随着甲板间距的增加,两个甲板之间发生了强烈的动态相互作用,并将这一结果与实验数据进行了比较。
在这项研究中,我们通过计算流体分析 (CFD) 研究了在桥段、桥段左右两侧以及声屏障没有声屏障时,风力如何随声屏障高度变化接近中位数。此外,利用剪应力传递k-ω湍流模型,可以准确估计结构表面的壁面剪力(摩擦力),计算桥段风功率系数,以及壁面剪力的影响。

对于BOX型混凝土梁桥的计算流体分析,应设置桥梁结构周围的流动区域,确定流动区域的边界条件。如图。图 2 显示了用于计算流体分析的BOX 型混凝土梁桥周围的流动区域。从梁桥模型的剪切中心到流动区域的入口、出口和顶部的长度设置得足够宽,分别为梁桥模型长度 (L) 的约6.3、13.7和5倍。还有图图 2 显示了使用 CFD 分析程序 MIDAS NFX 输入的边界条件。共设置5个边界条件:入口端、出口端、上部外风、下部外风和结构墙体。入口端输入风速设置为 7.5 m/sec,出口端压力设置为 0。在上下室外空气的边界条件下,垂直方向(y方向)的流速设为0。结构的壁面设置为无量纲壁面距离条件(第一个节点的x方向流速为0)。图 3 显示了为 BOX 型混凝土梁桥的计算流体分析创建的单元。BOX型混凝土梁桥风压分布及周围流速进行了计算流体分析。图 1 显示了用于计算流体分析的箱式混凝土梁桥模型。对箱式混凝土梁桥无隔音墙(H=0)和梁桥有隔音墙高度为H的情况进行计算流体分析。梁桥有隔音墙的情况下,4种类型不同高度的隔音墙这被认为是。这四种声屏障的高度分别为H = 0.013 m、0.031 m、0.05 m和0.069 m,声屏障的实际尺寸分别对应Hp = 1 m、2.5 m、4.0 m和5.5 m。
对于BOX型混凝土梁桥的计算流体分析,应设置桥梁结构周围的流动区域,确定流动区域的边界条件。图 2 显示了用于计算流体分析的BOX 型混凝土梁桥周围的流动区域。从梁桥模型的剪切中心到流动区域的入口、出口和顶部的长度设置得足够宽,分别为梁桥模型长度 (L) 的约 6.3、13.7 和 5 倍。还有图图 2 显示了使用 CFD 分析程序 MIDAS NFX 输入的边界条件。共设置5个边界条件:入口端、出口端、上部外风、下部外风和结构墙体。入口端输入风速设置为 7.5 m/sec,出口端压力设置为 0。在上下室外空气的边界条件下,垂直方向(y方向)的流速设为0。结构的壁面设置为无量纲壁面距离条件(第一个节点的x方向流速为0)。图 3 显示了为 BOX 型混凝土梁桥的计算流体分析创建的单元。BOX型混凝土梁桥风压分布及周围流速。
通过有限元法分析分布,并使用 CFD 分析程序 MIDAS NFX。为分析创建了三角形和四边形网格。分析中使用的元素数量约为 233,000。对于每个分析案例进行10,000次迭代,每个分析案例的分析时间约为4小时。在本研究中,计算流体分析模型的结果是,k-采用ω(Shear Stress Transport)湍流模型,可以很好地表示结构周围的边界层流动,可以很好地估计作用在结构表面的剪应力。表示流动现象的 Navier-Stokes 方程 (Myeong Hyeon Gook, 2012) 是湍流模型的基础,定义如下:

如图4所示,风向阻力为FD,风向升力为FL, 显示了扭矩 MT 的方向。x方向为顺风,y方向为横风。另外,定义了表示风向的a的方向。顺时针方向定义为基于图中所示水平线的正(+) 风向。

3 结果与讨论
3.1 风速和风压分布
图 5 给出了计算流体分析得到的箱形梁桥截面周围的风速分布和风压分布。风速和风压分布是风向时隔音墙高度H=0.05m(实际高度Hp=4.0m)。图5(a)中的风速分布可以看出,在迎风侧的隔音墙高度中间出现了一个停滞点,在隔音墙的上部风速增大墙和梁的下部。图5(b)中的风压分布可以看出,在迎风侧的隔音墙中产生强正(+)压力,而在道路上部产生负(-)压力在隔音墙和隔音墙之间。

(a) 风速分布

(b) 风压分布
图 5. CFD 分析得出的箱型梁桥周围的风速和风压分布
3.2 与风洞试验结果对比
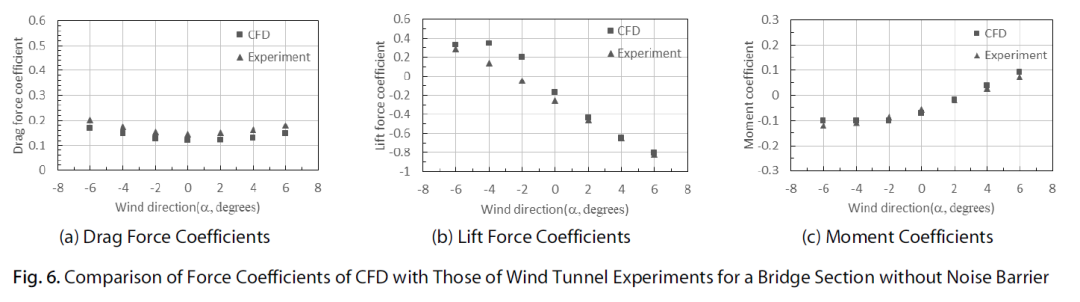
图 6 比较了在没有声屏障的情况下通过计算流体分析获得的每个风向的阻力系数 (CD)、升力系数 (CL) 和扭转力矩系数 (CM) 与风洞试验的结果。风洞试验在大宇建设技术研究所(2017)在同一模型上进行。如图。从图 6 可以看出,计算流体分析得到的风系数与风洞试验得到的结果非常相似。计算流体分析结果与风洞试验结果之间的阻力系数考虑的总风向平均差异约为 0.03,除升力的 -2 度和 -4 度外,总风向的差异约为0.03的平均系数,和的情况下,所有风向的平均扭矩约为 0.005。审查大宇建设技术研究所(2017)风洞试验报告后,桥梁截面的防护墙形状和中间断面的防护墙形状均制作为矩形,与实际形状相比被简化了。只要解释结果有差异,就被认为是原因。
3.3 风向系数
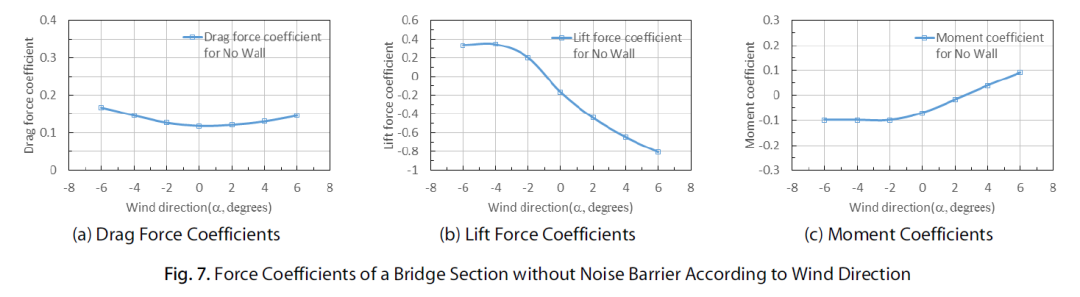
图 7 和表 1 至表 3 给出了桥段无声屏障时风向的阻力系数、升力系数和扭转力矩系数。图 7(a) 显示了根据风向的阻力系数 (CD)。当风向 =0 时,阻力系数为 0.118,以通过 =0 的直线为对称轴,风向正向或负向增加阻力系数对称增加。随着风向从=6增加到=-2,阻力系数从0.121增加到0.146;随着风向从负向=-2增加到=-6,阻力系数从0.126增加到 0.168。当负风向作用时,迎风面的迎风面积增加,因此阻力系数增加。从=-2,阻力系数从0.121增加到0.146;从=-2到=-6,阻力系数从0.126增加到0.168,向负方向增加。当负风向作用时,迎风面的迎风面积增加,因此阻力系数增加。
图7(b) 显示了在没有声屏障时根据风向的升力系数 (CL)。当风向=-2、-4、-6时,即负风向作用时,升力系数均呈正值,是向上拉起大梁的力。但是,当风向=0、2、4时,升力系数呈负值,负升力是指在风的作用下将桥板和大梁向下推向地面的力。尤其可以看出,当风向=6时,升力系数CL=-0.808呈现出较高的值。
图 7(c) 显示了在没有声屏障时根据风向的扭转力矩系数 (CM)。如果没有音障,可以看出扭转力矩系数小于阻力系数和升力系数,当=0、2、负风向时,扭转力矩系数在-0.018范围内为负为-0.1.值(顺时针),但当= 4和6时,正(+)值(逆时针)分别表示为0.038和0.091。



在图8和表1至表3中,在桥梁横断面的挡墙两侧安装高度H=0.05m(实际Hp=4.0m)的隔音墙,高度H=0.031 m(实际Hp=2.5m)安装在中间截面上,表示安装音障时根据风向的阻力系数、升力系数和扭转力矩系数。图8(a)显示了根据风向的阻力系数(CD)。风向=0时的阻力系数为0.215,比无声屏障时的阻力系数增加约82%(见表4)。当安装H=0.05m(实际Hp=4.0m)的声屏障时,阻力系数从0.200到0.290是平缓的,随着风向减小=2,直到风向=0、-6。
在图8和表1至表3中,在桥梁横断面的挡墙两侧安装高度H=0.05m(实际Hp=4.0m)的隔音墙,高度H=0.031 m(实际Hp=2.5m)安装在中间截面上,表示安装音障时根据风向的阻力系数、升力系数和扭转力矩系数。如图。图8(a)显示了根据风向的阻力系数(CD)。风向=0时的阻力系数为0.215,比无声屏障时的阻力系数增加约82%(见表4)。当安装H=0.05m(实际Hp=4.0m)的声屏障时,随着风向减小=2,阻力系数从0.200逐渐增加到0.290,直到风向、=0、-6。当风向改变为 =4,6 时,阻力系数从 0.205 迅速增加到 0.501。如表 4 所示,当风向 =-2、-4、-6 时,风阻系数与无声屏障情况相比分别增加了 88%、80% 和 73%,当风方向=2, 4, 6 阻力系数比没有声屏障的情况分别增加了66%、58%和242%。
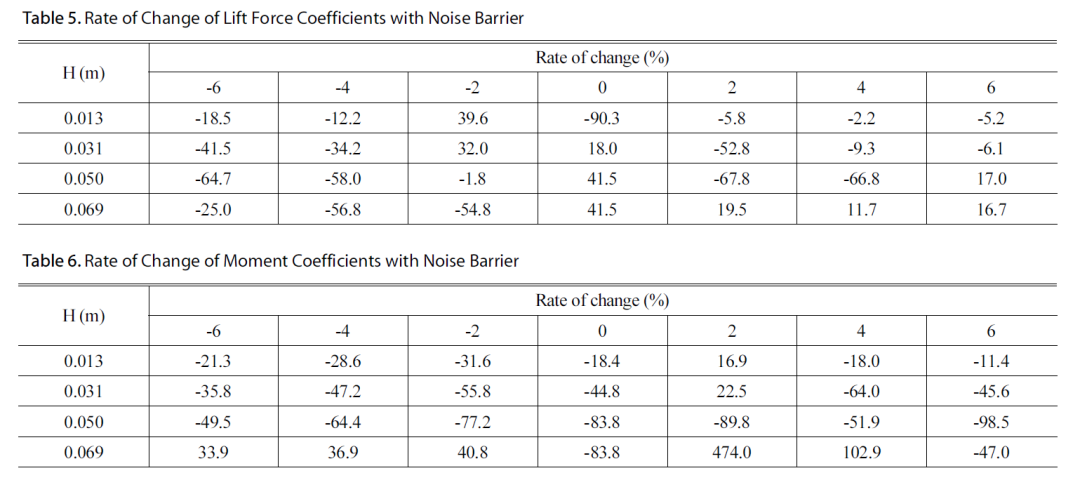
图8(b)显示了安装H=0.05m(实际Hp=4.0m)的声屏障时的风向升力系数(CL)。随着风向下降2度,直到风向 =0,-6,升力系数从 0.236 缓慢下降到 0.118,表明压力向上。在风向=2时,升力系数为0.142,即静压,当风向变为=4,6时,阻力系数从-0.214急剧增加到-0.945。如表5所示, H =0.05m(实际Hp=4.0m) 安装音障时,升力系数的绝对量级较不安装音障时降低2~68%, =0,6时除外。
图8(c)显示了安装H=0.05m(实际Hp=4.0m)的声屏障时的风向扭矩系数(CM)。与没有音障时类似,可以看出扭转力矩系数小于阻力系数和升力系数,并且当=0、6和负风向时,扭转力矩系数在该范围内为负从 -0.001 到 -0.050。显示负 (-) 值(顺时针),但当 =2、4 时,分别显示从 0.002 到 0.018 的正 (+) 值(逆时针)。此外,如表 6 所示,与没有声屏障的情况相比,扭转力矩系数的绝对量级降低了 49~99%。
3.4 声屏障高度的风系数
图9显示了风向=0时根据音障高度的阻力系数。无声屏障时,阻力系数(CD)为0.118,随着声屏障高度的增加,阻力系数增大。当声屏障高度H=0.05 m时,阻力系数取值为0.215。
对于风向= 0的声屏障高度的升力系数,当没有声屏障或声屏障高度低为H = 0.013 m时,升力系数(CL)为负(-)显示。当隔音墙高度大于H=0.013m时,升力系数呈正压,随着隔音墙高度的增加,升力系数也随之增加。当声屏障高度H=0.05 m时,升力系数值为0.236。
对于风向= 0 时根据音障高度的扭转力矩系数,在没有音障和没有音障的情况下,扭转力矩系数(CM) 的值(顺时针)均为负值(-)。音障的存在。无声屏障时,出现最大负(-)扭矩系数CM=-0.071,且随着声屏障高度的增加。
3.5 壁面剪力对整体阻力系数的贡献
前一章计算流体分析(CFD)计算的阻力系数、升力系数和扭转力矩系数是考虑平行于桥面作用的墙体剪力(摩擦力)计算得出的。如果在计算这些系数时不考虑墙体剪力,结果值就会不同,也就无法准确估算作用在桥梁上的风力。因此,在本研究中,计算了壁面剪力对风力系数(阻力系数和升力系数)的贡献,以了解壁面剪力(摩擦力)对风力系数计算的贡献程度。壁面剪力(摩擦力)对阻力系数的贡献由下式计算。
摩擦阻力系数的贡献=壁面剪切摩擦阻力系数/总阻力系数

该摩擦阻力系数的贡献是壁面剪切(摩擦)阻力系数与总阻力系数的比值。图 10 显示了摩擦阻力系数的贡献如何随着风向的变化而变化。如果没有音障,风向=-6~6时摩擦阻力系数的贡献约为25%~76%。特别是在=0和正风向=2、4、6时,摩擦阻力系数的贡献很大。当声屏障高度H=0.013m时,风向=-6~6时摩擦阻力系数的贡献率约为18%~43%。当音障高度H=0.031m时,风向=-6—6时摩擦阻力系数的贡献约为10%~33%。当声屏障高度H=0.05 m时,摩擦阻力系数对所有风向的贡献为16%~41%。当声屏障的高度最高时,H = 0.069 m,发现摩擦阻力系数对所有风向的贡献约为 22% 至 50%。研究结果表明,当没有声屏障时,摩擦阻力系数对总阻力系数的贡献最高。贡献高的风向为=-6~6,正风向=2、4、6。
图 11 显示了摩擦升力系数的贡献如何随着风向的变化而变化。在没有声屏障的情况下,摩擦升力系数的贡献非常小,风向=0,2 时分别约为 3.5% 和 0.1%。对于除这两个风向之外的其余五个风向,摩擦升力系数的贡献为-1.1%至-2.8%。当声屏障高度为 H = 0.013 m 时,摩擦升力系数对除风向= 0 外的所有风向的贡献为 -5.8% 至 1.9%。当声屏障高度H=0.031 m时,摩擦升力系数对所有风向的贡献为-5.6%~2.6%。当声屏障高度H=0.05m时,风向=-4、4、6时摩擦升力系数的贡献分别约为0.2%、6.7%和13.3%。摩擦升力系数对这三个风向以外的风向的贡献起到了将总升力系数从-1.2%降低到-12.4%的作用。当声屏障高度最高时,H=0.069 m,摩擦升力系数对所有风向的贡献为-14.4%~28%。研究结果表明,除少数风向外,摩擦升力系数对总升力系数的贡献相对较低。
4 结论
在本研究中,通过计算流体计算了纵横比为 0.15 的 BOX 型混凝土梁桥横截面的风产生的风系数,即桥梁横截面的高度与长度之比。分析(CFD)。风向为水平时(=0),无声屏障时阻力系数为0.118,随着声屏障高度(H)从0.013 m增加到0.05 m,阻力系数从0.142增加到0.215。升力系数在无声屏障或低声屏障时为负值,但随着声屏障高度的增加,升力系数为正值。无声屏障时升力系数为-0.167,声屏障0.05 m时升力系数为0.236。无声屏障时扭矩为-0.071,声屏障0.05 m时为-0.011,随着声屏障高度的增加而减小。研究结果表明,声屏障高度的变化对阻力系数的变化影响最大,因此在计算风速时需要考虑声屏障高度的影响。桥梁设计。此外,在本研究中,摩擦阻力系数的贡献是随着风向的变化而计算的。无声屏障时摩擦阻力系数对总阻力系数的贡献最大,此时摩擦阻力系数的贡献在25%~76%之间。除少数风向外,摩擦升力系数对总升力系数的贡献普遍较低,因此在计算作用在桥梁上的风力时,必须考虑壁面剪力(摩擦力),计算流体分析将这种摩擦力考虑在内。这将是一个很好的工具。
鸣谢
该项研究是在大宇建设的支持下进行的,我们在此表示感谢。
参考文献
Fransos, D. and Bruno, L. (2010). “Edgedegree-of-sharpness and free-stream turbulencescale effects on the aerodynamics of a bridgedeck.” Journal Wind Eng. Ind. Aerodyn.,Vol. 98, pp.661-671.
Han, Y., Chen, H., Cai, C. S., Xu, G., Shen, L. and Hu,P. (2016).“Numerical analysis on the difference of drag force coefficientsof bridge deck sections between the global force andpressure distribution methods.” JournalWind Eng. Ind. Aerodyn., Vol.159, pp. 65-79.
Korea Institute of Bridge and StructuralEngineers·Bridge Design Core Technology ResearchGroup (2015). Highway Bridge Design Code(LimitState Design) and Commentary (in Korean).
Mannini, C., Soda, A. and Schewe, G. (2010). “UnsteadyRANS modelling of flow past a rectangularcylinder: Investigation of Reynolds numbereffects.” Computers and Fluids,Vol. 39, No. 9,pp. 1609-1624.
MIDAS NFX (2017). CFDUser’s Manual, MIDAS.Miranda, S., Patruno, L.,Ricci, M. and Ubertini, F. (2015). “Numericalstudy of a twin box bridge deckwith increasing gap ratio by using RANS and LES approaches.” EngineeringStructures, Vol. 99,No. 15, pp. 546-558.
Myeong, H. G. (2012). CFD,Munundang (in Korean).Sarwar, M. W., Ishihara, T., Shimada, K., Yamasaki, Y.and Ikeda,T. (2008). “Prediction of aerodynamic characteristics of a boxgirderbridge section using the LES turbulence model.” Journal Wind Eng. Ind. Aerodyn.,Vol. 96, pp. 1895-1911.