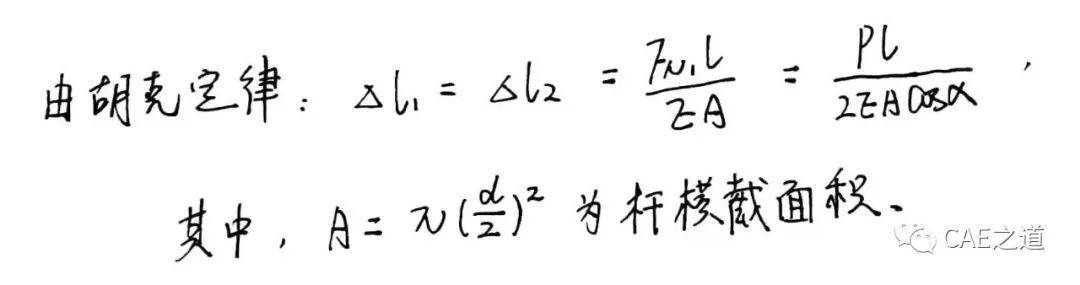ANSYS与材料力学之轴向拉伸和压缩(四)
本来笔者打算这次讲解应力奇异,奈何计算数据目前没在手里,因此先写了这篇文章,让大家在假期解解闷儿。
上篇文章,我们主要学习了拉压杆任意斜截面上的应力,并在使用ANSYS进行验证的同时,学习了提取任意截面上的应力结果的方法。今天我们一起来学习第四节——拉(压)杆的变形·胡克定律。
我们知道,胡克定律是力学弹性理论中的一条基本定律,它描述了固体材料受力以后,材料中的应力应变关系。下式为胡克定律的一种表达形式:
式中,E称为弹性模量(Elastic Modulus),是材料的一项重要弹性参数,数值因材料而异,表征材料抵抗弹性变形的能力。英国科学家Thomas Young曾研究了杆的弹性性能,所以之后弹性模量有时也称为杨氏模量(Young's Modulus),在ANSYS中的材料属性中,也是以Young's Modulus命名。
除弹性模量外,材料还有一个非常重要的弹性参数——泊松比(Poisson's ratio)。泊松比又称横向变形系数,常用字母ν表示。它定义为:在材料的比例极限内,横向线应变与纵向线应变的绝对值的比值。泊松比由法国科学家泊松(Simon Denis Poisson,1781-1840) 最先发现并提出。
此外,材料还有两项弹性参数:体积模量(Bulk modulus)和切变模量(Shear modulus)。其中,体积模量K=E/3(1-2ν)(这也是泊松比ν不能大于0.5的原因),切变模量G=E/2(1+ν),均可以用杨氏模量E和泊松比ν表示,所以我们把杨氏模量E和泊松比ν定为弹性材料的基本参数。如果做线弹性静力学分析,且不考虑重力作用的话,定义了这两个参数,就基本可以进行计算了。下图为WB中定义的线弹性材料,我们输入杨氏模量和泊松比之后,体积模量和切变模量会自动计算出来。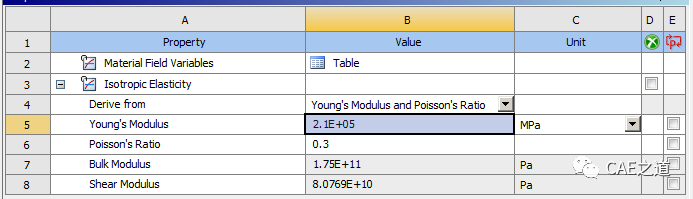
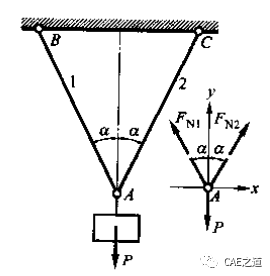
今天,我们将通过例题2-5,来研究该题的材料力学解法和ANSYS解法。
材料力学解法:
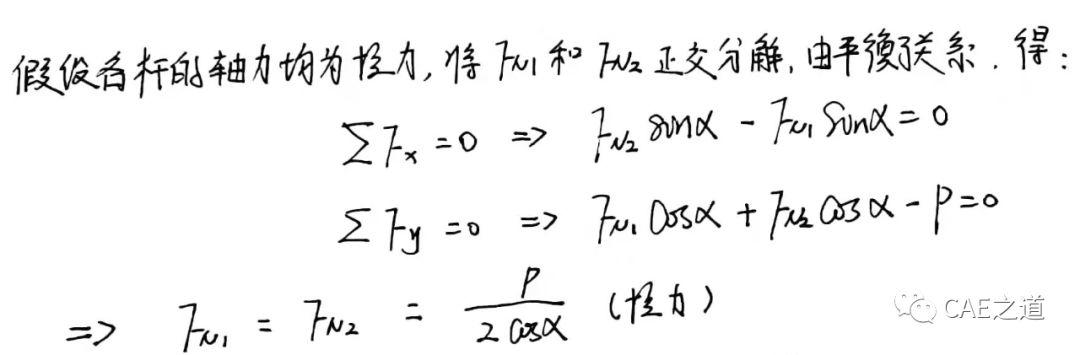
Step2:计算变形
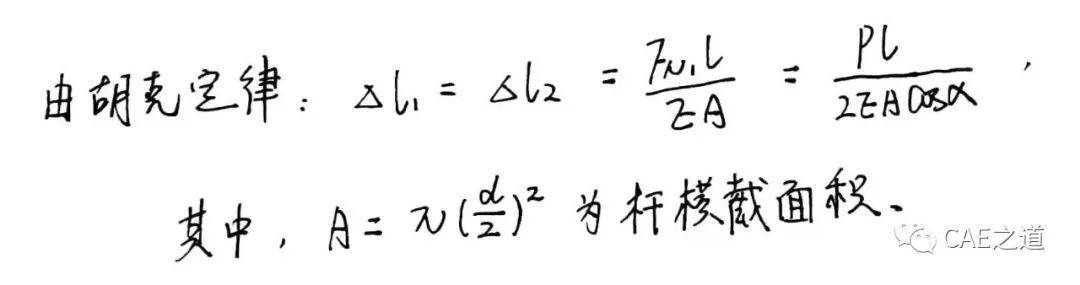
Step3:计算结点A的位移
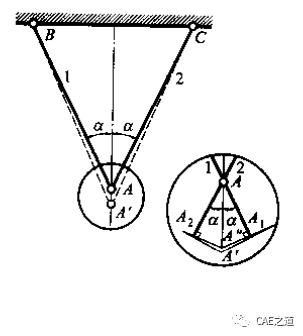
计算结点A的位移,需要用到小变形假设。首先我们假想将两杆在A点处拆开,并沿轴线分别增加△L1和△L2。但实际上变形后的两根杆还是铰接在一起的,满足几何相容条件。如下图,以B、C为圆心,以两杆伸长后的长度BA1、CA2为半径作圆弧,其交点A''即为A点的新位置。AA''为A点的位移。由于变形微小,故可过A1、A2分别作1、2两杆的垂线以代替圆弧,两垂线交于A',略去高阶微量,可认为AA'=AA''。由于杆系的对称性,故A'与A必在同一铅垂线上。

打开WB,将Static Structural模块拖入Project Schematic,并将其重命名为例题2-5。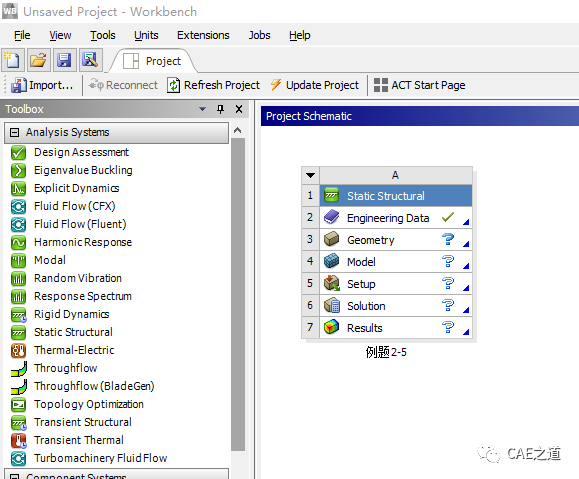
例题中给定了材料的弹性模量为E=210GPa,我们需要在Engineering Data中添加弹性模量为E=210GPa的材料,否则计算时软件会按照默认的Structural Steel材料计算。①双击A2 Engineering Data进入材料管理模块,点击Click here to add a new material,输入例题2-5,建立一个名为“例题2-5”的新材料。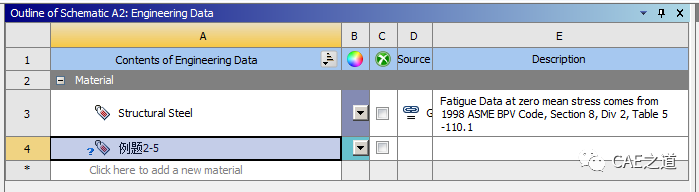
②单击新建的例题2-5材料,在左边的Toolbox中选择Linear Elastic,双击Isotropic Elasticity,表示创建一个各向同性的线弹性材料。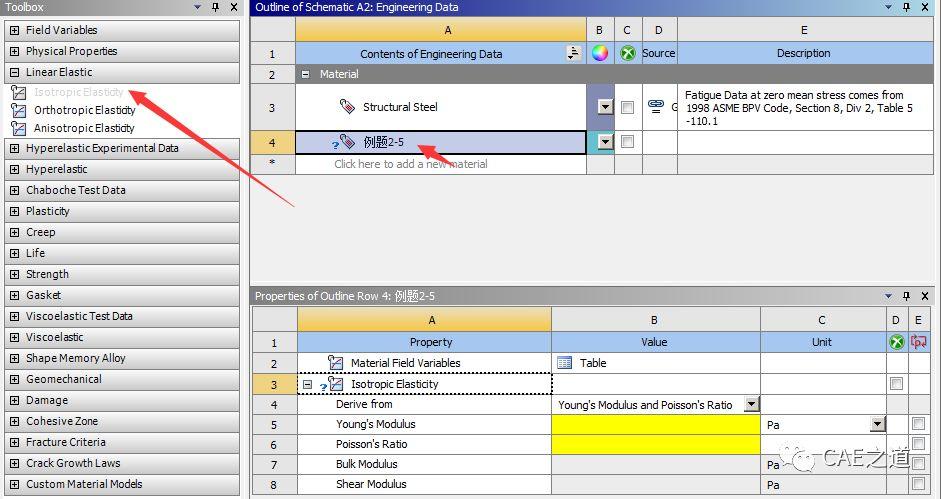
③在Properties of outline row 4:例题2-5中,将Isotropic Elasticity中的derive from设置为Young's Modulus and Poisson's ratio,即表示我们想要通过杨氏模量和泊松比来定义该材料。输入相应的值,此处我们将泊松比设置为0.3。我们发现,输入了杨氏模量和泊松比以后,切变模量和体积模量软件已自动定义。至此材料定义完毕,退出Engineering Data。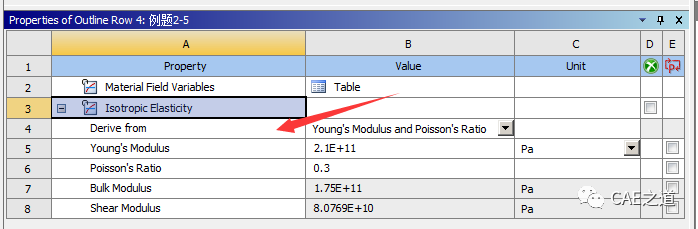
双击A3 Geometry进入SCDM,进行几何建模。①草绘几何:根据例题给定的尺寸,在xy平面内草绘出两条线。建模的方式很多,笔者选择将铰接点定为整体坐标系原点。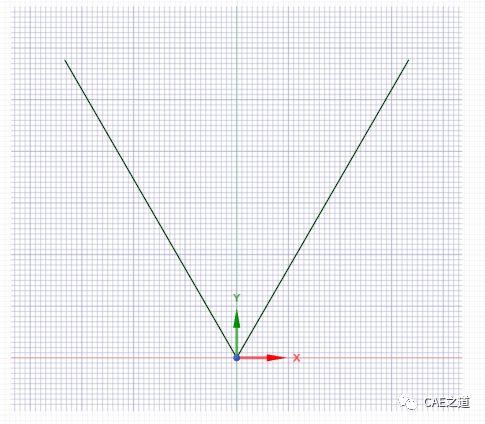
②建立杆截面:根据例题,该杆为直径25mm的圆截面杆。我们点击prepare→Profiles→circle,先创建一个圆截面(下图一)。然后在结构树中右键circle→Edit Bbeam Profile(下图二),将半径R改为12.5mm(下图三)。然后退出截面修改。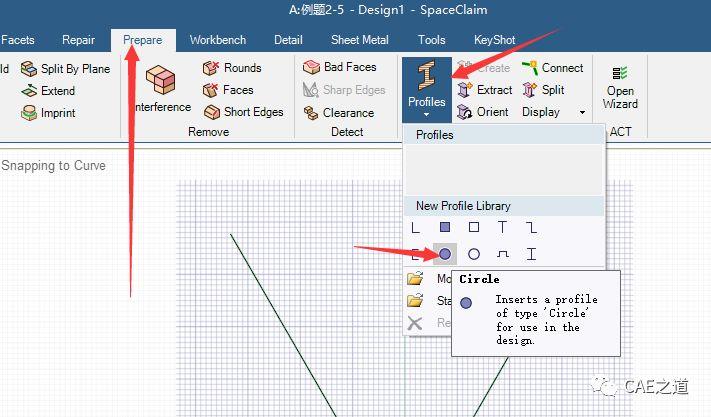
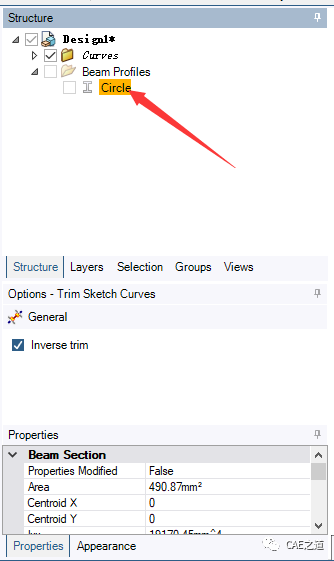
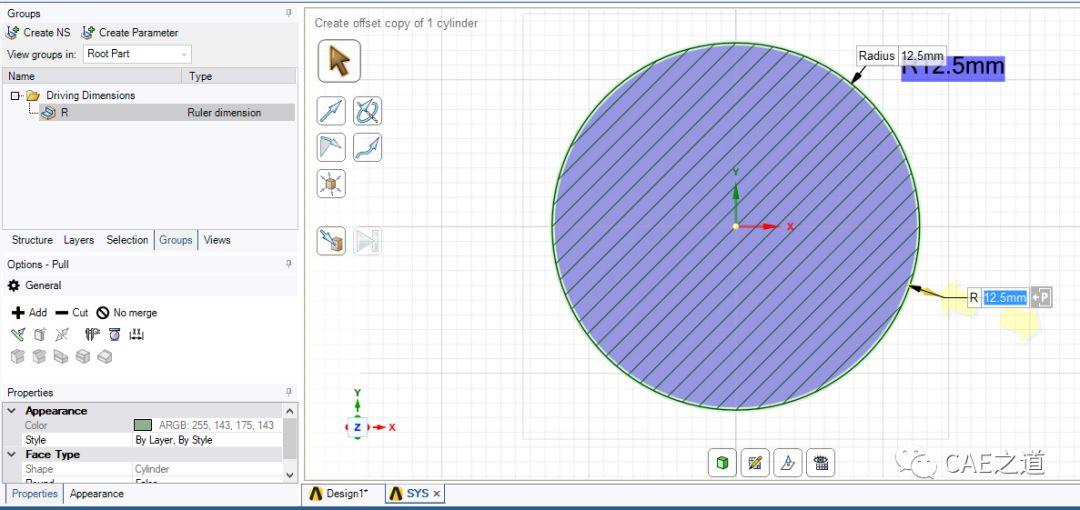
③建立杆模型:点击Prepare→Profiles→Crate,选择草绘的两条线,建立杆模型。
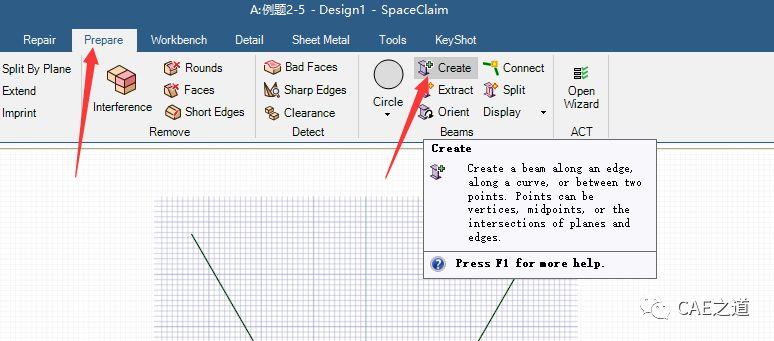
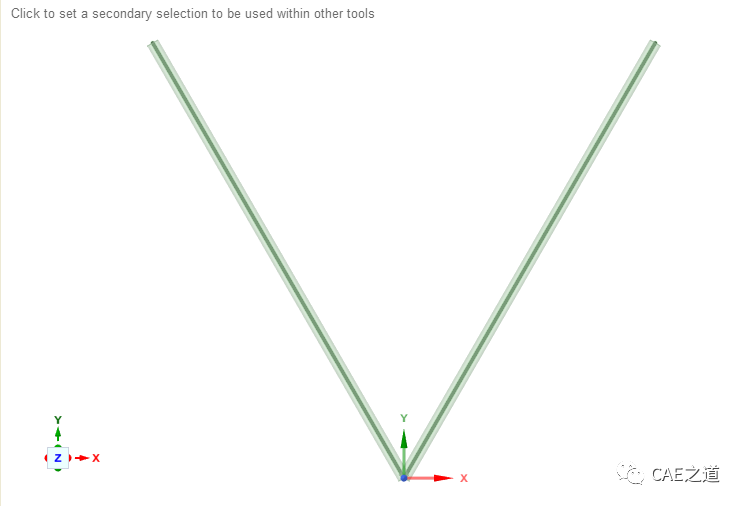
④共享重合拓扑。使用WB的share命令,在两杆连接点进行共节点处理。至此,几何模型建立完毕。
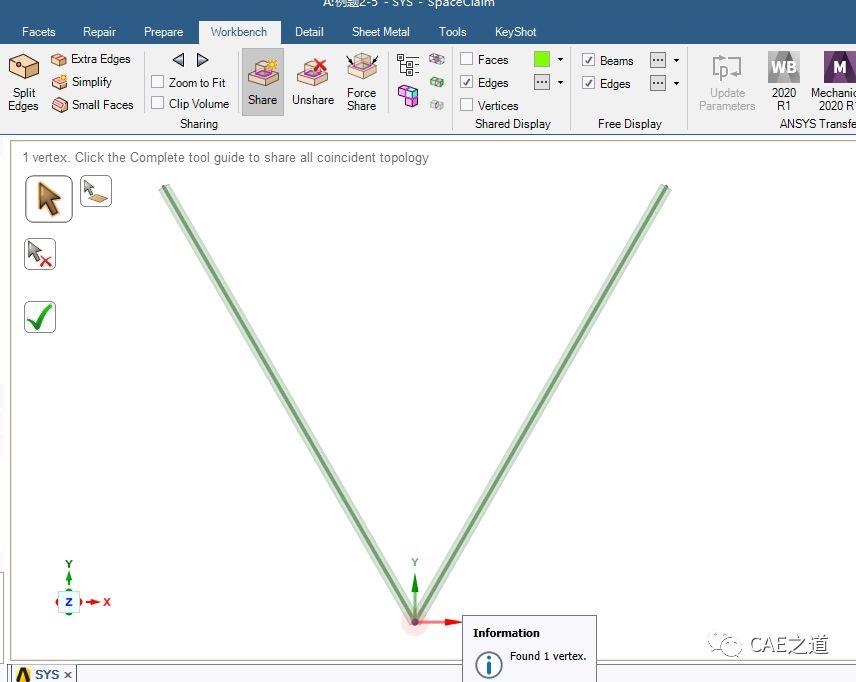
Step4:双击A4 Model进入Mechanical。Step5:更改材料。点击Beam(Circle),在Details of Beam(Circle)中,将Material中的Assignment更改为“例题2-5”,表示我们将材料设置为之前新建的“例题2-5”材料。此处如果不更改材料,软件将默认使用结构钢进行计算。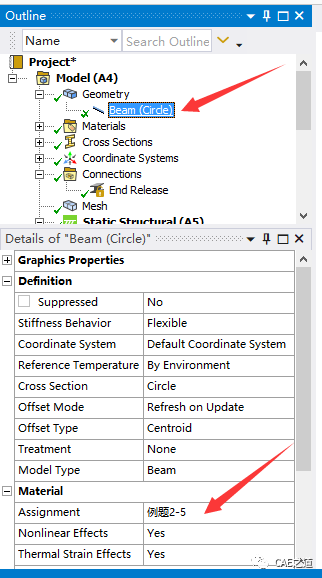
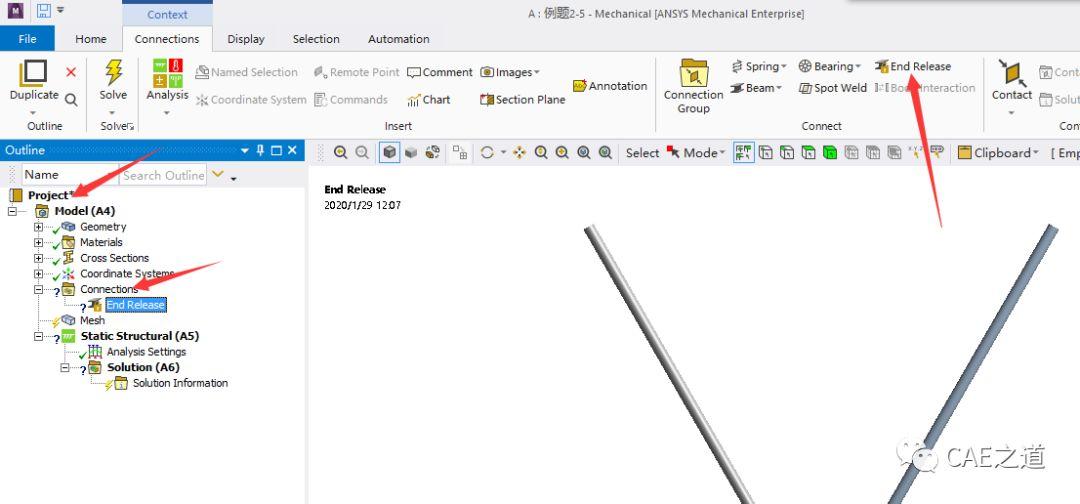
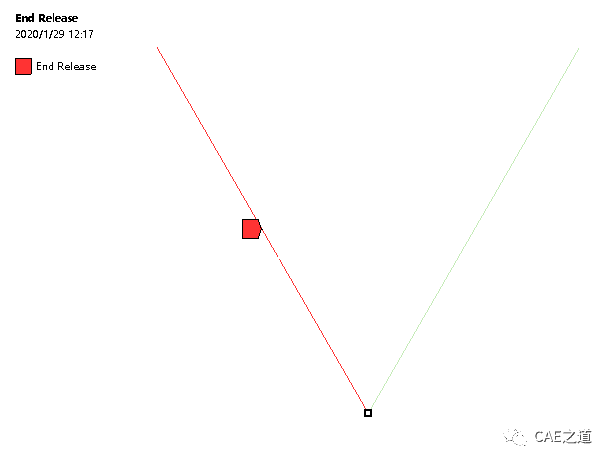
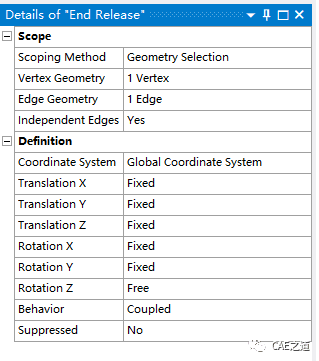
Step6:设置两杆铰接。因为在建模时,我们对模型进行了共享拓扑,若不设置铰接,在两杆连接处就不存在相对运动,类似于将两杆焊在一起。在Project中点击Connections,选择End Release,在Details of End Release中,将Scope中的Vertex Geometry选择为两杆铰接点,Edge Geometry选择为其中的一根杆,将Definition中的Rotation Z设置为Free,表示我们释放z轴的转动自由度。至此,铰接设置完毕。
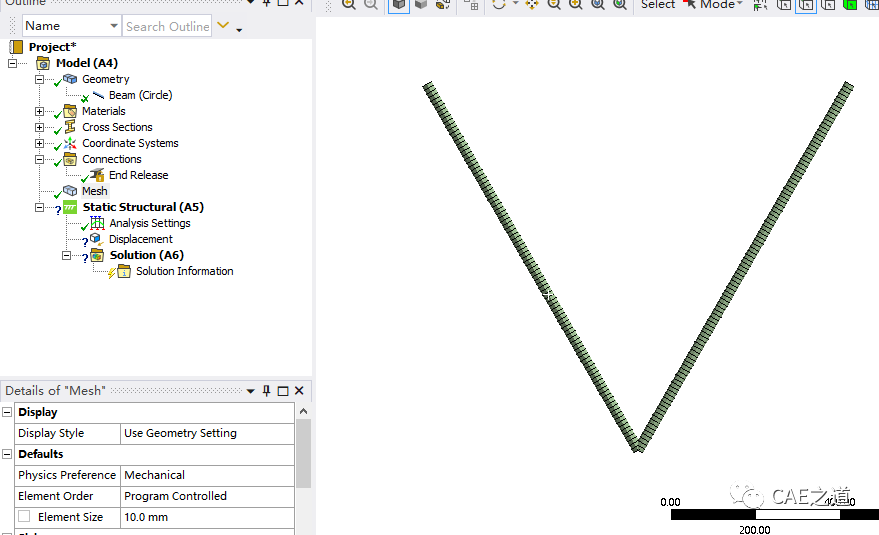
自由网格划分,网格尺寸设置为10mm。由于建立的是线体模型,WB在网格划分时自动赋予BEAM188单元;
载荷:施加在A点,大小为100kN,方向竖直向下。
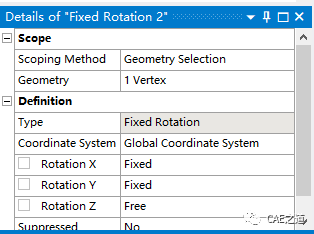
约束:B、C两点,只释放绕z轴的旋转自由度,约束其他五个自由度。处理方式为每点施加一个Simply Supported和一个Fixed Rotation约束,其中Fixed Rotation约束将Rotation Z设置为Free(如下图二)。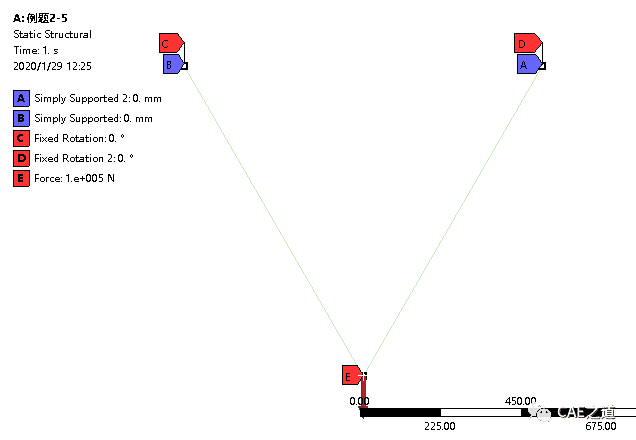
Step9:求解及后处理。
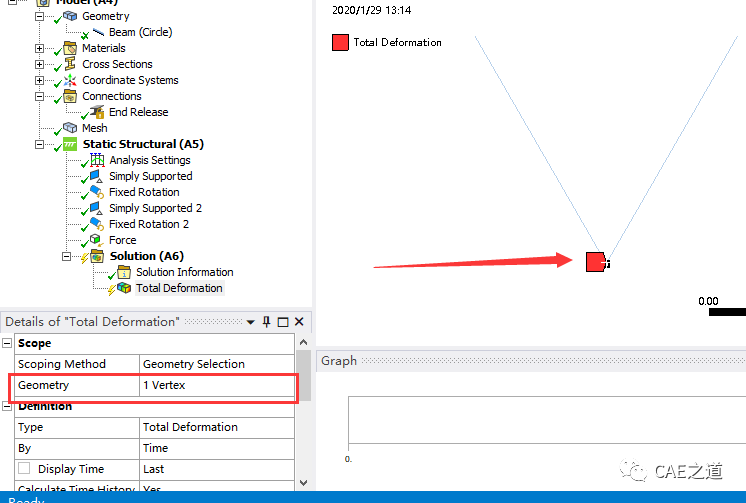
该例题我们主要计算节点A的位移。选择Results→Deformation→Total,在Details of Deformation中,将Scope中的Geometry选择为节点A,如下图二所示,最后右击Solution(A6),选择Eevaluate All Results,提取结果。计算结果如下图三。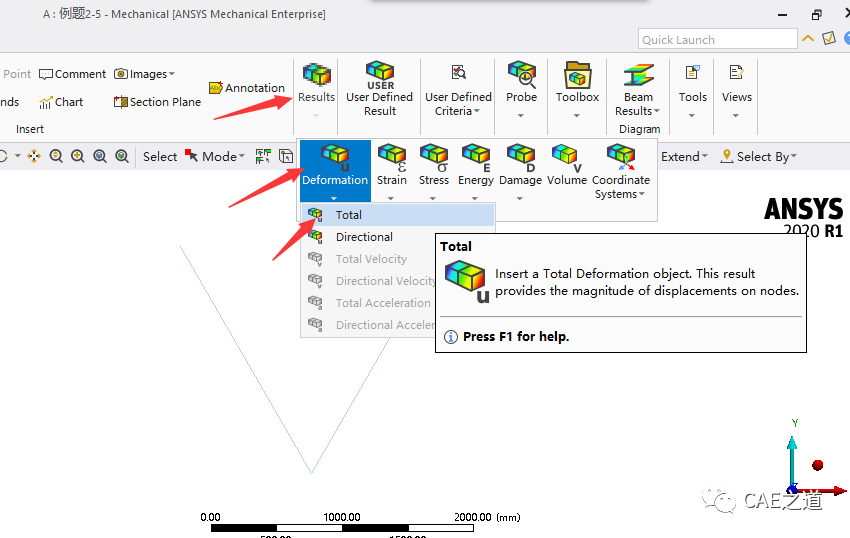
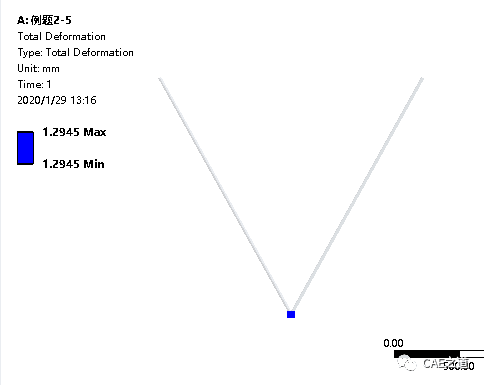
①材料力学方法计算结果为1.2934mm,ANSYS计算结果为1.2945mm,结果基本一致。但材料力学计算方法使用小变形假设,在作图求位移时,也进行了一定的简化计算,所以ANSYS的计算结果应较为准确。②材料力学中小变形假设,计算误差在可接受范围以内,但计算效率却得到了很大的提高。
③该题还可使用弹性体的功能原理进行方便快捷的计算,ANSYS也可计算结构中的应变能,该方法将在下一篇文章中为大家讲解。