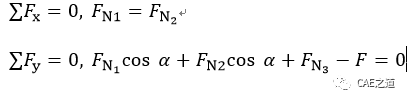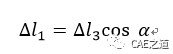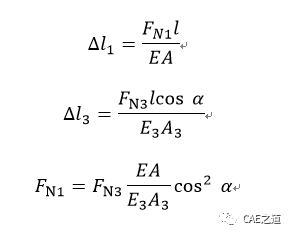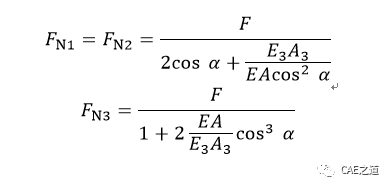超静定问题之三杆桁架问题
本文摘要(由AI生成):
本文介绍了求解三杆铰接结构轴力的两种方法:材料力学方法和有限元解法(ANSYS)。首先通过材料力学方法,建立静力平衡方程和变形几何相容方程求解轴力。随后,使用ANSYS进行有限元分析,通过建模、材料设置、建立运动副、网格划分、约束和载荷设置等步骤求解轴力。两种方法得出的结果一致,验证了求解的正确性。
我们之前所讨论的杆、梁结构,其约束反力或者构件内力都能通过静力学的平衡方程求解,这样的问题我们称为静定问题。
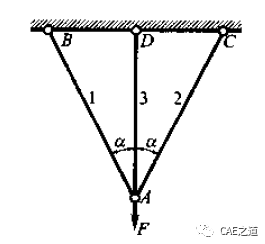
但在实际工程中,出于对结构安全性的考虑,往往采取更多的构件或支座。例如大型承重桁架中某一结点由三杆铰接而成(如下图),由于平面汇交力系仅有2个独立的平衡方程,显然,仅由静力学平衡方程不可能求出3个未知轴力。这类不能单凭静力学平衡方程求解的问题,称为超静定问题或静不定问题。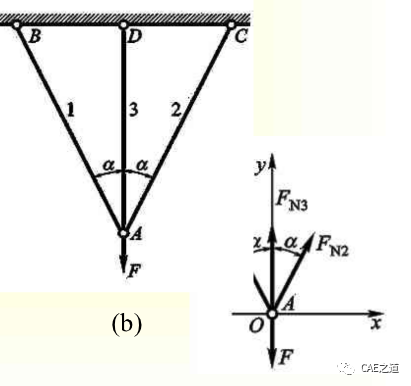
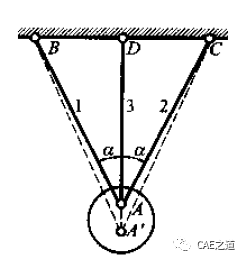
在超静定问题中,都存在多于维持平衡所必需的支座或杆件,习惯上称其为“多余”约束。由于多余约束的存在,未知力的数目必然多于独立平衡方程的数目。未知力数超过独立平衡方程数的数目,称为超静定次数。与多余约束相应的支反力或内力,习惯上称为多余未知力。因此,超静定的次数就等于多余约束或多余未知力的数目。求解超静定问题时,需要综合运用到静力学平衡条件、物理关系和变形几何相容方程。所谓变形几何相容方程,就是依据变形的几何相容条件建立的,而变形(或位移)与力(或其他产生变形的因素)间具有一定的物理关系,将物理关系代入变形几何相容方程,即可得补充方程。将静力平衡方程与补充方程联立求解,就可解出全部未知力。下面我们以一个三杆铰接结构为例,使用材料力学和有限元解法分别求解。设1、2、3三杆用铰连接如下图所示。已知三杆的的材料相同,弹性模型E=200GPa,截面半径均为5mm,中间杆杆3的长度为100mm,杆3与杆1、2的夹角均为20°。铰接点受到沿铅锤方向的外力F=1000N。求三杆的轴力。
一、基于材料力学方法的计算:
求解超静定问题时,需要综合运用到静力学平衡条件、物理关系和变形几何相容方程。
受力分析,受力图如下,根据受力图,列出平衡方程。
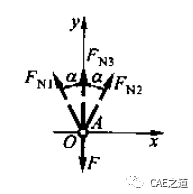
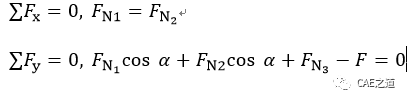
杆系共有三个汇交于A点的未知轴力,但平面汇交力系仅有2个独立的衡方程,故为一次超静定,需寻求一个补充方程。
根据变形相容条件建立变形几何方程。由于三杆在下端连接于A点,故杆在受力变形后,其下端仍应连接在一起,如A'点。由于问题在几何、物性及受力方面的对称性,且已假设三杆轴力均为拉力,故A点位移应铅垂向下。1、2杆的伸长量ΔL1与杆3伸长量ΔL3之间的关系如下图所示。
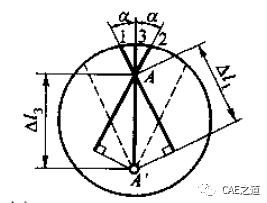
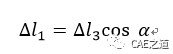
在线弹性范围内, 变形ΔL1、ΔL3与所求轴力FN1、FN3之间的物理关系式为: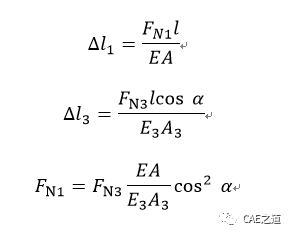
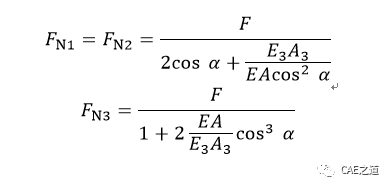
二、基于ANSYS的计算:
使用ANSYS求解该问题时,我们从以下几个方面入手:
1. 确定分析类型:根据例题所示结构,确定分析类型为静力学分析;2. 确定单元类型:该结构为梁结构,结果需要输出轴力,因此分析时使用Beam单元。
根据例题中提供的梁模型尺寸,我们在SCDM中建立梁模型。
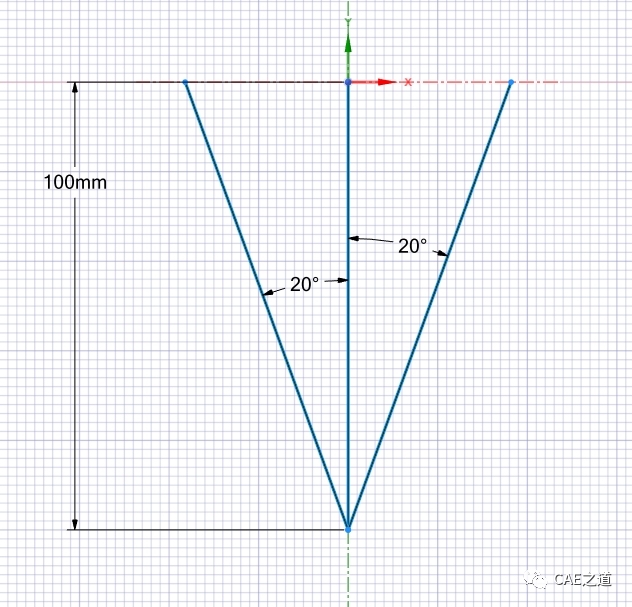
建立一个半径为5mm的圆形截面,并将截面赋予给结构草图,建立完成的梁结构如下图所示:

打开Workbench,选择Static Structural模块,并传入上一步建立的几何模型。
本次分析使用默认的结构钢材料。软件自带的结构钢材料,弹性模量为200GPa。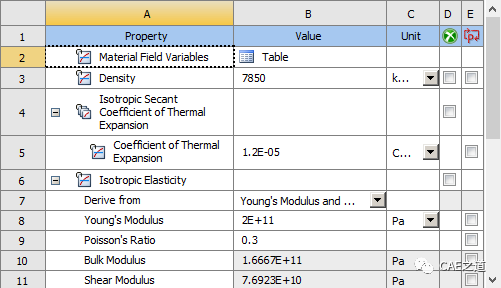
由于三杆连接处为铰接,所以需在连接位置建立转动副。由于一个转动副单元只能连接两个节点,所以我们至少需要再此处建立两个转动副。
我的建立方法是:在杆1、2之间建立一个转动副;在杆2、3之间建立一个转动副,建立时应注意旋转轴是否与实际结构对应。建立好的运动副如下图所示:

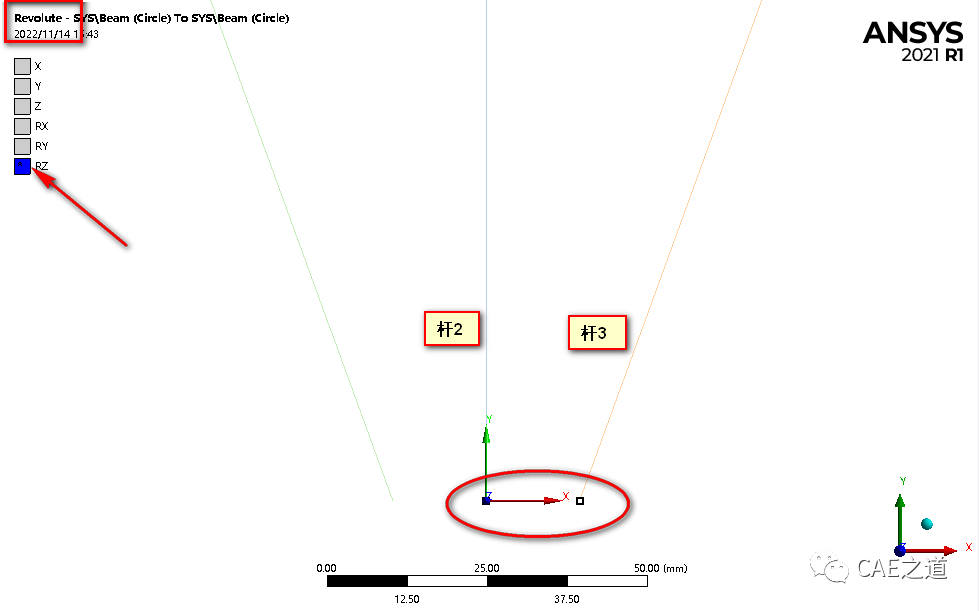
Tip:需要建立运动副的三个点是重合的,虽然ANSYS提供了重合点选择的方法,但我们想确定点是否选择正确,却不太直观。此时我们可以使用Display中的Explode选项卡,拖动按钮,可以将结构拆分显示。

根据题意,约束B、C、D三点的三个平动自由度和沿X轴、Y轴的转动自由度,仅释放沿Z轴的转动自由度。在Workbench中,可以在B、C、D三点使用Simple Support(固定3个平动自由度)和Fixed Rotation(释放Z轴转动)组合实现。设置的约束如下图:
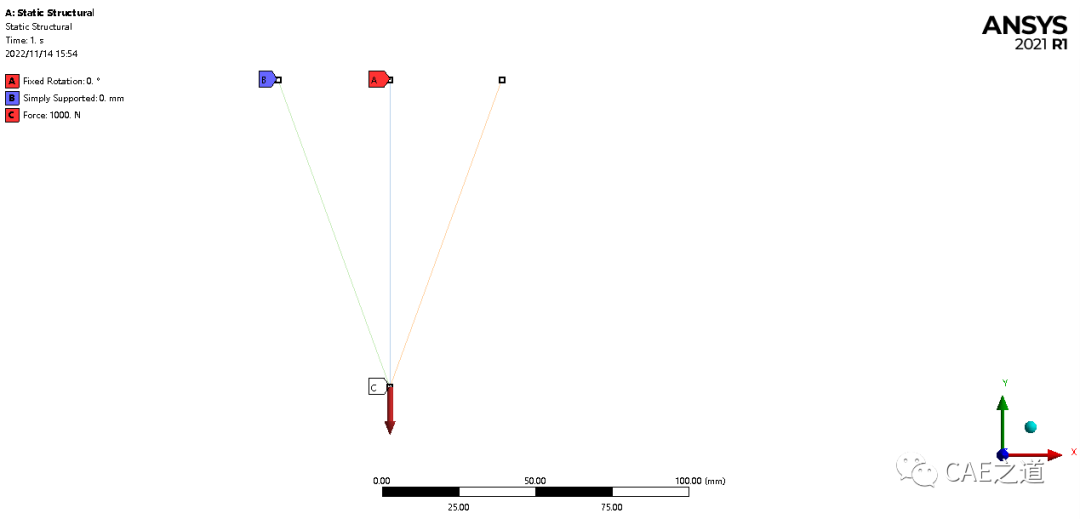
根据题意,载荷是作用在A点的1000 N的集中载荷,可通过Force实现。

求解设置全部保持默认。
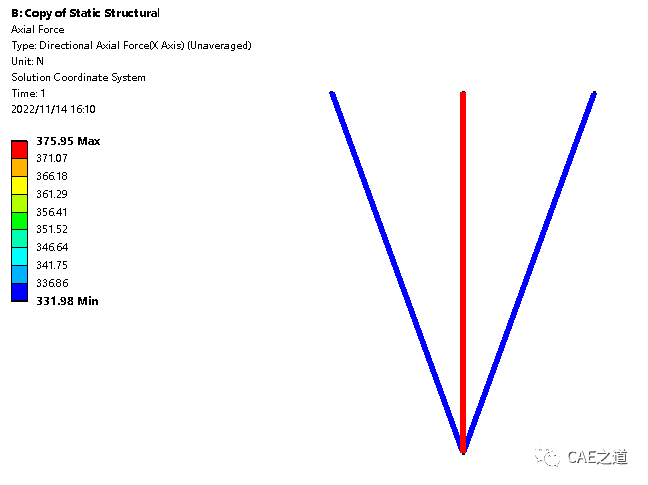
点击Beam Results,选择Axial Force(轴力),然后求解。

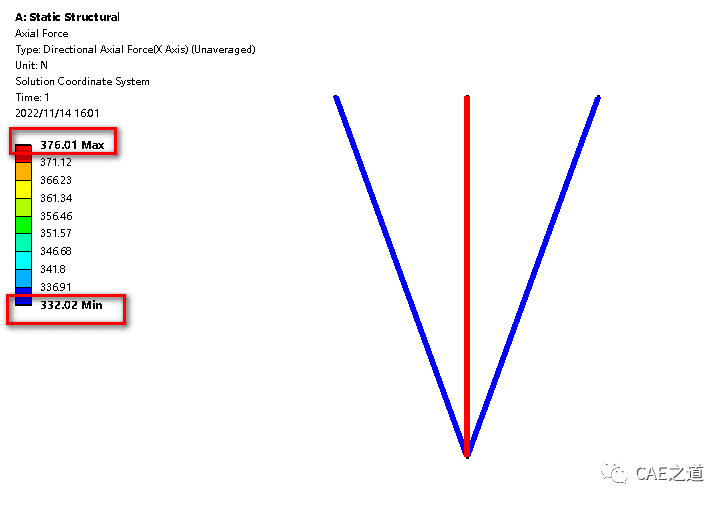
上述结果读者可以自行计算。由此可见,使用有限元计算方法与材料力学公式算出来的完全一致。我们之所以在三杆连接处建立运动副,是为了使有限元模型更接近于真实结构。如果我们直接将三杆连接处做共节点处理,计算结果(见下图)与建立运动副的几乎一致。这是因为这个结构整个变形较小,杆之间的夹角在受力前后变化不大,使得计算出的轴力也相差不大。使用的材料力学计算公式,实际上也是基于小变形假设。