Ansys Lumerical | 针对 CMOS image sensor 仿真中的角度响应
说明
在本例中,通过使用FDTD求解器和CHARGE求解器对CMOS图像传感器的光学和电学特性进行仿真,从而分析其角度响应。仿真的结果主要包括:光的空间分布与传输,光效率及量子效率与光入射角度的关系,同时还分析了微透镜位移产生的影响。
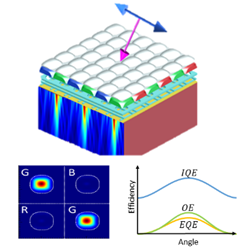
综述
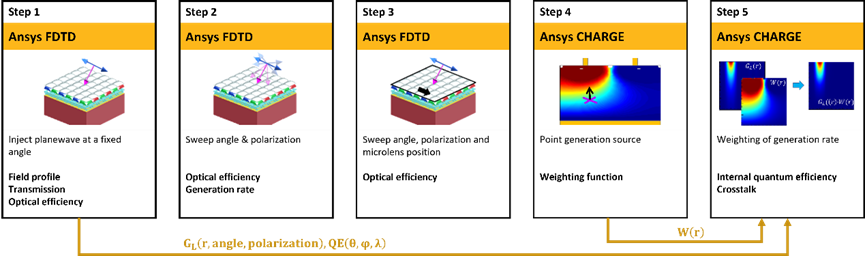
CMOS图像传感器在亚波长范畴的吸收、散射和衍射及电荷的运动特征,通常需要联合其光学与电学特性来仿真分析。因此,在本例中光学仿真将用于求解光场的分布、传输和效率等结果,同时仿真还分析了光入射角度和位移的影响。随着步骤1-3中参数个数不断增加(单模拟、角度/偏振扫描和角度/偏振/微透镜位置的扫描),案例将分析不同参数与结果的复杂关系。最终,基于光学仿真(步骤2)得出的电荷生成数据将与电学仿真(步骤4)得出的加权函数相结合,分析求解出不同入射角度下的量子效率和串扰(步骤5)。
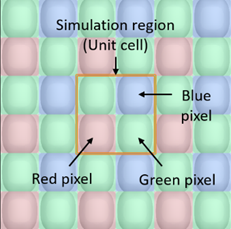
注解:“像素(pixel)”的定义可能因应用领域而有所区别。在本例中,光学仿真区内有一个周期单元(unit cell),一个单元中有红/绿/蓝/绿四个像素,我们将周期单元中包含的红/绿/蓝/绿结构称为“像素”。这意味着一个单元中有4个像素,如下图所示。
步骤1:初始仿真
模型中的传感器以固定角度被平面波照射,运行仿真FDTD求解器将获取每个像素中的场分布、传输和光学效率。在此步骤中将得到以下结果:
光场分布 Field profile
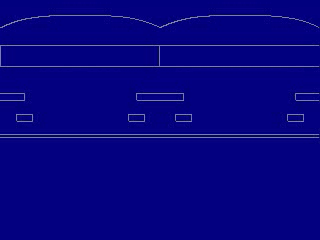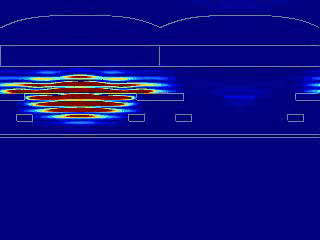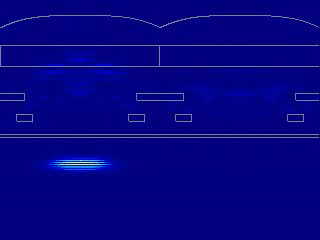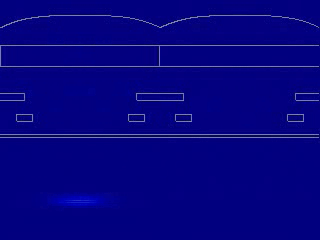
场监视器将分别记录红/绿色像素和绿/蓝色像素横截面上的光场分布。因为光源的波长被设置为550 nm(绿色),由于不同区域的波长选择性不同,所以可以发现下图中绿色像素处的监视器中的透射较高。
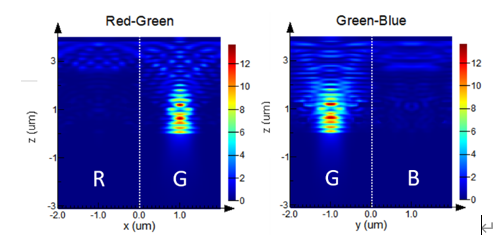
传输效率 Transmission
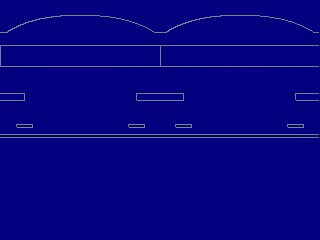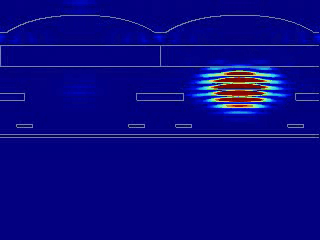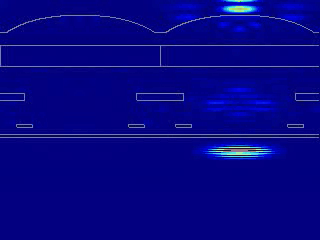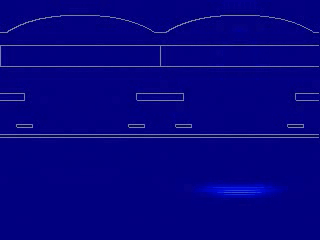
为了计算每个像素吸收的能量(光学效率),我们可以选择仅在像素的耗尽区域上计算硅表面处坡印廷矢量在法线方向的分量Pz的积分。若想在目标区域计算Pz的积分,最简单方法是使空间滤波器(场监视器)的尺寸与耗尽区域相同,再将其与Pz分量相乘。下图分别是未过滤的Pz分量、耗尽区域和耗尽区的Pz分量。本例中,每个耗尽区的形状接近一个1x1um正方形,但带有圆角。

光学效率Optical efficiency
光学效率定义为像素耗尽区域中吸收能量与光源发出能量的比值,定义为:

通过对硅表面的Pz分量进行积分,与光源发出的总能量进行归一化,可以发现约38%的能量被传输到硅层中。其中,两个绿色像素的综合效率约为33%,而红色和蓝色像素的效率分别约为0.5%。

步骤2:角度响应
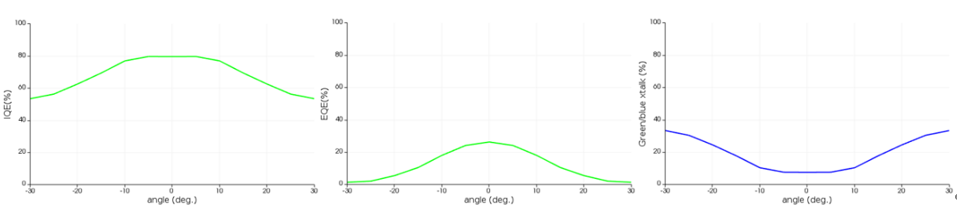
此步骤计算了光入射角度与光学效率和电子-空穴对生成速率的关系。在此例中,生成速率结果将在y方向上求平均后以2D格式保存,以便兼容步骤5中的2D电学模型,来计算器件的量子效率。
文件扫包含14个扫描点,由光源的7个入射角度和同一角下的2个极化方向交叉而成。在此步骤中将得到以下结果:
光学效率
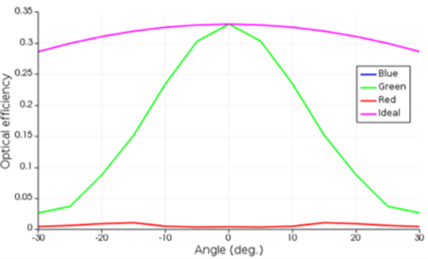
不同像素的光学效率与光源入射角度的关系如下所示。从结果可以发现,绿色光源的光效率在正入射时最大,在较大的入射角时减小。此外,角度响应仿真还提供了光学串扰的测量方法,从图中可以发现在绿色光源下,有部分光能量被红色或蓝色像素吸收了(反之亦然)。
产生速率 Generation rate
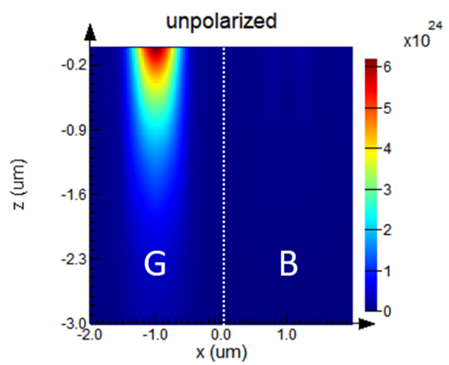
扫描完成后将创建14个包含绿色/蓝色像素生成速率的数据文件。下图显示了绿色/蓝色像素中非偏振光(550 nm)的生成速率。本示例收集的是“y”方向上的平均生成速率,并通过脚本生成其在方向GL(x,z)上的2D平均映射。这样做的目的是使生成的2D生成速率与步骤4中CHARGE的2D仿真模型相兼容,从而节省电学仿真阶段所需要的时间。
步骤3 :微透镜位移
本步骤中将计算出光学效率与光源入射角度及微透镜位移关系的2D数据图。
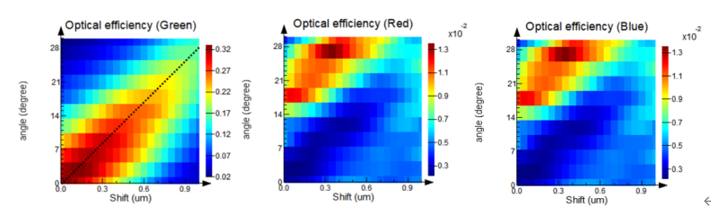
扫描总共包括462个扫描点,由21个不同的微透镜位移和对应的2个偏振下的11个光源入射角度组成。下图展示了每个像素在不同光源角度和镜头偏移时的光学效率。从绿色像素的结果可以看出不同入射角度下的最大光学效率,如黑色虚线标记所示,位移随角度的偏移量约为37nm/度。例如,如果光线以15度入射时,透镜需要移动约555 nm以获得最大光学效率。
步骤4:加权函数
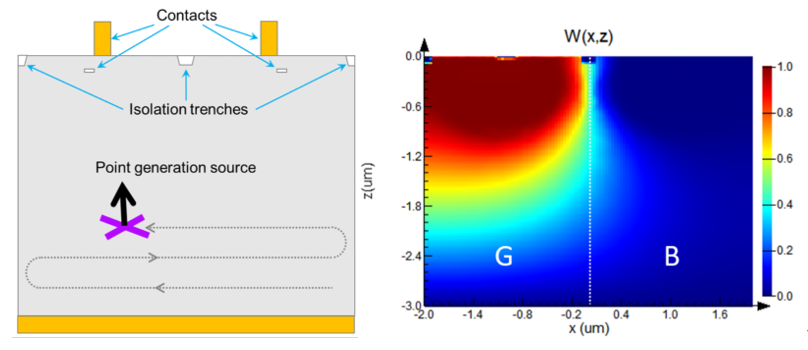
运行CHARGE求解器以获得系统对基板中任意位置的电子-空穴对的脉冲响应(格林函数 Green’s function)。由此,我们计算了一个空间变化的加权函数,该函数表示在空间中任何点生成的电子-空穴对被特定像素的触点收集的概率(本例中为绿色)。
在这一步中,我们在CHARGE仿真中使用point generation source来确定器件的加权函数W(x,y,z)。W(x,y,z)表示对应位置产生的电荷被特定触点收集的概率。这种方法基于格林函数G(x,y,z),通过分析可得每个触点响应特定位置脉冲源时的载流子密度n,p。
载流子密度是通过仿真电荷运动分析出来的。为了确定完整的格林函数G(x,y,z),根据脚本的指令,脉冲源的位置将沿着路径r不断移动,扫过整个仿真区域。下图显示了绿色像素的加权函数W(x,y,z),表明当电荷靠近绿色触点(左上角)时,绿色像素的收集概率非常高。然而,它还表明,在蓝色像素区域(x>0)产生的一些电荷被绿色触点收集的概率并非零。这表明相邻像素之间存在一定的串扰串扰。
步骤5:内部量子效率和串扰
在这一步中,我们将基于格林函数方法计算绿色像素的量子效率(QE)和绿色/蓝色串扰。相关数量的定义如下:

量子效率和串扰:
依次加载步骤2中从不同角度扫描得到的14份生成速率数据,并将其与绿色像素的加权函数相乘。下图显示了常规角度入射时,非偏振光的GL(x,z)、Wgreen(x,z)和GL(x,z)*Wgreen(x,z)。
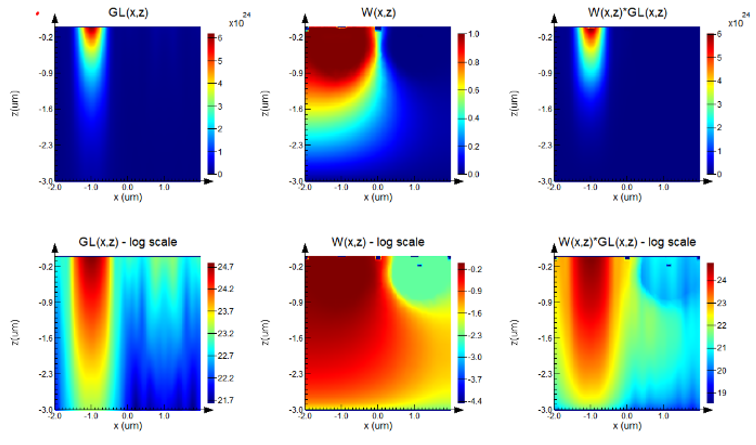
通过对GL(x,z)*Wgreen(x,z)进行积分并将其与总生成速率进行归一化,我们获得了绿色像素的IQE。对蓝色像素Wblue(x,z)的加权函数重复相同的过程,会产生绿色/蓝色串扰。IQE的最大值约为80%,在较大的光源角度下会数值将会减小。这一趋势与绿/蓝串扰在更大角度上的增加相一致,最大EQE约为26%。