能量误差分析中各个数据的意义
在midas MeshFree中,提供了与准确性相关的能量误差分析,它是基于应力误差定义的应变能误差,为分析结构化网格尺寸带来的误差提供依据。
应变能公式:
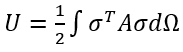
能量误差公式:

其中,e为应力误差向量。
线性静力分析完成后,在后处理中可以看到[能量误差分析]功能。

下面用一个简单的例子说明[能量误差分析]功能。

该模型由两块长方体板组成,大长方体的尺寸是400mm×100mm×10mm,小长方体的尺寸是100mm×100mm×5mm。模型左端固定,右端面受到向下1000N力的作用。计算完成后,点击[能量误差分析],可以看到如下窗口:

图1 应变能和能量误差数据
有工程师反映看不懂这些数据,下面我们就梳理一下这些数据的关系吧~
能量密度平均值是指部件的单位体积应变能;
能量误差密度平均值指部件的单位体积能量误差;
应变能总和指所有部件的应变能之和;
能量误差总和指所有部件的能力误差之和;
能量百分比指部件的应变能与应变能总和之比;
能量误差百分比指部件的能量误差与能量误差总和之比;
大长方体的尺寸是400mm×100mm×10mm,因此体积为400000mm³,它的能量密度平均值是0.0291J/mm³,能量误差密度平均值是5.16e-6 J/mm³,因此
应变能:U大=400000mm³×0.0291J/mm³=11640J
能量误差:UE大=400000mm³×5.16e-6 J/mm³=2.064J
小长方体的尺寸是100mm×100mm×5mm,因此体积为50000mm³,它的能量密度平均值是0.0146J/mm³,能量误差密度平均值是5.57e-6 J/mm³,因此
应变能:U小=50000mm³×0.0146J/mm³=730J
能量误差:UE小=50000mm³×5.57e-6 J/mm³=0.2785J
应变能总和U= U大+U小=12370J
能量误差总和UE=UE大+ UE小=2.3425 J
大长方体的能量百分比= U大/U=11640/12370≈94.1%
大长方体的能量误差百分比= UE大/UE=2.064/2.3425≈88.1%
小长方体的能量百分比= U小/U=730/12370≈5.9%
大长方体的能量误差百分比= UE大/UE=0.2785/2.3425≈11.9%
计算结果均与程序给出的结果一致,见图1。
图1中还有1个数据是归一化总误差,表达为:

因此分析的归一化总误差为:

计算结果也与程序给出的结果一致,见图1。
现在大家应该清楚这些数据之间的关系了吧~下一篇将说明如何利用这些数据进行结果评价。