midas 动刚度
刚度是指结构或材料抵抗变形的能力。由于结构或材料所受荷载的不同,可能受到静载荷或动载荷,因此,刚度又分为静刚度和动刚度。当结构或材料受到静载荷时,抵抗静载荷下的变形能力称为静刚度;当受到动载荷时,抵抗动载荷下的变形能力称为动刚度。故,结构或材料既有静刚度又有动刚度。
了解动刚度原理之前,先了解一下FRF(Frequency Response Function)
频率响应分析是一种确定线性结构在承受一个或多个(相同频率)简谐载荷作用下系统稳态响应的的技术。它只计算稳态受迫振动,不计算激励开始时的瞬态振动。我们已经明白了频响函数可以用位移/力表示,当用力/位移时,表示的是动刚度。我们同时测量激励力和由该激励力引起的结构响应(这个响应可能是位移、速度或加速度),将测量的时域数据通过快速傅立叶变换(FFT)从时域变换到频域,经过变换,频响函数最终呈现为复数形式,包括实部与虚部,或者是幅值与相位。公式形式如下:




单自由度动刚度

而动刚度为力与位移之比,则
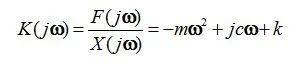
从上式可以看出动刚度:
1) 复值函数;
2) 随频率变化;
3) 与系统的质量、阻尼和静刚度有关;
4) 当频率等于0时,动刚度等于静刚度;
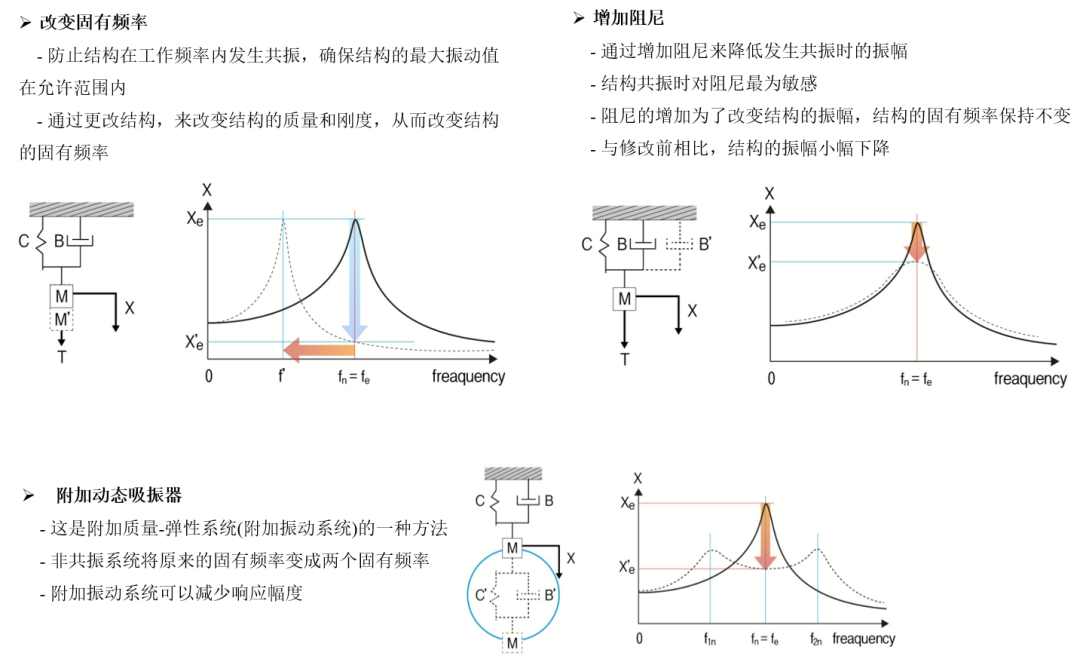
让我们再回想一下单自由度系统的FRF区域及性质

同理,单自由度系统的动刚度曲线也有类似性质

在低频段,动刚度接近静刚度,幅值是k,表明共振频率以下的频率段主要用占主导地位的刚度项来描述。如果作用在系统的外力变化很慢,即外力变化的频率远小于结构的固有频率时,可以认为动刚度和静刚度基本相同。
在高频段,动刚度的幅值为ω2m,表明共振频率以上的频率段主要用占主导地位的质量项来描述,这是因为质量在高频振动中,产生很大的惯性阻力。当外力的频率远大于结构的固有频率时,结构则不容易变形,即变形较小,此时结构的动刚度相对较大,也就是抵抗变形的能力强。
在共振频率处动刚度的幅值下降明显,其幅值为ωc,表明在共振频率处主要受阻尼控制。而在共振频率处,我们知道,结构很容易被外界激励起来,结构的变形最大,因而结构抵抗变形的能力最小,也就是动刚度最小。
多自由度动刚度
单自由度系统是基础,但现实世界中的系统大多数都是多自由度系统,因此,我们测量出来的动刚度也是多自由度的动刚度。下图为多自由度系统的同一位置的加速度频响函数(加速度导纳)和该点的动刚度曲线。

多自由度系统的驱动点FRF存在多个共振峰和反 共振峰,在共振峰处,对结构施加很小的激励能量,结构就会产生非常大的振动(变形),因而在共振峰处,结构很容易被激励起来,结构的变形大,抵抗变形的能力弱,也就是动刚度小。
在反 共振峰所对应的频率处进行激励,即使激励能量再大,结构也没有响应或者响应很微弱,也就是说在**振峰所对应的频率处,结构很难被激励起来,结构的变形小,抵抗变形的能力强,因此,动刚度大。
从上图可以看出,频响函数共振峰对应的是动刚度曲线的极小值,也就是说频响函数幅值大的频率处,动刚度小。在反 共振峰处,动刚度大,二者刚好相反。参考文献:知乎up主linmue-谭祥军
频率响应分析又称扫频分析:计算结构在简谐载荷作用下对每个计算频率的响应幅值和相位,确定结构响应最敏感的频率范围,即共振点。
用于频率响应分析的荷载是正弦荷载(谐波荷载)。模态分析可以得到结构的固有频率和振型,尽管能够判断结构在频率荷载作用下发生共振的可能性,但是难以获得连续的响应结果。
频率响应分析是一种线性分析,任何非线性即使定义也会被忽略。
频率响应分析定量地表达了设计产品对每个频率的响应,因此,可以清楚地看到每个频率荷载下结构的变形。例如,在汽车中,发动机转速(转数可以转换为频率)发生变化时,从正常空转状态逐渐增加转速,安装在车辆中的很多部件随着频率的变化呈现出各种动态响应。下图是频率位移曲线图,明显地看到,在一定的激励频率下,位移增加,而在其他激励频率下,位移减少。

举例:以MeshFree为例:NFX请参考相应操作例题



载荷定义

直接法分析控制定义


频率集的定义
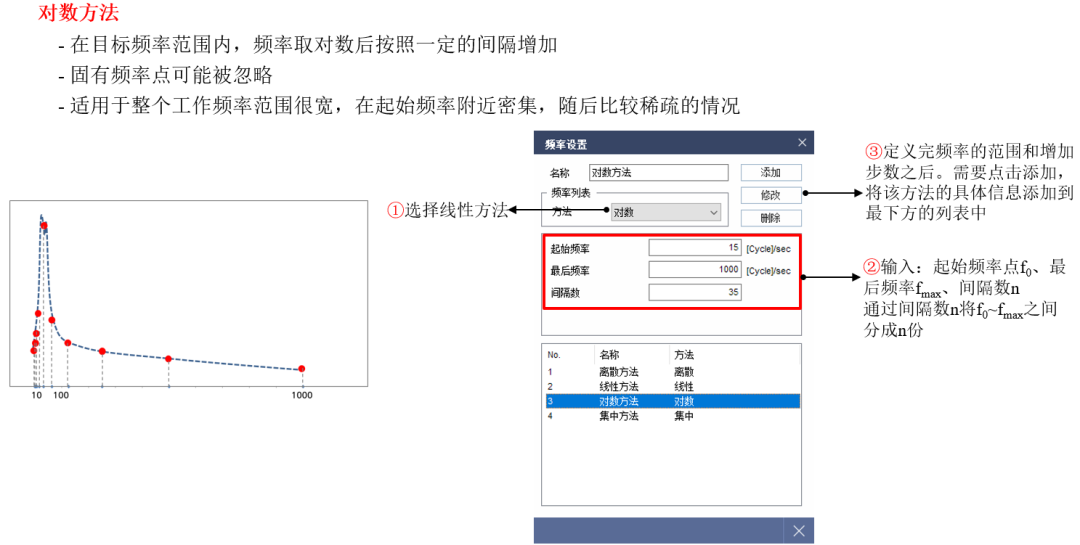
频率集的定义是频率响应分析中至关重要的一环。我们知道,前面添加频率依存载荷的时候,定义了简谐载荷的幅值和相位,这一部分将定义简谐载荷的频率变化范围,这也是频率响应分析又被称为扫频分析的原因。
MeshFree提供离散、线性、对数、集中等4种频率集的定义方式,也可以组合使用。



结果查看 查看各点的频率响应结果

控制措施