基于有限体积法和有限元法的商用软件离心泵计算流体分析

基于有限体积法和有限元法的商用软件离心泵计算流体分析
ComputationalFluidDynamicSimulationsofaCentrifugalPumpUsingCommercialSoftwarebasedonFiniteVolumeMethodandFiniteElementMethod
저자(Authors)
이석근,손일엽
SeokkeunYi,IlyoupSohn
출처(Source)
발행처(Publisher)
한국CDE학회논문집24(2),2019.6,192-202(11pages)
KoreanJournalofComputationalDesignandEngineering24(2),2019.6,192-202(11pages)
(사)한국CDE학회
SocietyforComputationalDesignandEngineering
版权指南
DBpia提供的所有著作物的著作权归原作者所有,NuriMedia不保证或承担各著作物的责任。另外,DBpia提供的著作只有与DBpia签订订阅合同的机关所属用户或该著作的个别购买者才能非盈利地使用。因此,违反此规定,擅自使用DBpia提供的著作物时,可根据相关法律承担民事、刑事责任。
基于有限体积法和有限元法的商用软件离心泵计算流体分析
이석근1·손일엽1,2†
1韩国科学技术研究院信息虚拟设计中心,2科技大学研究生院数据与HPC科学
ComputationalFluidDynamicSimulationsofaCentrifugalPumpUsingCommercialSoftwarebasedonFiniteVolumeMethodand
FiniteElementMethod
一、简介
离心泵广泛应用于工业。
1.FVM和FEM的定理
2.1有限体积法(FVM)
2.1.1有限体积法的理论与特点

Fig.1有限体积法中的空间离散化
它是划分为受控体积(controlvolume)的过程。由于检测体的边界(或表面)位于相邻节点的中点,因此每个节点如图1所示。如图1所示,它被一个控制体或网格包围,偏微分形式的输运方程可以离散化为方程(1)。一般来说,检查体设置在流域的边缘,使物理边界与检查体边界重合。第二步是有限体积法的核心步骤,将控制体积中的控制方程积分,推导出节点P处的离散方程。对于等式(1)中定义的控制体积横截面积,V是体积,S是测试体积的小值它是标准S的平均值。有限体积法的一个特点是离散方程具有如下清晰的物理解释。换言之,控制体积中的φ的守恒方程形成为从东侧离开的扩散通量φ减去进入西表面的扩散通量φ等于生成的φ。需要扩散系数和斜率来导出有用形式的离散化方程。通过这个,在节点处定义和计算φ的值和扩散系数。为了计算检查体平面内的梯度,利用节点间的分布特性,线性逼近是最简单的方法,也称为中值差分法。此外,对离散方程进行了修改,将边界条件包括在与流域边界相邻的控制体积中,因此,可以通过求解离散线性代数方程[14]来获得每个变量的分布。

2.1有限元法(FEM)
2.2.1有限元法的理论与特点
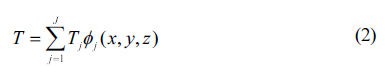
有限体积法(FVM) | 有限元法(FEM) | |
好处 | -即使在具有强非线性的问题中也具有出色的助焊剂保持性。 | - 适用于各类偏微分方程 高阶 -易于应用离散化。 |
坏处 | -难以应用高阶离散化方法 | -与有限体积法相比,很难推导出这个氧化方程。 |
有限元方法分两步离散,虽然两步都可能出现数值误差,但并不总是出现附加误差。第一步,逐段插值,是将局部解与离散有限元中的节点值连接起来。第二步是使用加权残差结构将代数方程与节点值的解联系起来。这样,有限元公式就形成了[23]。表1总结了这些FVM和FEM的优缺点。
3.1问题定义
离心泵的工作形式是水流入叶轮,流体通过叶轮叶片的旋转通过蜗壳排出,分为蜗壳部分,将能量转化为压力能。
在这项研究中,叶轮由总共6个螺旋形叶片组成。为了模拟由于叶轮旋转引起的流体动能传递效应,将叶轮和蜗壳分为两部分进行建模,并将相同的形状应用于FLUENT和NFX。假设工作流体为25℃水,密度为998.2kg/m3,粘度为1.003×10-3kg/m·s。
3.1建模概述
本研究中使用的离心泵参考了ANSYSFLUENT[24]提供的离心平板泵CFD教程中呈现的形状。根据定义对边界条件和形状进行建模.
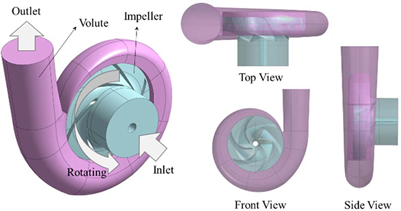
叶轮入口段直径为0.169m,蜗壳出口段直径为0.136m,叶轮每个叶片为螺旋几何形状,叶尖厚度为0.0141m。
叶轮和蜗壳的几何形状如图1所示。如图2所示,旋转部分和固定部分是分开建模的,在实际流动分析中,它被建模为可以给旋转部分叶轮一个相对速度。
3.1.1 数值分析技术
在这个离心泵分析问题的情况下,在FLUENT和NFX中都使用了多参考系(MRF)技术,以使用相对速度来反映旋转现象,而无需实际旋转网格。叶轮的旋转速度设定为从叶轮的中心轴以1,450rpm旋转。另外,在压力-速度耦合中,FLUENT采用耦合法,NFX采用分离法。每种技术的使用细节内容等,应在对每个SW的分析过程中再次说明。
4.1.FVM基于流量分析的概述
FVM在此基础上使用ANSYSFLUENT18.1版本进行流动分析,进行3D分析,精度达到双精度。
4.1.1 创建网格
在FLUENT的情况下,如3.2.2中所述,使用混合了六面体和四面体晶格的混合晶格。为了更好地观察流动边界层对叶轮壁和叶轮侧壁的影响,使用了密集的边界层网格。为了准确计算蜗壳壁面的速度梯度,壁面边界层如图1所示。3,网格总数为114万。
4.1.1 解释方法
对于时间项,分别在伪瞬态和时间瞬态两种状态下进行分析,湍流模型分别采用k-ωSST和k-ε模型。在压力-速度联动中,采用了耦合方法,SIMPLE或SIMPLEC是分别计算压力和速度的分离方法,在本研究中处理的离心泵分析中是近似的。
如图。图4和5示出了在垂直于离心泵的旋转轴线的截面中流速和速度矢量的大小。流体的速度从叶轮轮毂到叶尖增加,这是因为叶轮叶尖(tip)的角速度较大。此外,可以看出,由于网格是从墙壁垂直方向分层创建的,因此可以清楚地表示墙壁上出现的速度梯度,从而可以在墙壁上表示边界层。如图,6、叶轮旋转所产生的转速能量。


Fig.5FLUENT中的速度向量(伪瞬态)
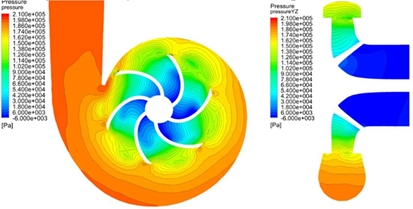
Fig.6FLUENT中的压力等值线(伪瞬态)
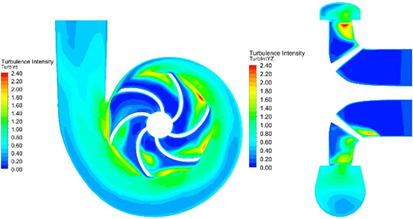
Fig.7FLUENT中的湍流强度等值线(伪瞬态)
4.3Time-Transient分析结果
离心泵是通过叶轮的旋转将能量施加到流体上,并将由蜗壳增加的流体的速度能转化为压力能的过程。()瞬态)流动分析可以被认为是一种合适的分析方法.然而,一般来说,包括时间项的流量分析需要大量的物理时间来执行分析。本研究中,对于1450rpm的单叶轮转速,时间间隔为0.0001s,进行异常状态分析显得相当大。如图10的压力分布,证实了由叶轮加速的流体通过横截面积扩大的蜗壳转化为压力能。预测出入口段压差为218kPa,比拟瞬态分析结果高出约7%。
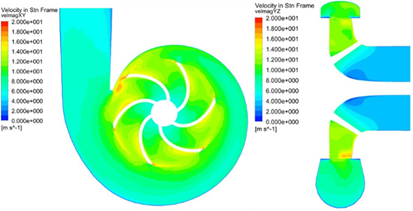
Fig.8FLUENT中的速度幅度等值线(瞬态)
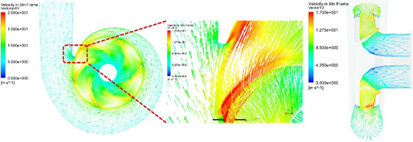
Fig.9FLUENT中的速度向量(瞬态)

Fig.10FLUENT中的压力等值线(瞬态)
如图10的压力分布,证实了由叶轮加速的流体通过横截面积扩大的蜗壳转化为压力能。预测出入口段压差为218kPa,比拟瞬态分析结果高出约7%。
1.FEM分析结果
基于FEM的流动分析概述用于分析的NFX版本是midasNFX2016R1版本,流动分析是在FLUENT分析中使用的相同形状模型上进行的。
5.1.1创建网格
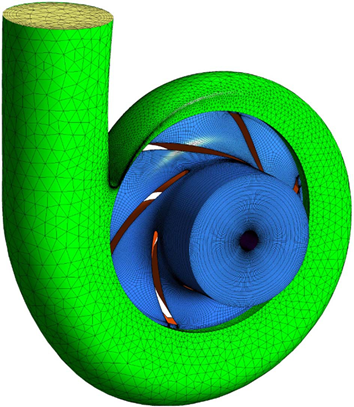
为了创建适用于基于FEM的NFX求解器的网格,使用四面体网格划分流动空间的方法,仅对关键区域(例如尖端外围、叶轮和蜗壳)进行播种,并使用所有节点作为首要因素。最终完成的网格如图所示。11,并且NFX的网格生成算法不支持边界层网格生成,所以无法在靠近墙壁的地方生成密集的边界层网格。对于墙,应用墙距离边界条件,这是一种通过为包括墙的单元的第一个节点距离分配适当的无量纲墙距离值来实现墙规则的方法。

Fig.11MeshforNFXsolver
5.1.1解释方法
至于时间,与FLUENT的情况一样,以两种类型进行分析:伪瞬态(在程序GUI选项中,指示稳态,但实际操作为伪瞬态形式)和时间瞬态状态,湍流模型分别使用了两种类型的k-ωSST和k-ε。至于压力-速度联动,由于NFX只提供了分离求解器算法,因此使用它进行分析。
5.1 分析结果
图12和13分别显示了在伪瞬态条件下垂直于旋转轴的横截面的流速大小和压力分布结果。图通过FLUENT预测。对比图4中的流速分布,可以看出NFX和FLUENT预测的流速分布相似,除了尖端附近的最大速度值不同。在压力分布的情况下,两个SW之间的压力也是。
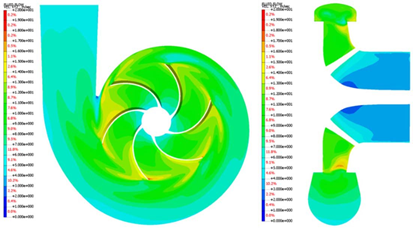
Fig.12NFX中的速度轮廓(伪瞬态)
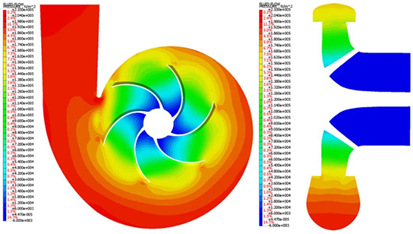
Fig.13NFX中的压力等值线(伪瞬态)
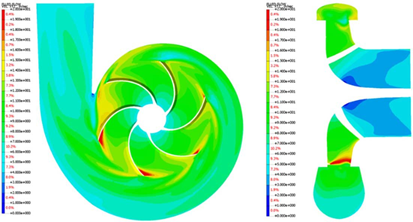
Fig.14NFX中的速度轮廓(瞬态)
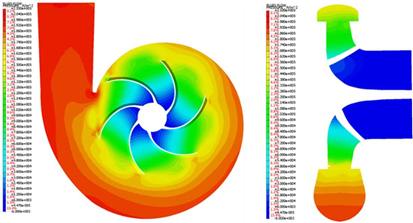
Fig.15NFX中的压力等值线(瞬态)
泡沫趋势被判断为处于相似水平,并且作为从NFX推导输入和输出部分之间的压力差的结果,在伪瞬态和时间瞬态分析中分别预测了207kPa和210kPa的压力上升.在FLUENT的情况下,输入和输出部分之间的压力差在伪瞬态和时间瞬态之间有大约15kPa的差异,但在NFX的情况下,有3kPa的差异,所以对于这个问题,NFX是否包含时间项而不是FLUENT。被认为对这个问题不太敏感在时间瞬态分析的情况下,分析以与FLUENT相同的时间间隔进行,0.0001秒。图14显示了1秒后的流速大小分布,预测叶轮叶尖附近的速度大于伪瞬态的速度。发现蜗壳内的流动并没有均匀地逸出,而是以弱涡流的形式离开蜗壳。湍流能量在叶轮叶尖的顶端产生,主要在蜗壳与叶轮的接触附近产生。在涡度的情况下,发现它主要发生在叶轮尖端的尖端。如图。如图15的压力分布所示,从叶轮接收动能的流体通过蜗壳可以看出压力进一步增加,可以确认在约0.4秒后压力差保持恒定。
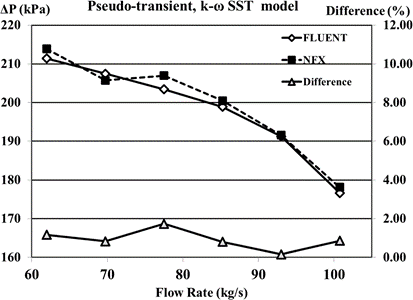
Fig.16入口和出口之间相对于流速的压差(伪瞬态)
在伪瞬态分析中,当流速为77.5kg/s时,FLUENT的最终压升为203kPa,比NFX的207kPa降低了1.9%。为了进一步评估泵的性能,当流量从62kg/s变为93kg/s时,计算每个流量的入口和出口段之间的压力差。通过此,根据流量变化的压力上升(压力流量图,P-Q图)曲线如图1所示。16、泵的性能可以通过P-Q图来判断。FLUENT和NFX都清楚地表明压差和流量成反比,但在NFX的情况下,当流量为69.75kg/s时,结果略微偏离了反比趋势。当流速为77.5kg/s或更低时,在计算Fluent和NFX时会出现一些数值振动。在未达到目标流量的非设计点,泵可能会振动,因为低流量可能会在吸入部分发生剥离。由于很难假设这种现象是与时间无关的物理现象,因此假设不考虑时间项的影响,因为稳态或伪瞬态不适用于低流速下的泵流量分析...在给定的流量范围内,FLUENT和NFX之间的ΔP差异在2%以内是正常的。在假设状态流的离心泵分析中,可以确认基于FEM的NFX和基于FVM的FLUENT的结果处于相似的水平。
在瞬态分析中,FLUENT的最终压升为218kPa,比NFX的210kPa高出3.8%。在FLUENT结果中,预计湍流能量低于NFX,叶轮叶尖附近的湍流能量较大。在涡度的情况下,NFX和Fluent都主要发生在叶轮的后部,并在不久后消失。可以确认,随着接近尖端,涡量增加,并且预测具有与NFX相同的趋势。在NFX的情况下,根据时间项处理方法,结果没有显着差异。但是,由于NFX缺乏生成边界层晶格的能力,因此可以看出应用湍流模型是有限制的受k-ωSST等壁格结构的影响很大。由此判断,使用对薄壁边界层的影响不太敏感的k-ε级湍流模型更适合NFX晶格系统。结果,判断为湍流模型的流动特性变化很小,因为NFX难以有效地实现壁边界层。FLUENT在压力-速度联动方法中采用了耦合求解器,这是因为在这个泵流量分析问题中,FLUENT无法通过分离求解器SIMPLE和SIMPLEC获得稳定的近似解。另一方面,NFX不提供耦合求解器,因此只能使用分离求解器解决问题。
这被认为是由于FEM和FVM在空间离散化技术上的差异,需要进行更严格的数值分析。首先,为了对两种数值分析方法进行严格的比较和分析,需要在同一网格系统中运行FLUENT和NFX求解器,直接比较两种CFD求解器的计算结果。但是,由于每个软件中可用的网格生成器的功能差异以及网格文件格式的兼容性问题,无法应用相同的网格。另一方面,如果使用相同的格子,针对一个求解器优化的格子可能不适用于另一个求解器,因此很难简单地使用相同的格子来比较两个求解器的结果。因此,在本研究中,对于具有不同离散化方法的两个求解器,为每个求解器使用适当的网格以确保分析过程中的收敛性和稳定性,并比较了不考虑网格敏感性的近似解。在数值分析中确保收敛性和稳定性的情况下,针对同一问题,通常收敛到相同水平的近似解,这可以被认为是SW之间的验证方法。由于无法使用相同的网格,两种求解器的计算结果在稳定性或收敛性方面可能存在细微差异,在实际计算结果中也得到了证实。在本研究中,考虑到网格导致的分析结果差异,通过改变流动条件对离心泵的整体性能进行了比较,重点是通过考虑每个SW的分析特性来提高收敛性和稳定性。




