midas应用之网格划分注意事项
网格划分的那些事
有限元分析(FEA,Finite Element Analysis):利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。还利用简单而又相互作用的元素,即单元,就可以用有限数量的未知量去逼近无限未知量的真实系统。
有限元分析包括前处理、分析、后处理
前处理:建立模型(几何-网格-材料/截面-边界-荷载)
分析:分析类型(静力、动力、线性、非线性)
后处理:结果查看及计算书整理
其中前处理占整个有限元分析70%-80%工作时长。

有限元分析模型包含节点、单元、边界条件和荷载条件。
节点决定模型的位置
单元决定形状和材料特性
边界条件决定连接状态
载荷决定受力情况
而网格划分是仿真分析中的重中之重。
网格分为结构化网格(Structured Mesh)和非结构化网格(Unstructured Mesh)
结构化网格
内部节点的Valence均为4的网格(内部节点的位相相同)
目标的限制
(1) 必须为由四条曲线组成的封闭区域
(2) 相对的两条曲线上有相同的节点数量

非结构化网格(
内部节点的Valence维持在3~5较好
对目标没有限制
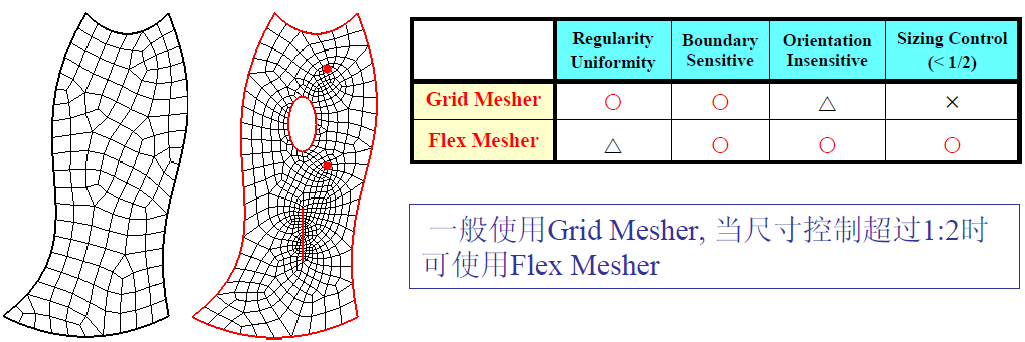
网格划分的对象是几何体,midas NFX针对不同几何形式和力学简化形式,提供多种单元模拟

针对不同单元类型,midas NFX提供自动,映射2种不同划分方法,也可以根据几何受力特点,提前对敏感位置布置种子。


在做网格划分时,即使网格划分成功,但质量太差,结果的精度也会受很大的影响
故在划分完后有一个很重要的步骤就是查看网格质量。
评定网格质量的常见六个参数
纵横比(Aspect Ratio)、歪扭角(SkewAngle)、翘曲(Warpage)、锥度(Taper)
雅克比比率(JacobianRatio)扭曲角(Twist)单元长度


[纵横比(AspectRatio)]
2D单元中的宽度和长度的比,或者是最长边和最短边的长度的比。例如,正方形的情况下,因为宽度和长度相等,所以值为1。形状越偏离正方形,纵横比就越小。值越接近1越理想。这对分析结果有重要影响;若值非常小,则很难得到正常的分析结果。评价应力为主时不要超过1/3,评价位移为主目的时不要超过1/5;非线性分析时,形状比的作用比非线性分析时更敏感。
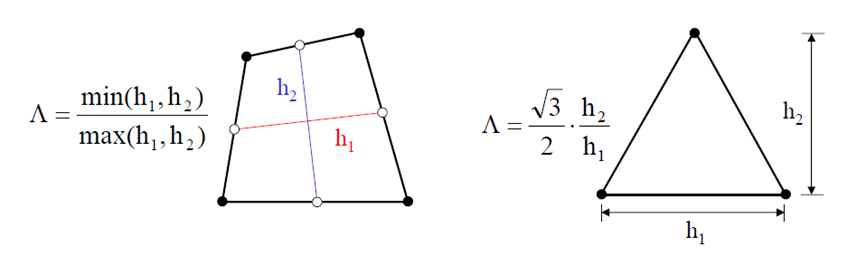
其值越接近1,说明网格质量越好
[歪扭角(SkewAngle)]
以角度测量形状偏离直角形状(90度)的程度。四边形的角是90度,所以歪扭角度为0,形状越偏离四边形值越大。就会从0度开始逐渐增大。实体单元的情况下,检查各面的歪扭角度,最小的值作为歪扭角。值越接近0越好。
 其值越接近0,说明网格质量越好
其值越接近0,说明网格质量越好
[翘曲(Warpage)]
评估偏离平面的程度。四边形2D单元的所有节点位于同一平面位置上时,这个值为0,偏离平面的程度越严重,值越大。实体单元的情况下,检查实体各四边形的翘曲值,最小的值作为翘曲值,值越接近0越好。这对分析结果有重要影响;若值非常大,则很难得到正常的分析结果。

四边形单元的四个节点偏离同一平面的程度(只使用于四边形单元)
•尤其要注意在两个曲面相连的位置的四边形单元
•翘曲比较明显的四边形单元应使用两个三角形单元来替换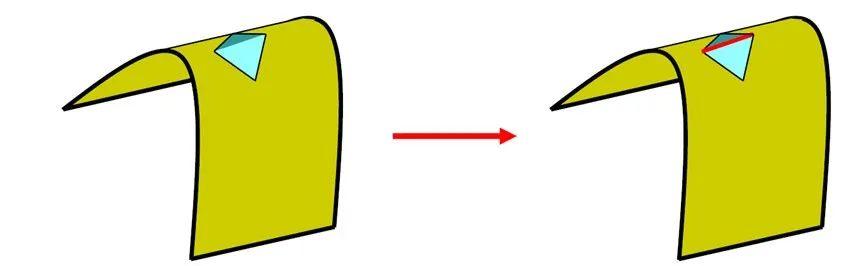
[锥度(Taper)]
按几何计算偏离四边形的程度。不适用于三角形单元。四边形的值为1,偏离四边形的程度越严重(越接近三角形形状),值越大。实体单元的情况下,检查各面的锥度,最小的值作为锥度,值越接近1越好。
用几何偏离(Geometric Deviation)表示四边形单元的变形程度. (只使用于四边形单元)

[雅克比比率(JacobianRatio)]
计算网格的各高斯积分点中的雅克比行列式后,最大的雅克比行列式和最小的雅克比行列式值的比就是雅克比比率。二维单元的情况下,雅克比行列式按投影到平面的单元计算,实体单元的情况下,直接计算雅克比行列式。如果在四边形单元不是凸的,就会出现负数值,将不能正常执行分析。如果三角形的每个中间节点都在三角形边的中点上。那么这个三角形的雅可比比率为1,下图所示为几种不同的雅可比值的三角形网格。
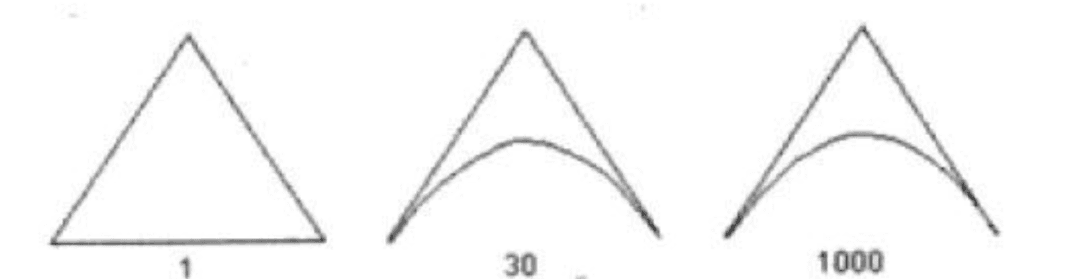
任何一个矩形单元或平行四边形单元,无论是否含有中间节点,其雅可比比率都为1,如果垂直一条边的方向向内或者向外移动这一条边上的中间节点,会加大加雅可比比率。下图所示为几种不同的雅可比比率的四边形网格。

满足以下两个条件的四边形单元所生成的六面体单元雅可比比率为1:所有对边都相互平行,任何边上的中间节点都位于两个角点的中间位置。
[扭曲角(Twist)]
表示实体单元中相对的两个面的扭转程度。
小结:
纵横比(Aspect Ratio),或者叫长宽比(软件默认值一般为15)
歪扭角(Skew Angle),(软件默认值一般为45)
翘曲(Warpage),(不同软件定义有所不同,NFX默认值一般为25)
锥度(Taper),(软件默认值一般为0.25~0.5)
雅可比比率(Jacobian Ratio),(软件默认值一般为0.7,或者大于0)
扭曲角(Twist Angle),(软件默认值一般为30)
单元长度(Element Length),(软件默认值一般为最小长度为0.1mm,最大为100mm)
trip网格划分参考:
事先建立建模计划
•越是复杂的部分,越要努力寻找复合规律的方案
•用单元数量粗算单元尺寸,使用下列公式粗略计算单元尺寸

•几何形状、刚度(材料/厚度)以及荷载有变化的位置、应力集中位置应细分网格。
•分析后检查下列各项,误差较大的位置要细分
a:单元应力的连续性
比较相邻单元的应力值的差值
b:应力偏差(Stress Deviation)
节点上的单元节点应力和节点平均应力的差值的较大值
当以上差值与其中的最大应力的比值较大时,需要将该位置重新细分
•不同类型的单元连接时,要注意自由度的耦合(未考虑接触边界情况)
a:板单元
因为板单元没有绕单元坐标系z轴的旋转自由度(Drilling DOF), 所以当梁与板的连接如果诱发板单元绕单元z轴的旋转的话,连接位置在某个方向将成为铰接。
b:实体单元
因为实体单元没有旋转自由度,所以与板单元相连时有可能在某个方向成铰。

•使用最小的标准单元建模
尽量先建立最小的标准单元或对称单元,然后利用复 制和镜像功能
•尽量使用结构化网格→ 注意倾斜角(Skew Angle)
•要控制网格密度,不要建立过多的单元
→ 只细分重要的部位
•检查自由边和自由面,确认单元之间的连接
•查看是否能由低次单元扩展为高次单元,(扩展后可删除低次单元)





基于仿真分析对于使用者要求,上手困难,学习成本高等诟病,秉承“用技术创造幸福”的理念,2014年迈达斯公司与美国佛罗里达大学KIM Nam-Ho教授联合研究,基于隐式边界法,开发了无网格划分设计软件MeshFree,并于2018年面市。


测评结果





